Семинар ДООнк Использование приема моделирования на уроках математики при решении текстовых и логических задач

Груздева Ольга Владимировна ID-z022

Все мы хотим, чтобы наши дети были смышлёными, догадливыми, сообразительными, умными. А умён тот, кто умеет мыслить. И хотя все психологи сходятся во мнении, что мышление человека – это высшая форма его познавательной деятельности, тем не менее, их взгляды на процесс мышления отличаются. Одни из них считают процесс мышления исключительно продуктивным, когда в результате работы получается новое решение, новая идея (С.Л. Рубинштейн), другие же включают в него и репродуктивные (воспроизводящие имеющиеся у человека знания) этапы (П.Я. Гальперин). «Искание и открытие нового» - действительно творческий, познавательный процесс. И надо научить ребёнка находить своё оригинальное решение, где готовые алгоритмы непригодны. Задача учителя – помочь ребёнку научиться мыслить. А значит надо создать такую ситуацию на уроке, когда сам ребёнок захотел бы мыслить, вооружив учащихся необходимым средством для решения математических задач - моделированием. Модель, выступая как продукт мыслительного анализа, затем сама становится особым средством мышления ученика. С первого класса наши учащиеся постепенно осваивают разные виды моделирования математических отношений: чертежи, различные схемы, которые помогают им в работе с задачами. В 3 классе дети осваивают способ моделирования с помощью специальных знаковых средств - «окошки со стрелками». В каждое «окошко» вписывается значение величины, если оно известно. А между взаимосвязанными величинами находятся стрелки, направление которых указывает на значение большей величины при разностном или кратном отношениях. Если величины связаны друг с другом отношением равенства, то они соединяются двумя линиями, символизирующими знак =. Также на этих схемах можно показать отношение целого и частей, когда стрелочки от всех частей соединяются в одну стрелку, направленную к целому. Каждое отношение указывается одной стрелкой (возможно, раздвоенной, тройной и т.п.). Члены отношения определяются только своим положением относительно стрелки. Выбор действия при решении задачи определяется положением неизвестного относительно стрелки. Помимо содержательного смысла, т.е. что ищется – часть или целое, большая или меньшая величина при кратном или разностном отношении и т.п., есть и формальные признаки действий. Величина, стоящая у острия стрелки, всегда находится сложением или умножением, а все остальные – вычитанием или делением. Предлагаю вниманию конспект урока по математике для 3 класса на тему: “Работа с текстовыми задачами. Выделение отношений в тексте задач и фиксация их схемой». (Авторы учебника: Давыдов В.В., Горбов С.Ф. и др.)

На этот момент обучения при работе с текстовыми задачами используются только четыре типа отношений – разностное отношение, отношение кратности, отношение целого и частей, отношение между целым и частями в случае равных частей.

Основной целью работы с текстовыми задачами является формирование у учащихся рациональных способов анализа текстов, т.е. определение математической структуры задачи (описываемых в тексте величин и связывающих их отношений), её моделирование с помощью знаковых средств.

1. Открываем с.86. Прочитайте про себя № 743 (2).

Учащиеся читают задание: постройте схему и решите задачу.

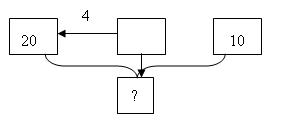
Бабушка посадила 20 луковиц тюльпанов, а внучка – в 4 раза меньше. После этого у них осталось 10 луковиц. Сколько луковиц тюльпанов у них было сначала?

У. Для чего надо построить схему?

Д. Чтобы выделить величины и отношения, которые их связывают.

Задача читается вслух.

У. Сколько величин в этой задаче?

Д. Четыре: количество луковиц у бабушки, количество луковиц у внучки, количество оставшихся луковиц, количество луковиц, которые были у них сначала.

У. Сколько «окошек» будет в схеме?

Д. Сколько величин, столько и «окошек» - 4.

У. А какие отношения между величинами?

Д. Отношение кратности и отношение целого, состоящего из 3-х частей.

У. Выполните в тетрадях заготовку схемы (расстановка пустых «окошечек»).

А теперь читаем задачу по частям и вставляем в схему известные величины, обозначаем искомую величину вопросительным знаком, указываем отношения между величинами. Два ученика работают у доски: один из них медленно читает задачу, другой заполняет «окошки». Остальные ребята работают самостоятельно. После выполнения идёт проверка работы учащихся.

У. Кто может, не глядя в учебник, проговорить условие задачи (с опорой на схему)? Выслушиваются ответы детей. По ходу ответа учащиеся что-то дополняют, уточняют, спрашивают, если возникает необходимость.

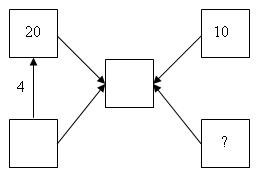
У. В другом классе мальчик предложил вот такую схему к этой задаче. Вы согласны с ним?

Д. Нет. Эта схема не подходит к нашей задаче.

У.Чем отличаются эти схемы?

Д. В нашей схеме неизвестное является целым, а здесь – частью.

Д. Целое должно состоять из 3-х частей, а тут – из 2-х частей.

Д. В этой схеме целое, составленное из 2-х частей, по-новому разбивается на две части.

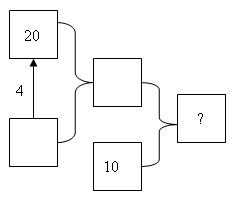
У. А другая схема?

Д. А эта схема подходит.

Далее учащиеся вместе с учителем анализируют данную схему. Учитель последовательно указывает рукой на каждое «окошечко» и спрашивает детей: «Про что это?» Ученики отвечают.

Д. Это - количество луковиц, которые посадила внучка.

Д. Это – сколько луковиц они посадили вместе.

Д. Это – сколько луковиц у них было сначала.

У. Схемы разные, а что будет одинаковым?

Д. Ответ.

У. Запишите решение к каждой схеме.

К двум схемам записывается решение.

1) 20 : 4 = 5 (лук.) - посадила внучка	2) 20 + 5 + 10 = 35 (лук.)
1) 20 : 4 = 5(лук.) - посадила внучка	2) 5 + 20 = 25(лук.) – посадили вместе	3) 25 + 10 = 35(лук.)

По схемам проверяем решение. Учитель вновь проводит рукой от одного «окошка» к другому и спрашивает: «Здесь сколько?» Ответ записывает цветным мелом в каждое «окошечко».

2. У. Запишите ту схему, которая не подошла.

У. Измените сюжет задачи под эту схему.

Дети составляют много задач под эту схему. Вот некоторые варианты задач, предлагаемых детьми.

Д. Бабушка посадила 20 луковиц тюльпанов, а внучка – в 4 раза меньше. Из всех луковиц проросли только 10. Сколько луковиц не проросли?

Д. Бабушка посадила 20 луковиц тюльпанов, а внучка – в 4 раза меньше. Весной из этих луковиц выросли тюльпаны красного и жёлтого цвета. Красных было 10. Сколько жёлтых тюльпанов выросло?

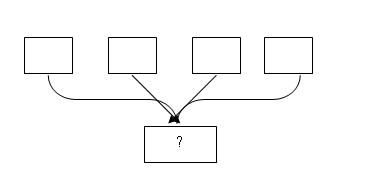
У. Я предлагаю схему к этим задачам записать по-другому. Вот так.

Д. Эта схема не подходит. В ней неизвестно целое, которое состоит их 4-х частей.

Д. В наших задачах целое состоит из 2-х частей. С одной стороны это целое состоит из количества луковиц, которые посадили бабушка и внучка. С другой стороны это же целое разбивается на другие части – количество проросших луковиц и тех, которые не выросли, или количество жёлтых и количество красных тюльпанов.

Д. В нашей задаче мы ищем значение части.

У. Убедили. Сейчас решите каждый свою задачу.

1) 20 : 4 = 5 (лук.) – посадила внучка

2) 20 + 5 = 25 (лук.) – посадили вместе

3) 25 – 10 = 15 (лук.) – не проросли

3. У. Прочитайте задачу, записанную на доске. (Дети читают про себя, затем один ученик читает вслух).

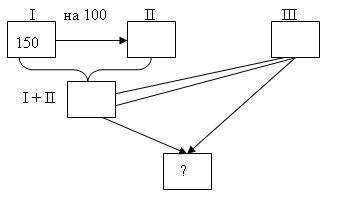
В библиотеке стояли три шкафа. В одном шкафу было 150 книг, а во втором – на 100 книг больше, чем в первом. В третьем шкафу было столько книг, сколько в первом и втором шкафах вместе. Сколько книг было в библиотеке?

У. Покажите на пальцах, сколько величин в этой задаче, т.е. сколько «окошек» будет в схеме. Мнения детей расходятся: кто-то показывает 4, кто-то 3, кто-то 5 пальцев.

У. Давайте разберёмся, кто же из нас прав. Кто будет работать у доски со схемой? А кто будет нам с места медленно читать задачу? (Один ученик выходит к доске, а другой с места медленно вслух читает задачу).

В процессе работы выясняется, что первое «окошко» - количество книг в I шкафу, второе – количество книг во II шкафу, третье –количество книг в III шкафу. В первое «окошко» вставляется известная величина.

У. Какие величины связаны между собой и каким отношением?

Д. Первая и вторая величины связаны разностным отношением. Во втором шкафу книг было больше, значит, стрелка направлена остриём ко II величине. Над стрелкой запишем значение разности (100 книг).

У. Читаем следующее предложение.

Д. В третьем шкафу было столько книг, сколько в первом и втором шкафах вместе.

У. А как это? Какое здесь отношение? Целого и частей?

Д. Нет. Это отношение равенства.

У. Между какими величинами?

Д. Надо нарисовать «окошко», в котором будет величина I+II и от него провести равенство к третьей величине.

У. А узнать надо что?

Д. Целое (I+II+III).

У. Доделайте схему.

Далее учащиеся самостоятельно решают задачу, заполняя постепенно каждое «окошко» схемы. Найденные величины записываются в «окошки» другим цветом.

Затем решение проверяется:

1) 150+100=250 (книг) – во II шкафу	2) 150+250=400 (книг) – в 2-х шкафах	3) 400+400=800 (книг)
Значение вписывается во II «окошко»	Значение вписывается в I+II «окошко» и в III «окно»

У. Кто последнее действие записал не так?

Д. 400*2=800 (книг)

4. Перечертите схему.

У. Схема коротенькая. Придумать задачу несложно.

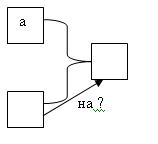
Д. У Пети и у Маши были шарики. У Маши «а» шариков. На сколько шариков меньше было у Пети, чем у них было вместе.

У. Думайте. Может задача и не решается. Кому кажется, что данных не хватает? Можно я вам ответ нарисую.

О - __ = __

Дети пытаются как-то объяснить решение.

У. Дома подумайте и придумайте лучшее объяснение.