Семинар ДООМ: Урок по теме « Теорема Пифагора».
Проба (обсуждение | вклад) |
Проба (обсуждение | вклад) |
||
| Строка 49: | Строка 49: | ||
1) Задача. Найти длину лестницы,[[Изображение:Lectn.jpg|thumb|left| Длину лестницы мы сможем найти после изучения теоремы Пифагора]], | 1) Задача. Найти длину лестницы,[[Изображение:Lectn.jpg|thumb|left| Длину лестницы мы сможем найти после изучения теоремы Пифагора]], | ||
приставленной к дому, если один её конец находится на расстоянии 3 м от дома, | приставленной к дому, если один её конец находится на расстоянии 3 м от дома, | ||
| + | |||
а другой находится на стыке стены и крыши. | а другой находится на стыке стены и крыши. | ||
| + | |||
Высота дома 4 м. | Высота дома 4 м. | ||
| Строка 65: | Строка 67: | ||
Докажем, что с² = а² + b² | Докажем, что с² = а² + b² | ||
| − | Достроим треугольник до квадрата со стороной a + b. Площадь S этого квадрата равна (а + b)². С другой стороны, этот квадрат составлен из четырёх равных прямоугольных треугольников, площадь каждого из которых равна ½ab , и квадрата со стороной с, поэтому S = 4 ∙ ½ab + c² = 2ab +c² | + | Достроим треугольник до квадрата со стороной a + b. Площадь S этого квадрата равна (а + b)². |
| + | |||
| + | С другой стороны, этот квадрат составлен из четырёх равных прямоугольных треугольников,[[Изображение:Dokazat.jpg|right]] | ||
| + | |||
| + | площадь каждого из которых равна ½ab , и квадрата со стороной с, | ||
| + | |||
| + | поэтому S = 4 ∙ ½ab + c² = 2ab +c² | ||
| − | Таким образом, (a + b)² = 2ab + c², | + | Таким образом, (a + b)² = 2ab + c², Откуда c² = a² + b² |
| − | + | '''Теорема доказана.''' | |
| − | ''' | + | |
| − | Теорема доказана.''' | + | |
Версия 22:59, 5 декабря 2009
Заголовок ссылкиУрок в 8 классе по теме « Теорема Пифагора».
Автор Рыскалкина Наталия Васильевна
Цели урока:
1. Научить доказывать теорему Пифагора.
2. Научить применять теорему Пифагора к решению задач.
3. Развитие интереса к математике через ознакомление с историческим материалом.
Ход урока.
I. Вступительное слово учителя.
Да, путь познания не гладок.
Но знаем мы со школьных лет,
Загадок больше, чем разгадок,
И поискам предела нет!
На радужной узрел я оболочке
Бегущие квадратики, кружочки,
Вселенной опрокинутый узор,
И вспыхнуло в мелькании сквозь строчки
Пылающее имя – Пифагор!
Учитель формулирует тему и цели урока.
II. Подготовительная работа.
-Как называют стороны прямоугольного треугольника?
-Чему равна площадь прямоугольного треугольника?
-Чему равна площадь квадрата?
-Чему равен квадрат суммы двух выражений?
III. Объяснение нового материала.
1) Задача. Найти длину лестницы,,приставленной к дому, если один её конец находится на расстоянии 3 м от дома,
а другой находится на стыке стены и крыши.
Высота дома 4 м.
2) О теореме Пифагора. Теорема Пифагора – одна из самых главных теорем геометрии. Значение её состоит в том, что из неё или с её помощью можно вывести большинство теорем геометрии и решить множество задач.
3) Формулировка и доказательство теоремы Пифагора.
Теорема: В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
Доказательство:
Рассмотрим прямоугольный треугольник с катетами а, b и гипотенузой с.
Докажем, что с² = а² + b²
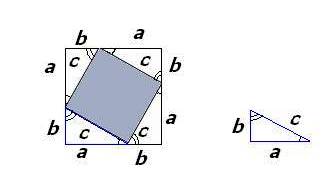
Достроим треугольник до квадрата со стороной a + b. Площадь S этого квадрата равна (а + b)².
С другой стороны, этот квадрат составлен из четырёх равных прямоугольных треугольников,площадь каждого из которых равна ½ab , и квадрата со стороной с,
поэтому S = 4 ∙ ½ab + c² = 2ab +c²
Таким образом, (a + b)² = 2ab + c², Откуда c² = a² + b²
Теорема доказана.