Семинар ДООМ: Ромб, свойство диагоналей ромба
м («Ромб, свойство диагоналей ромба» переименована в «Семинар ДООМ: Ромб, свойство диагоналей ромба») |
Версия 06:54, 7 декабря 2009
Маклецова Ирина Анатольевна Аб-солютики IDm023
Цель урока:
1. Систематизировать, обобщить знания учащихся. 2. Ввести свойство диагоналей ромба. 3. Развить творческое отношение к делу.
План урока:
1. Организационный момент. 2. Повторение. 2.1. Теоретический материал. 2.2. Работа по готовым чертежам. 3. Новый материал. 3.1. Построение чертежа 3.2. Перечисление свойств. 3.3. Работа в парах. 3.4. Самостоятельная работа. 3.5. Разбор и доказательство теоремы. 4. Закрепление нового материала. 5. Работа по готовым чертежам. 6. Подведение итогов. 7. Задание на дом:
Ход урока:
1. Организационный момент. 2. Повторение: 1. Теоретического материала: А) Дать определение равнобедренного треугольника. Б) Сформулировать теорему о сумме углов в треугольнике. В) Дать определение медианы треугольника. Г) Дать определение высоты треугольника. Д) Дать определение биссектрисы треугольника. Е) Сформулировать свойство медианы равнобедренного треугольника.
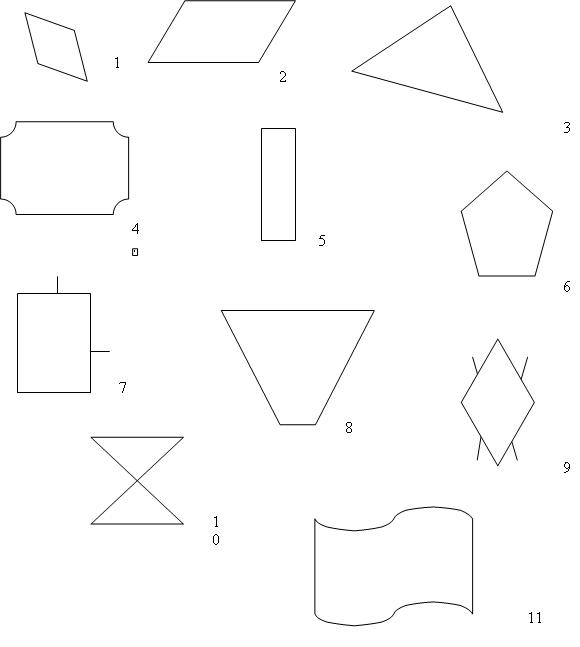
2. Работа по готовым чертежам.
•Назовите фигуры, у которых противолежащие стороны параллельны. (1, 2, 4, 5, 7, 8, 9, 10, 11) •Назовите рисунки на которых изображены четырехугольники. (1, 2, 5, 7, 8) •Почему фигура 10 не является четырехугольником? (есть пересечения) •Назовите рисунки на которых изображены четырехугольники, у которых противолежащие стороны параллельны. (1, 2 , 5, 7)
3. Новый материал. 1. Начертите в тетрадях параллелограмм, у которого все стороны равны. Проведите диагонали, точку их пересечения обозначьте через О.
2. Перечислите свойства, которыми обладает параллелограмм: угол А = угол С, угол В = угол D AD = DC, AB = CD; BD пересекается AC = O, AO = OC, BO = OD.
3. Работа в парах: Раздать на каждую парту карточку. а) Проверьте параллельность сторон, измерить все стороны фигуры. б) Чем интересна эта фигура? (все стороны равны) в) Какая фигура называется ромбом? (параллелограмм у которого все стороны равны называется ромбом)
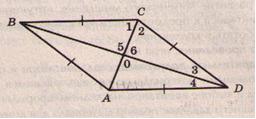
4. Самостоятельная работа 1 ряд - измеряет угол 1 и угол 2, делает вывод; (угол 1 = угол 2, значит СА – биссектриса треугольника ВСD) 2 ряд - измеряет угол 3 и угол 4, делает вывод; (угол 3 = угол 4, значит BD – биссектриса треугольника СDA) 3 ряд - измеряет угол 5 и угол 6, делает вывод; (угол 5 = угол 6 = 90, значит BD перпендикулярно AC) Общий вывод: диагонали ромба взаимно перпендикулярны и являются биссектрисами его углов. Но это нужно не утверждать, а доказать.
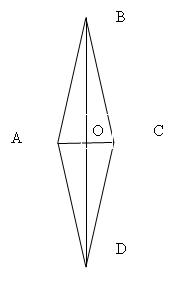
5. Разбор и доказательство теоремы. Теорема: Диагонали ромба взаимно перпендикулярны и являются биссектрисами его углов.
Дано: АВСD – ромб, BD пересекается AC = O. Доказать: что BD перпендикулярна AC, и каждая диагональ делит соответствующие углы ромба пополам например, что угол ВАС = углу DАС. Доказательство: 1)АB = АD по определению ромба треугольник ВАD равнобедренный; 2)так как ромб – параллелограмм, его диагональ пересекаются и делятся пополам; 3)АО – медиана равнобедренного ВАD; 4)АО – высота и биссектриса; 5)поэтому BD перпендикулярно AC и треугольник ВАС = треугольник DАС. Теорема доказана.
4. Закрепление нового материала. Задача 1. АВСD – ромб, угол DАВ = 100. Определите углы треугольника АОD. (50, 90, 40) Задача 2. Найдите углы ромба, в котором одна диагональ равна стороне.
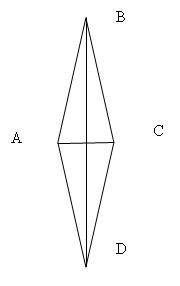
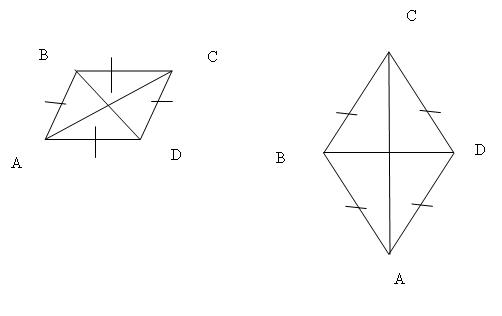
5. Работа по готовым чертежам. Перечислите свойства, которыми обладают отрезки АC и BD.
6. Подведение итогов. 7. Задание на дом: стр. 87, п. 55 (доказательство теоремы); стр. 99 № 35.