Семинар ДООМ Поверхности геометрических фигур

Материал из ТолВИКИ
(Различия между версиями)
Перейти к: навигация, поиск
 
(не показаны 22 промежуточные версии 1 участника)
Строка 1: Строка 1:
−
'''Тема урока:''' Урок одной формулы
+
'''Участник:''' Молдагалиева Дамира Ароновна,IDm063
 +
 
 +
'''Тема урока:''' Поверхности  геометрических фигур
 +
 
 +
'''Класс:'''11
  
 
'''Цели:'''
 
'''Цели:'''
 +
 
1.Систематизация формул вычисления поверхностей всех геометрических фигур,изученных в школе.
 
1.Систематизация формул вычисления поверхностей всех геометрических фигур,изученных в школе.
  
−
2.
+
2.тренировать способность: к анализу, сравнению, выявлению существенных свойств;  развитие навыков и умений работы с программой Star Board.
  
−
3.
+
3. воспитание информационной культуры учащихся, внимательности, аккуратности, дисциплинированности; умения работать в группах.  
  
 
'''Подготовка к уроку:'''
 
'''Подготовка к уроку:'''
Строка 12: Строка 17:
 
1)интерактивная доска
 
1)интерактивная доска
  
−
2)проектор
+
2)проектор
  
−
3)notebook с программой Star Board.
+
3)notebook с программным  обеспечением  Star Board.
  
 
4)компьютерный класс.
 
4)компьютерный класс.
  
−
'''Запись на слайде:''' Природа говорит языком математики, буквы этого языка-круги, треугольники и иные математические фигуры. Галилей.
+
18).'''Запись на слайде:''' Природа говорит языком математики, буквы этого языка-круги, треугольники и иные математические фигуры. Галилей.
  
  
Строка 25: Строка 30:
 
'''1. Организационный момент.'''
 
'''1. Организационный момент.'''
  
−
Проверка установки презентации  в каждом компьютере для индивидульных работ учащихся в режиме интерактивной доски  Star Board.
+
Проверка учительской презентации  в каждом компьютере для работ учащихся в режиме интерактивной доски  Star Board.
  
 
'''2.Устная работа.'''
 
'''2.Устная работа.'''
Строка 41: Строка 46:
 
'''3.'''Целью сегодняшнего урока является систематизация формул вычисления поверхностей всех геометрических фигур, изученных нами. Оказывается, достаточно отчетливо помнить одну основную формулу-формулу площади прямоугольника, чтобы вычислить площадь любой поверхности.  
 
'''3.'''Целью сегодняшнего урока является систематизация формул вычисления поверхностей всех геометрических фигур, изученных нами. Оказывается, достаточно отчетливо помнить одну основную формулу-формулу площади прямоугольника, чтобы вычислить площадь любой поверхности.  
  
−
Два ряда квадратных единиц по 6 в ряду:
+
Учащиеся парами садятся за компьютер, где открывают программу POWER point c презентацией по теме, и задачи в чертежах сопровождают решениями. После выполнения всех заданий учащиеся имеют возможность продемонстрировать свои презентации в режиме интерактивной доски.Здесь же учащиеся, сидящие за персональными компьютерами имеют возможность, при наличии ошибок, сразу же исправить их.
−
Площадь АВСД  S=ab        (1)
+
−
Квадрат По формуле (1) имеем S=a a  =  a2
+
−
Параллелограмм  Отрезаем  АВК и ставим его вместо  DCN. Получаем прямоугольник ВСNК .По формуле (1) имеем: S=ВС  ВК= ab.
+
−
Ромб.       Опять используем формулу (1). Площадь ромба равна половине площади прямоугольника. По формуле  (1) имеем  S=dd/2, где dd- диагонали
+
  
−
Прямоугольный треугольник.    По формуле(1) S=1/2 ab 
 
  
−
   Косоугольный треугольник.    S=1/2 S параллелограмма, S=1/2 ah.
+
'''Прямоугольник.'''Два ряда квадратных единиц по 6 в ряду:  Площадь АВСД   S=ab    (1)
  
−
S= a2    /4, h=a /2.
+
'''Квадрат''' По формуле (1)  S=a<sup>2</sup>;
  
−
Трапеция.         Сумма двух треугольников с общей высотой.  S=1/2 (AD+BC) /h.
+
'''Параллелограмм.'''  Отрезаем  АВК и ставим его вместо  DCN. Получаем прямоугольник ВСNК .По формуле (1) имеем: S=ВС * ВК= ab.
  
−
S=1/2 ( a+b) /h.
+
'''Ромб.'''  Опять используем формулу (1). Площадь ромба равна половине площади прямоугольника. По формуле  (1) имеем
 +
S= d<sub>1</sub>d<sub>2</sub>/2где d<sub>1</sub>,d<sub>2</sub>- диагонали
  
−
Правильный многоугольник.
+
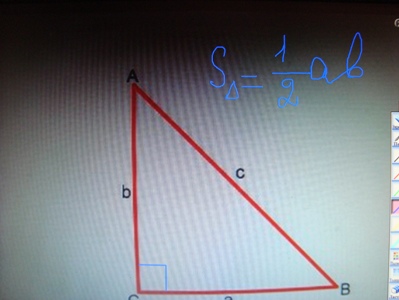
'''Прямоугольный треугольник.'''    По формуле(1) S=1/2 ab 
  
−
Площадь  SABCDEF =1/2 PABCDEF  r, где r-    радиус вписанной окружности.
+
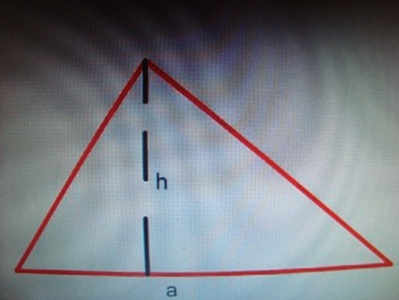
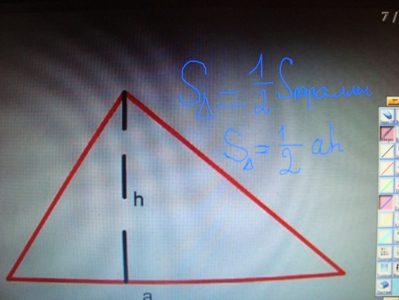
''' Произвольный треугольник.'''    S=1/2S<sub>параллелограмма</sub>, S<sub>треуг.</sub>=1/2 ah.
  
−
При =3 имеем случай, т.е. вычисляем SABC=1/2 PABC ОК, SABC =P  r.
+
'''Трапеция.''' Сумма двух треугольников с общей высотой.  S<sub>трап</sub>=1/2 (AD+BC)*h.
  
−
DК=в sin a,  SABCD= a в sin a, SADК= 1/2 a в sin a.
+
S<sub>трап</sub>=1/2 ( a+b)*h.
  
 +
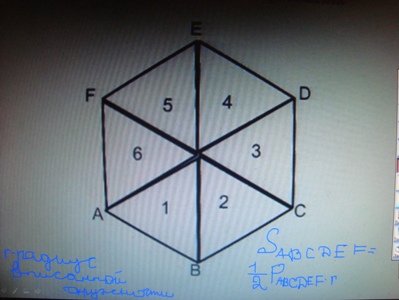
'''Правильный многоугольник.'''
  
−
SAВС= 1/2 a в sin С,     
+
S<sub>ABCDEF</sub> =1/2 P<sub>ABCDEF</sub> * r, где r-   радиус вписанной окружности.
  
−
По теореме синусов имеем: a /sin A = b/ sin В, b= a sin В/ sin A,   S=1/2 a2 sin В sin С/ sin A.
+
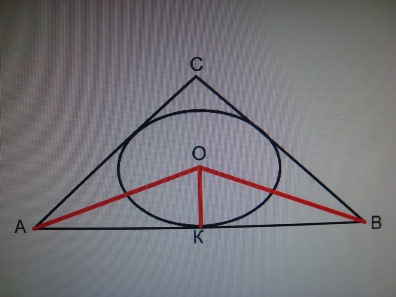
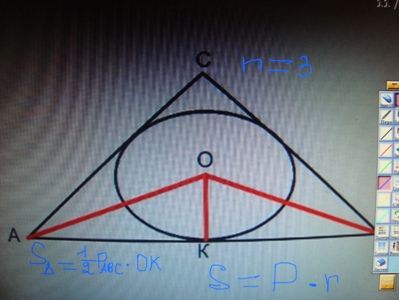
'''Вписанная окружность.'''При n=3 имеем случай, т.е. вычисляем  S<sub>ABC</sub>=1/2Р<sub>ABC</sub> * ОК, S<sub>ABC</sub>=P * r.
  
−
Пирамида (правильная n-угольная).
+
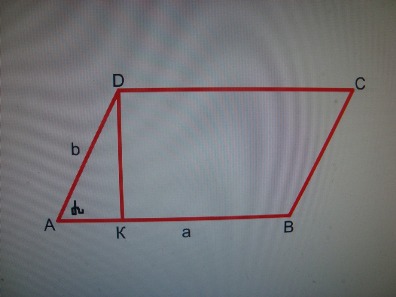
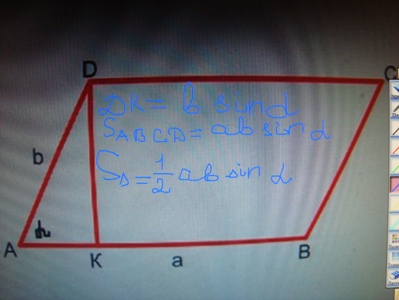
'''Параллелограмм.'''DК=в sin a,  S<sub>ABCD</sub>= a b sin a, S<sub>ADК</sub>= 1/2 a b sin a.
  
−
S бок. пир =1/2 АВ * SК, где  SК-апофема.
 
  
−
Призма (параллелепипед)
+
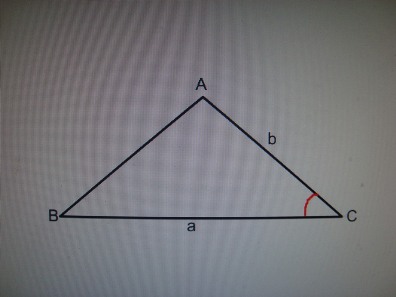
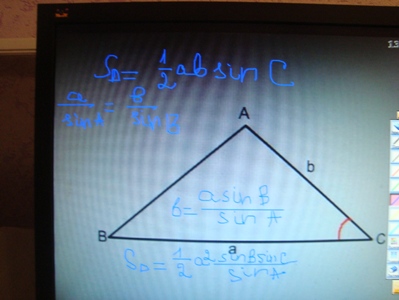
'''Треугольник.'''S<sub>AВС</sub>= 1/2 a b sin С,   
  
−
Цилиндр.
+
По теореме синусов имеем: a /sin A = b/ sin В, b= a sin В/ sin A,  S<sub>AВС</sub>=1/2 a<sup>2</sup> sin В sin С/ sin A.
−
Развертка боковой поверхности-прямоугольник  АВСD.  По формуле (1) имеем:  
+
  
−
Шаровой пояс.
+
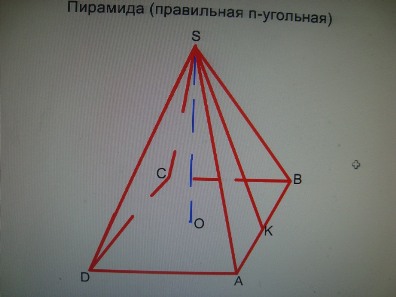
'''Пирамида''' (правильная n-угольная).
  
−
В математике часто используем предельные переходы. Если радиус кривизны сферы стремится к бесконечности, а высота шарового слоя стремится к нулю, то шаровой слой принимается за цилиндр, оставаясь все- таки шаровым слоем. Высота слоя  H.
+
S <sub>бок. пир</sub>=1/2 АВ * SК*n=1/2 АВ * n*SК=1/2Р<sub>АВСD</sub>*SК, где  SК-апофема.
−
H=2R.Секущие плоскости ОК=h можно расположить так, что образуется шаровой сегмент или целый шар.                S =2пRh, где  R-радиус большого круга сферы, h-высота сегмента.  S=2пR2R=4п R.
+
  
−
Конус.
+
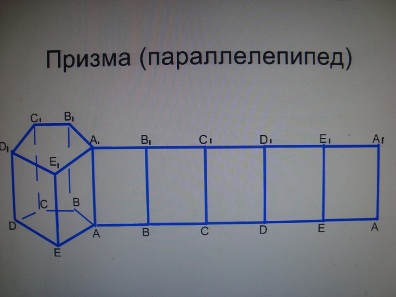
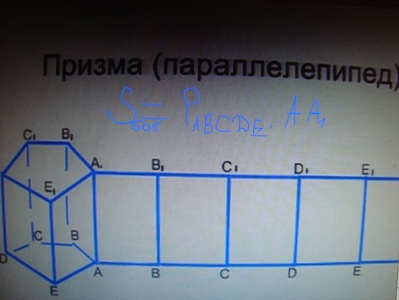
'''Призма (параллелепипед)'''
  
−
Усеченный конус.
+
S <sub>бок</sub>=Р<sub>АВСDЕ</sub>*АА<sub>1</sub>.
 +
 
 +
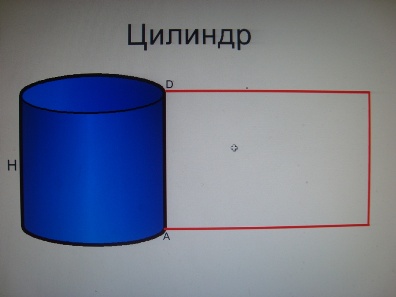
'''Цилиндр.'''
 +
 
 +
Развертка боковой поверхности-прямоугольник  АВСD.  По формуле (1) имеем:
 +
 
 +
S<sub>бок.цил</sub>=СН;  S<sub>бок.цил</sub>=2пRН
 +
 +
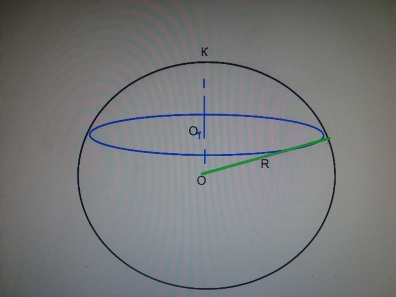
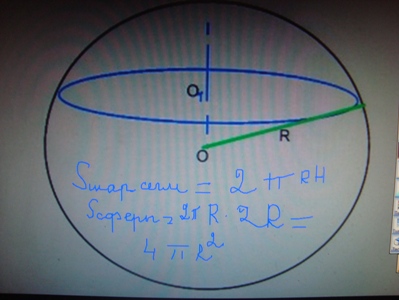
'''Шаровой пояс.'''
 +
 
 +
В математике часто используем предельные переходы. Если радиус кривизны сферы стремится к бесконечности, а высота шарового слоя стремится к нулю, то шаровой слой принимается за цилиндр, оставаясь все- таки шаровым слоем. Высота слоя H.H=2R. Секущие плоскости ОК=h можно расположить так, что образуется шаровой сегмент или целый шар.S<sub>шар.сег</sub>=2пRh, где R-радиус большого круга сферы, h-высота сегмента.S<сферы</sub>=2пR*2R=4пR<sup>2</sup>
 +
H=2R.Секущие плоскости ОК=h можно расположить так, что образуется шаровой сегмент или целый шар.  S =2пRh,  где  R-радиус большого круга сферы, h-высота сегмента.  S=2пR2R=4пR<sup>2</sup>.
 +
 
 +
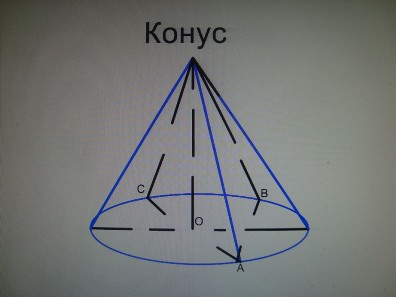
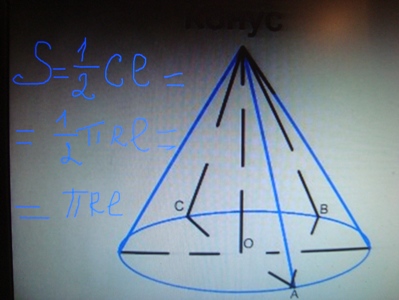
'''Конус.'''
 +
 
 +
S<sub>бок.кон</sub>=limS<sub>бок.пир</sub>=1/2Cl=1/2пRl.
 +
 
 +
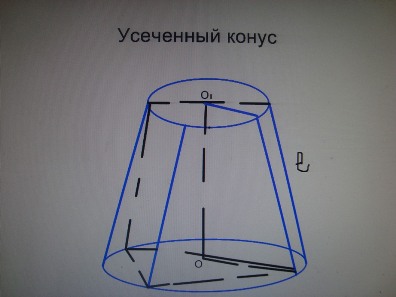
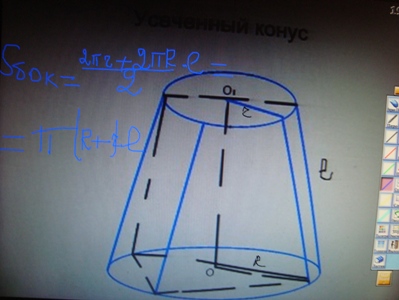
'''Усеченный конус.'''
 +
 
 +
S<sub>бок.ус.кон</sub>=limS<sub>бок.ус.пир</sub>,  S<sub>бок.ус.кон</sub>=1/2(2пr+2пR)*l=п(R+r)*l.
 +
 
 +
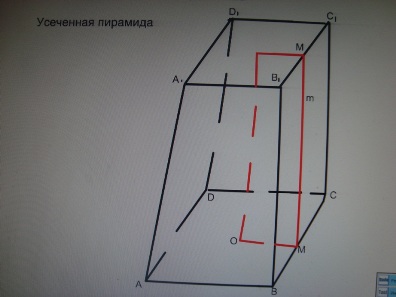
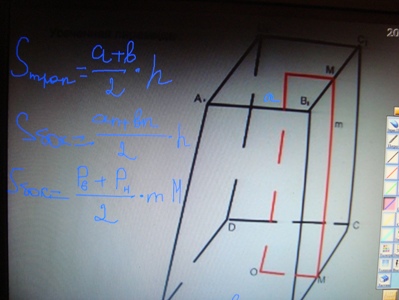
'''Усеченная пирамида.'''
 +
 
 +
S<sub>трап.</sub>=1/2(а+b)*h,
 +
 
 +
S<sub>бок</sub>= 1/2(аn+bn)*h,
 +
 
 +
S<sub>бок</sub>=1/2(Р<sub>в</sub>+Р<sub>н</sub>)*mМ.
  
−
Усеченная пирамида.
 
  
 
{| border=1
 
{| border=1
Строка 97: Строка 122:
 
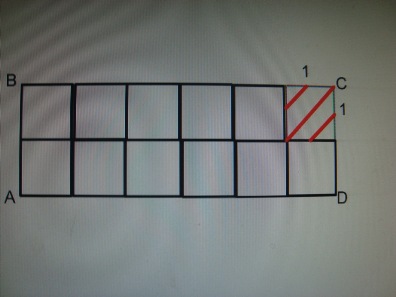
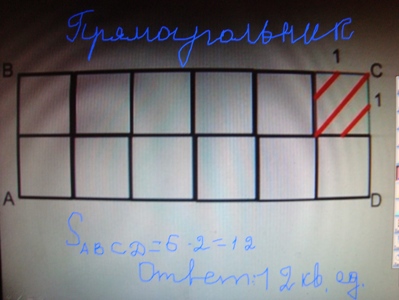
  !Прямоугольник
 
  !Прямоугольник
 
  |[[Изображение:Прямоугольник.JPG|Прямоугольник.JPG]]
 
  |[[Изображение:Прямоугольник.JPG|Прямоугольник.JPG]]
−
  |[[Изображение:|Изображение:]]
+
  |[[Изображение:Прямоуг_ученик.JPG|Прямоуг_ученик.JPG]]
 
  |-
 
  |-
 
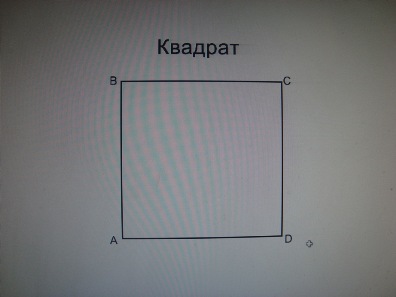
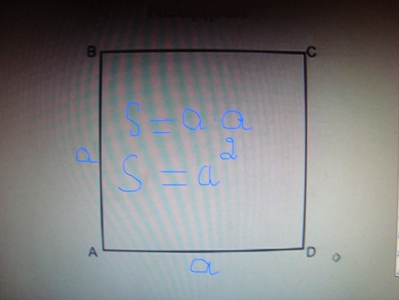
  !Квадрат
 
  !Квадрат
 
  |[[Изображение:Кадрат.JPG|right|]]
 
  |[[Изображение:Кадрат.JPG|right|]]
−
  |Ячейка 3*3
+
  |[[Изображение:Квадрат.JPG|Квадрат.JPG]]
 
  |-
 
  |-
 
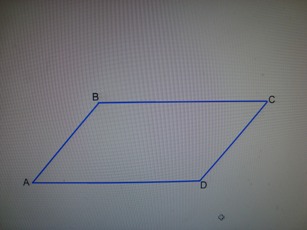
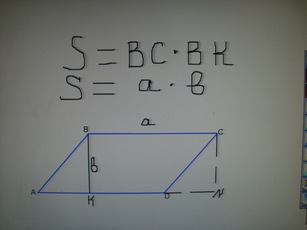
  !Параллелограмм
 
  !Параллелограмм
−
  |[[Изображение:|right|]]
+
  |[[Изображение:Парпар.JPG|Парпар.JPG]]
−
  |Ячейка 3*2
+
  |[[Изображение:Парпар22.JPG|Парпар22.JPG]]
 
  |-
 
  |-
 
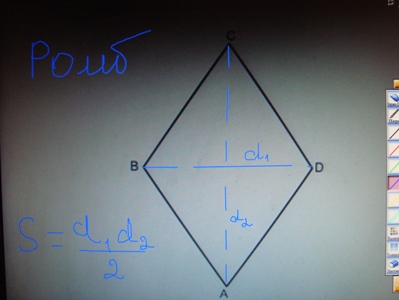
  !Ромб
 
  !Ромб
 
  |[[Изображение:Ромб.JPG|right|]]
 
  |[[Изображение:Ромб.JPG|right|]]
−
  |Ячейка 3*3
+
  |[[Изображение:Ромб22.JPG|right|]]           
 
  |-
 
  |-
 
  !Прямоугольный треугольник
 
  !Прямоугольный треугольник
 
  |[[Изображение:Прямоуг_треу.JPG|right|]]
 
  |[[Изображение:Прямоуг_треу.JPG|right|]]
−
  |[[Изображение:|Изображение:]]
+
  |[[Изображение:Прямтреуг.JPG|Прямтреуг.JPG]]            
 
  |-
 
  |-
 
  !Произвольный треугольник
 
  !Произвольный треугольник
Строка 125: Строка 150:
 
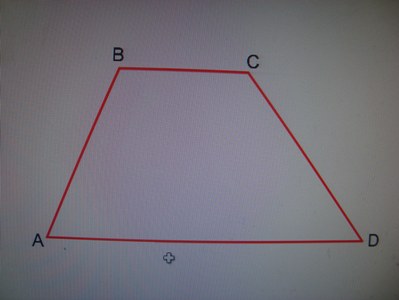
  !Трапеция
 
  !Трапеция
 
  |[[Изображение:Новая_трапеция_2.JPG|right|]]
 
  |[[Изображение:Новая_трапеция_2.JPG|right|]]
−
  |Ячейка 3*2
+
  |[[Изображение: Трапеция22.JPG|right|]]   
 
  |-
 
  |-
 
  !Правильный многоугольник
 
  !Правильный многоугольник
 
  |[[Изображение:Правильн_многоу.JPG|right|]]
 
  |[[Изображение:Правильн_многоу.JPG|right|]]
−
  |Ячейка 3*3
+
  |[[Изображение:Прав_мноугольJPG.JPG|right|]]                   
 
  |-
 
  |-
 
  !Окружность, вписанная в треугольник
 
  !Окружность, вписанная в треугольник
 
  |[[Изображение:Н=3.JPG|right|]]
 
  |[[Изображение:Н=3.JPG|right|]]
−
  |[[Изображение:|Изображение:]]
+
  |[[Изображение:Радиус_впис_окр.JPG|Радиус_впис_окр.JPG]]
 
  |-
 
  |-
 
  !Параллелограмм
 
  !Параллелограмм
 
  |[[Изображение:ДК=.JPG|right|]]
 
  |[[Изображение:ДК=.JPG|right|]]
−
  |Ячейка 3*3
+
  |[[Изображение:ПараллеДК=.JPG|right|]]             
 
  |-
 
  |-
 
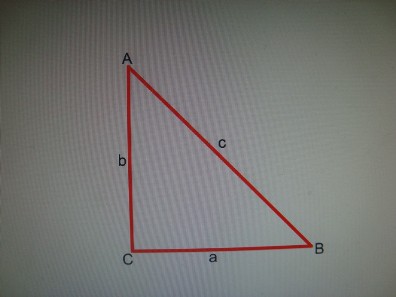
  !Треугольник
 
  !Треугольник
 
  |[[Изображение:По_теор_син.JPG|right|]]
 
  |[[Изображение:По_теор_син.JPG|right|]]
−
  |Ячейка 3*2
+
  |[[Изображение:По_теор_синусов.JPG|right|]]             
 
  |-
 
  |-
 
  !Пирамида(правильная n- угольная)
 
  !Пирамида(правильная n- угольная)
 
  |[[Изображение:ПирамидаJPG.JPG|right|]]
 
  |[[Изображение:ПирамидаJPG.JPG|right|]]
−
  |Ячейка 3*2
+
  |[[Изображение: Пир_прав_.JPG|right|]]       
 
  |-
 
  |-
 
  !Призма
 
  !Призма
 
  |[[Изображение:Призма2.JPG|right|]]
 
  |[[Изображение:Призма2.JPG|right|]]
−
  |Ячейка 3*3
+
  |[[Изображение:Призма.JPG|right|]]                   
 
  |-
 
  |-
 
  !Цилиндр
 
  !Цилиндр
 
  |[[Изображение:Цилиндр2.JPG|right|]]
 
  |[[Изображение:Цилиндр2.JPG|right|]]
−
  |[[Изображение:|Изображение:]]
+
  |[[Изображение:Цилиндр.JPG|Цилиндр.JPG]]
 
  |-
 
  |-
 
  !Шаровой пояс
 
  !Шаровой пояс
 
  |[[Изображение:Шаровой_пояс.JPG|right|]]
 
  |[[Изображение:Шаровой_пояс.JPG|right|]]
−
  |Ячейка 3*3
+
  |[[Изображение:Шар_сфера.JPG|right|]]                               
 
  |-
 
  |-
 
  !Конус
 
  !Конус
 
  |[[Изображение:Конус.JPG|right|]]
 
  |[[Изображение:Конус.JPG|right|]]
−
  |Ячейка 3*2
+
  |[[Изображение:Конус22.JPG |right|]]
 
  |-
 
  |-
 
  !Усеченный конус
 
  !Усеченный конус
 
  |[[Изображение:Усеч.конус.JPG|right|]]
 
  |[[Изображение:Усеч.конус.JPG|right|]]
−
  |Ячейка 3*3
+
  |[[Изображение:Усеч_конус.JPG|right|]]                           
 
  |-
 
  |-
 
  !Усеченная пирамида
 
  !Усеченная пирамида
 
  |[[Изображение:Усеч.пирамида.JPG|right|]]
 
  |[[Изображение:Усеч.пирамида.JPG|right|]]
−
  |Ячейка 3*3
+
  |[[Изображение:Усеч_пирам.JPG|right|]]                   
 
  |}
 
  |}
−
5. Закрепление.
+
4. Закрепление.
 +
 
 
1. Происхождение  коэффициента ½ в формулах площадей.
 
1. Происхождение  коэффициента ½ в формулах площадей.
−
2. Преобразование
+
 
−
3. Вычислить площадь ткани  для платья на выпускной бал( свои размеры проставить каждой ученице.
+
2. Преобразование S<sub>трап.</sub>  в  S<sub>ус.конуса</sub>
−
6. Домашнее задание:
+
−
              Мальчикам: расход обоев на свою гостиную;  
+
3. Вычислить площадь ткани  для платья на выпускной бал (свои размеры проставить каждой ученице).
−
              Девочкам:расход ткани на свое платье.
+
 
 +
5. Домашнее задание:
 +
 
 +
Мальчикам: расход обоев на свою гостиную;  
 +
 
 +
Девочкам:расход ткани на свое платье.
 +
 
 
Литература:
 
Литература:
 +
 +
1.Киселев А.П. геометрия,9-10.
 +
 +
2.Погорелов А.В. Геометрия, 7-11.
 +
 +
[[Категория:Проект ДООМ 2009-2010]]

Текущая версия на 06:06, 17 декабря 2009

Участник: Молдагалиева Дамира Ароновна,IDm063

Тема урока: Поверхности геометрических фигур

Класс:11

Цели:

1.Систематизация формул вычисления поверхностей всех геометрических фигур,изученных в школе.

2.тренировать способность: к анализу, сравнению, выявлению существенных свойств; развитие навыков и умений работы с программой Star Board.

3. воспитание информационной культуры учащихся, внимательности, аккуратности, дисциплинированности; умения работать в группах.

Подготовка к уроку:

1)интерактивная доска

2)проектор

3)notebook с программным обеспечением Star Board.

4)компьютерный класс.

18).Запись на слайде: Природа говорит языком математики, буквы этого языка-круги, треугольники и иные математические фигуры. Галилей.


Ход урока:

1. Организационный момент.

Проверка учительской презентации в каждом компьютере для работ учащихся в режиме интерактивной доски Star Board.

2.Устная работа.

а)Назвать единицы измерения поверхностей.

б)Назвать соотношения между ними.

в)Оценить площадь стола, площадь классной доски, площадь потолка в классе, площадь дверного проема, площадь окна, тетрадного листа.

г) Назвать какую нибудь деятельность человека ,связанную с учетом площади(артист-площадь сцены, летчик- площадь посадочной полосы, повар- площадь плиты, швея-площадь материи, писатель-площадь страниц и т.д.).

Учитель: Вы оканчиваете школу, уходите в жизнь. Дороги разные, но везде надо будет применять полученные в школе знания.

3.Целью сегодняшнего урока является систематизация формул вычисления поверхностей всех геометрических фигур, изученных нами. Оказывается, достаточно отчетливо помнить одну основную формулу-формулу площади прямоугольника, чтобы вычислить площадь любой поверхности.

Учащиеся парами садятся за компьютер, где открывают программу POWER point c презентацией по теме, и задачи в чертежах сопровождают решениями. После выполнения всех заданий учащиеся имеют возможность продемонстрировать свои презентации в режиме интерактивной доски.Здесь же учащиеся, сидящие за персональными компьютерами имеют возможность, при наличии ошибок, сразу же исправить их.


Прямоугольник.Два ряда квадратных единиц по 6 в ряду: Площадь АВСД S=ab (1)

Квадрат По формуле (1) S=a2;

Параллелограмм. Отрезаем АВК и ставим его вместо DCN. Получаем прямоугольник ВСNК .По формуле (1) имеем: S=ВС * ВК= ab.

Ромб. Опять используем формулу (1). Площадь ромба равна половине площади прямоугольника. По формуле (1) имеем S= d1d2/2где d1,d2- диагонали

Прямоугольный треугольник. По формуле(1) S=1/2 ab

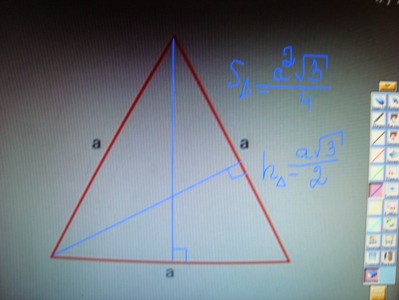
Произвольный треугольник. S=1/2Sпараллелограмма, Sтреуг.=1/2 ah.

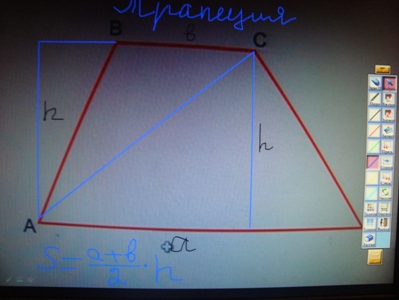
Трапеция. Сумма двух треугольников с общей высотой. Sтрап=1/2 (AD+BC)*h.

Sтрап=1/2 ( a+b)*h.

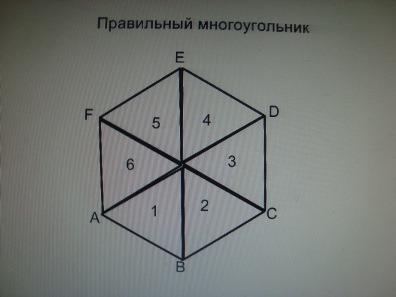
Правильный многоугольник.

SABCDEF =1/2 PABCDEF * r, где r- радиус вписанной окружности.

Вписанная окружность.При n=3 имеем случай, т.е. вычисляем SABC=1/2РABC * ОК, SABC=P * r.

Параллелограмм.DК=в sin a, SABCD= a b sin a, SADК= 1/2 a b sin a.


Треугольник.SAВС= 1/2 a b sin С,

По теореме синусов имеем: a /sin A = b/ sin В, b= a sin В/ sin A, SAВС=1/2 a2 sin В sin С/ sin A.

Пирамида (правильная n-угольная).

S бок. пир=1/2 АВ * SК*n=1/2 АВ * n*SК=1/2РАВСD*SК, где SК-апофема.

Призма (параллелепипед)

S бок=РАВСDЕ*АА1.

Цилиндр.

Развертка боковой поверхности-прямоугольник АВСD. По формуле (1) имеем:

Sбок.цил=СН; Sбок.цил=2пRН

Шаровой пояс.

В математике часто используем предельные переходы. Если радиус кривизны сферы стремится к бесконечности, а высота шарового слоя стремится к нулю, то шаровой слой принимается за цилиндр, оставаясь все- таки шаровым слоем. Высота слоя H.H=2R. Секущие плоскости ОК=h можно расположить так, что образуется шаровой сегмент или целый шар.Sшар.сег=2пRh, где R-радиус большого круга сферы, h-высота сегмента.S<сферы</sub>=2пR*2R=4пR2 H=2R.Секущие плоскости ОК=h можно расположить так, что образуется шаровой сегмент или целый шар. S =2пRh, где R-радиус большого круга сферы, h-высота сегмента. S=2пR2R=4пR2.

Конус.

Sбок.кон=limSбок.пир=1/2Cl=1/2пRl.

Усеченный конус.

Sбок.ус.кон=limSбок.ус.пир, Sбок.ус.кон=1/2(2пr+2пR)*l=п(R+r)*l.

Усеченная пирамида.

Sтрап.=1/2(а+b)*h,

Sбок= 1/2(аn+bn)*h,

Sбок=1/2(Рв+Рн)*mМ.


Название фигуры Деятельность учителя Деятельность ученика
Прямоугольник Прямоугольник.JPG Прямоуг_ученик.JPG
Квадрат
Кадрат.JPG
 Квадрат.JPG
Параллелограмм Парпар.JPG Парпар22.JPG
Ромб
Ромб.JPG
Ромб22.JPG
Прямоугольный треугольник
Прямоуг треу.JPG
 Прямтреуг.JPG
Произвольный треугольник
Треугль кос учитель.JPG
Треугль кос ученик.JPG
Правильный треугольник
Прав треуго.учит.JPG
Прав треугльнученик.JPG
Трапеция
Новая трапеция 2.JPG
Трапеция22.JPG
Правильный многоугольник
Правильн многоу.JPG
Прав мноугольJPG.JPG
Окружность, вписанная в треугольник
Н=3.JPG
 Радиус_впис_окр.JPG
Параллелограмм
ДК=.JPG
ПараллеДК=.JPG
Треугольник
По теор син.JPG
По теор синусов.JPG
Пирамида(правильная n- угольная)
ПирамидаJPG.JPG
Пир прав .JPG
Призма
Призма2.JPG
Призма.JPG
Цилиндр
Цилиндр2.JPG
 Цилиндр.JPG
Шаровой пояс
Шаровой пояс.JPG
Шар сфера.JPG
Конус
Конус.JPG
Конус22.JPG
Усеченный конус
Усеч.конус.JPG
Усеч конус.JPG
Усеченная пирамида
Усеч.пирамида.JPG
Усеч пирам.JPG

4. Закрепление.

1. Происхождение коэффициента ½ в формулах площадей.

2. Преобразование Sтрап. в Sус.конуса

3. Вычислить площадь ткани для платья на выпускной бал (свои размеры проставить каждой ученице).

5. Домашнее задание:

Мальчикам: расход обоев на свою гостиную;

Девочкам:расход ткани на свое платье.

Литература:

1.Киселев А.П. геометрия,9-10.

2.Погорелов А.В. Геометрия, 7-11.

Источник — «http://wiki.tgl.net.ru/index.php?title=%D0%A1%D0%B5%D0%BC%D0%B8%D0%BD%D0%B0%D1%80_%D0%94%D0%9E%D0%9E%D0%9C_%D0%9F%D0%BE%D0%B2%D0%B5%D1%80%D1%85%D0%BD%D0%BE%D1%81%D1%82%D0%B8_%D0%B3%D0%B5%D0%BE%D0%BC%D0%B5%D1%82%D1%80%D0%B8%D1%87%D0%B5%D1%81%D0%BA%D0%B8%D1%85_%D1%84%D0%B8%D0%B3%D1%83%D1%80&oldid=109003»
наши друзья
http://аудиохрестоматия.рф/