Семинар ДООМ "Решение треугольников"
(→'''Тема «Решение треугольников»'''Класс 9) |
(→Методическая разработка урока геометрии.) |
||
| (не показаны 7 промежуточных версий 1 участника) | |||
| Строка 1: | Строка 1: | ||
== Методическая разработка урока геометрии. == | == Методическая разработка урока геометрии. == | ||
| − | Учитель [[Участник: Иейник Наталия Дмитриевна|Иейник Наталия Дмитриевна]] | + | Учитель [[Участник: Иейник Наталия Дмитриевна|Иейник Наталия Дмитриевна]] --[[Участник:Многогранники IDm071|Многогранники IDm071]] ) |
== '''Тема «Решение треугольников»'''Класс 9 == | == '''Тема «Решение треугольников»'''Класс 9 == | ||
| Строка 6: | Строка 6: | ||
'''Способ работы:''' фронтальный.<br> | '''Способ работы:''' фронтальный.<br> | ||
'''Педагогическая технология:''' технология модульного обучения.<br> | '''Педагогическая технология:''' технология модульного обучения.<br> | ||
| − | '''Оборудование:''' Учебник Погорелов А.В. Геометрия 7-9, таблицы Брадиса, проектор, | + | '''Оборудование:''' Учебник Погорелов А.В. Геометрия 7-9, таблицы Брадиса, проектор, [[Медиа:Решение_треугольников.ppt| Презентация «Решение треугольников».]]<br> |
'''Цель:''' Ввести понятие «Решения треугольника» и познакомить учащихся с типологией задач по теме и методами их решения.<br> | '''Цель:''' Ввести понятие «Решения треугольника» и познакомить учащихся с типологией задач по теме и методами их решения.<br> | ||
| Строка 21: | Строка 21: | ||
Демонстрируется слайд 2.<br> | Демонстрируется слайд 2.<br> | ||
| − | [[Изображение:cevv.jpg]] | + | [[Изображение:cevv.jpg|400px]] |
<br> | <br> | ||
Вспомним теорему косинусов? (квадрат стороны треугольника равен сумме квадратов двух других сторон без их удвоенного произведения на косинус угла между ними).<br> | Вспомним теорему косинусов? (квадрат стороны треугольника равен сумме квадратов двух других сторон без их удвоенного произведения на косинус угла между ними).<br> | ||
| − | [[Изображение:cevv2.jpg]]<br> | + | [[Изображение:cevv2.jpg|400px]]<br> |
И ее частный случай, теорему Пифагора (Квадрат гипонетузы равен сумме квадратов катетов).<br> | И ее частный случай, теорему Пифагора (Квадрат гипонетузы равен сумме квадратов катетов).<br> | ||
И наконец, теорема синусов? (стороны треугольника пропорциональны синусам противолежащих углов).<br> | И наконец, теорема синусов? (стороны треугольника пропорциональны синусам противолежащих углов).<br> | ||
| − | [[Изображение:cevv1.jpg]] | + | [[Изображение:cevv1.jpg|400px]] |
'''''3. Изучение нового материала.'''''<br> | '''''3. Изучение нового материала.'''''<br> | ||
| − | Итак. Какие 3 элемента у треугольника могут быть известны? (три стороны, две стороны и угол между ними, две стороны и угол лежащий напротив одной из них, одна сторона и два угла)<br> | + | Итак. Какие 3 элемента у треугольника могут быть известны? (три стороны, две стороны и угол между ними, две стороны и угол лежащий напротив одной из них, одна сторона и два угла) <br> |
| − | ''1. Три стороны:'' | + | ''1. Три стороны:''<br> |
| + | [[Изображение:сумм3.jpg|400px]]<br> | ||
| + | Учитель поэтапно объясняет ход решения, учащиеся записывают. | ||
| + | |||
| + | |||
| + | 2. По двум сторонам и углу между ними: | ||
| + | |||
| + | [[Изображение:сумм4.jpg|400px]] | ||
| + | |||
| + | |||
| + | Учитель поэтапно объясняет ход решения, учащиеся записывают. | ||
| + | |||
| + | |||
| + | 3. По двум сторонам и углу противолежащему одной из них: | ||
| + | |||
| + | |||
| + | [[Изображение:сумм5.jpg|400px]] | ||
| + | |||
| + | |||
| + | Ребята, обратите внимание, что у данного типа задач может быть два решения, главное не забудьте потом проверить, что напротив большей стороны получился больший угол. | ||
| + | |||
| + | |||
| + | 4. По стороне и двум углам. | ||
| + | |||
| + | |||
| + | [[Изображение:сумм6.jpg|400px]] | ||
| + | |||
| + | |||
| + | |||
| + | Даже если известен не прилежащий угол, то ход решения будет таким же. | ||
| + | |||
| + | |||
| + | [[Изображение:сумм7.jpg|400px]] | ||
| + | |||
| + | |||
| + | '''''4. Первичное закрепление изученного.''''' <br> | ||
| + | А теперь для закрепления решим задачу. <br> | ||
| + | Дано: a = 5; β = 300 <br> | ||
| + | γ = 450<br> | ||
| + | Найти b, с, α. | ||
| + | <br> | ||
| + | Один учащийся решает на доске, все остальные – в тетради, затем демонстрируется слайд с правильным решением:<br> | ||
| + | [[Изображение:сумм8.jpg|400px]]<br> | ||
| + | |||
| + | '''''5. Итог урока. Постановка домашнего задания.'''''Итак в заключении ответьте на мои вопросы:<br> | ||
| + | 1. Что значит решить треугольник?<br> | ||
| + | 2. Сколько типов задач на решение треугольника существует?<br> | ||
| + | 3. Когда может получиться 2 решения?<br> | ||
| + | 4. По каким трем элементам нельзя решить треугольник и почему?<br> | ||
| + | |||
| + | Для закрепления материала выполните домашнее задание:<br> | ||
| + | Повторить: теоремы Пифагора, синусов, косинусов, сумма углов треугольника.<br> | ||
| + | Решать задачи № 27 (a) 28 (a) 29 (a) <br> | ||
| + | Творческое задание. Придумать другой ход решения каждой задачи и оформить в виде компьютерной презкнтации.<br> | ||
| + | |||
| + | [[Категория:Проект ДООМ 2009-2010]] | ||
Текущая версия на 00:07, 20 декабря 2009
Методическая разработка урока геометрии.
Учитель Иейник Наталия Дмитриевна --Многогранники IDm071 )
Тема «Решение треугольников»Класс 9
Тип урока: Урок изучения нового материала.
Способ работы: фронтальный.
Педагогическая технология: технология модульного обучения.
Оборудование: Учебник Погорелов А.В. Геометрия 7-9, таблицы Брадиса, проектор, Презентация «Решение треугольников».
Цель: Ввести понятие «Решения треугольника» и познакомить учащихся с типологией задач по теме и методами их решения.
Ход урока.
1. Введение.
Здравствуйте ребята. Сегодня на уроке мы с вами научимся «Решать треугольник». Решить треугольник – это значит, по некоторым его данным сторонам и углам найти остальные стороны и углы.
2. Активизация знаний.
Итак, сколько всего элементов у треугольника? (шесть: 3 стороны и три угла)
Решить треугольник можно, если известно какие-нибудь три его элемента, исключая случай, когда известны 3 угла и не одной стороны. Кстати, почему? (у подобных треугольников углы равны, поэтому однозначно найти стороны нельзя).
Для того, чтобы решить треугольник нам необходимо вспомнить некоторые правила и теоремы, связанные с ним.
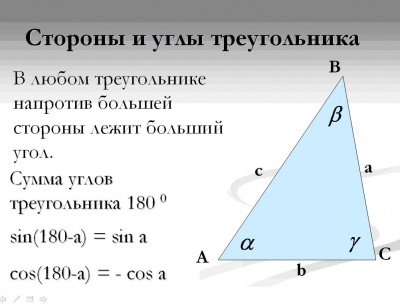
Повторим, как соотносятся стороны и угла треугольника в зависимости от величины? (напротив большей стороны лежит больший угол).
Чему равна сумма углов треугольника? (180 градусов)
Демонстрируется слайд 2.
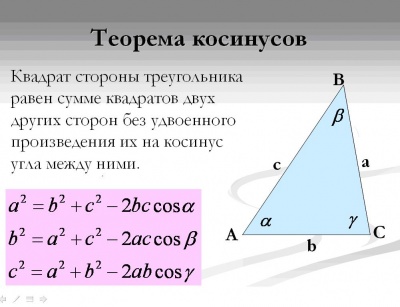
Вспомним теорему косинусов? (квадрат стороны треугольника равен сумме квадратов двух других сторон без их удвоенного произведения на косинус угла между ними).
И ее частный случай, теорему Пифагора (Квадрат гипонетузы равен сумме квадратов катетов).
И наконец, теорема синусов? (стороны треугольника пропорциональны синусам противолежащих углов).
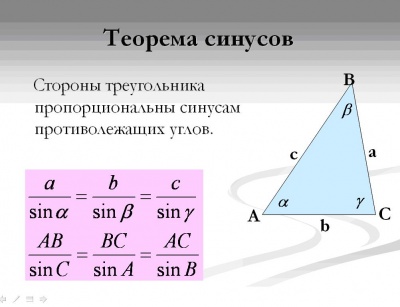
3. Изучение нового материала.
Итак. Какие 3 элемента у треугольника могут быть известны? (три стороны, две стороны и угол между ними, две стороны и угол лежащий напротив одной из них, одна сторона и два угла)
1. Три стороны:
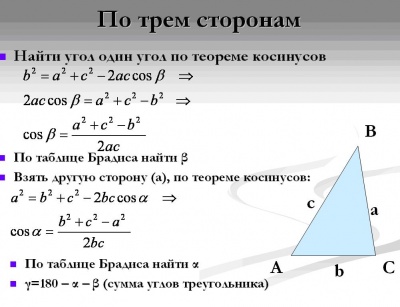
Учитель поэтапно объясняет ход решения, учащиеся записывают.
2. По двум сторонам и углу между ними:
Учитель поэтапно объясняет ход решения, учащиеся записывают.
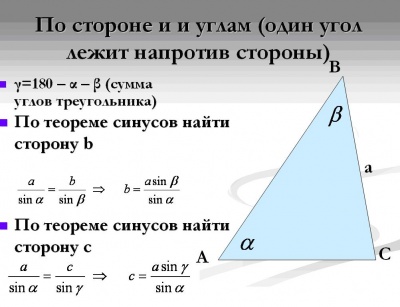
3. По двум сторонам и углу противолежащему одной из них:
Ребята, обратите внимание, что у данного типа задач может быть два решения, главное не забудьте потом проверить, что напротив большей стороны получился больший угол.
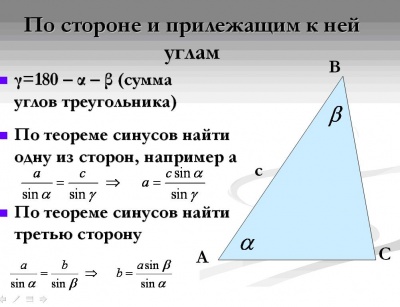
4. По стороне и двум углам.
Даже если известен не прилежащий угол, то ход решения будет таким же.
4. Первичное закрепление изученного.
А теперь для закрепления решим задачу.
Дано: a = 5; β = 300
γ = 450
Найти b, с, α.
Один учащийся решает на доске, все остальные – в тетради, затем демонстрируется слайд с правильным решением:

5. Итог урока. Постановка домашнего задания.Итак в заключении ответьте на мои вопросы:
1. Что значит решить треугольник?
2. Сколько типов задач на решение треугольника существует?
3. Когда может получиться 2 решения?
4. По каким трем элементам нельзя решить треугольник и почему?
Для закрепления материала выполните домашнее задание:
Повторить: теоремы Пифагора, синусов, косинусов, сумма углов треугольника.
Решать задачи № 27 (a) 28 (a) 29 (a)
Творческое задание. Придумать другой ход решения каждой задачи и оформить в виде компьютерной презкнтации.