Обсуждение:Семинар ДООМ. Решение комбинаторных задач с помощью графов
| (не показаны 8 промежуточных версий 5 участников) | |||
| Строка 10: | Строка 10: | ||
Алфавит племени Пиджен состоит из 4-ёх букв. Аборигены закодировали слово СDAB с использованием следующей таблицы: | Алфавит племени Пиджен состоит из 4-ёх букв. Аборигены закодировали слово СDAB с использованием следующей таблицы: | ||
| + | |||
[[Изображение:Smt1.JPG]] | [[Изображение:Smt1.JPG]] | ||
| + | |||
| + | и передали его не сделав промежутков, отделяющих одну букву от другой. Количество способов прочтения переданного сообщения равно? | ||
| + | |||
| + | '''Задача2.''' | ||
| + | |||
| + | Алфавит племени Пиджен состоит из 4-ёх букв. Аборигены закодировали слово DСAD с использованием следующей таблицы: | ||
| + | |||
| + | [[Изображение:Smt2.JPG]] | ||
| + | |||
| + | и передали его не сделав промежутков, отделяющих одну букву от другой. Количество способов прочтения переданного сообщения равно? | ||
| + | |||
| + | '''Задача3.''' | ||
| + | |||
| + | Алфавит племени Пиджен состоит из 4-ёх букв. Аборигены закодировали слово ВААС с использованием следующей таблицы: | ||
| + | |||
| + | [[Изображение:Smt3.JPG]] | ||
| + | |||
| + | и передали его не сделав промежутков, отделяющих одну букву от другой. Количество способов прочтения переданного сообщения равно? | ||
| + | |||
| + | '''Задача4.''' | ||
| + | |||
| + | Алфавит племени Пиджен состоит из 4-ёх букв. Аборигены закодировали слово DBAD с использованием следующей таблицы: | ||
| + | |||
| + | [[Изображение:Smt4.JPG]] | ||
| + | |||
| + | и передали его не сделав промежутков, отделяющих одну букву от другой. Количество способов прочтения переданного сообщения равно? | ||
| + | |||
| + | '''РЕШЕНИЕ ЗАДАЧИ №1''' | ||
| + | |||
| + | Алгоритм: | ||
| + | |||
| + | 1. С помощью таблицы кодируем сообщение СDAB, получаем код 100101 | ||
| + | |||
| + | 2. Записываем код в вершину будущего графа | ||
| + | |||
| + | 3. Анализируем: какая буква может стоять на первом месте? Есть два варианта. В или С. Значит, из нашей вершины будет выходить два ребра, в вершины, которыми они заканчиваются, пишем еще не расшифрованный код(т.е В кодируется 1, значит код 100101 мы трактуем как В00101, пишем 00101, С кодируется как 10, получаем С0101, пишем 0101) | ||
| + | |||
| + | 4. Повторяем п.3 для всех вершин, пока не останется одна буква. | ||
| + | |||
| + | 5. Количество листьев графа определяет количество вариантов декодирования (в нашем случае 10). Варианты декодирования также просматриваются. | ||
| + | |||
| + | [[Изображение:Svg.JPG]] | ||
| + | |||
| + | Дальнейших Вам успехов, Ирина Владимировна! | ||
| + | |||
| + | --[[Участник:Иванова Елена|Иванова Елена]] 10:08, 15 ноября 2007 (UZT) | ||
| + | |||
| + | Здравствуйте! | ||
| + | |||
| + | Очень хорошо, что дети знакомятся с теорией графов с 5 класса. Интересно представлена внеурочная работа с учащимися. Применяются задачи на развитие логического мышления, вызывающие интерес к предмету. | ||
| + | |||
| + | Успехов вам в работе! | ||
| + | --[[Участник:Хазова Людмила Модестовна|Хазова Людмила Модестовна]] 17:13, 21 ноября 2007 (UZT) | ||
| + | |||
| + | Здравствуйте, Ирина Владимировна | ||
| + | Очень понравилась Ваша статья, задач много и они доступны многим школьникам. | ||
| + | Хотелось бы поделиться решением задачи 4.1, которое позволяет использовать не такой громоздкий граф и воспользоваться правилом умножения. | ||
| + | |||
| + | Всего из цифр 1,2,3 можно составить 3*3*3 трехзначных числа. Посчитаем число чисел, в которых за 2 стоит 3. если 23 стоят в начале числа, последнюю цифру можно выбрать 3 способами (уместен граф) - таких чисел 3, аналогично 3 числа, где пара 23 стоит в конце числа. Тогда чисел, где нет пары 23, 3*3*3-3-3=21. | ||
| + | '''''[[Участник:Коннова Елена|Коннова Елена]] 23:50, 27 ноября 2007 (UZT)''''' | ||
| + | |||
| + | Здравстуйте, Ирина Владимировна! Занятие Ваше мне сразу понравилось. Некоторые ваши задачи мы с ребятами использовали для объяснения темы "Графы" в 5,6 классах. Они воспринимаются детьми очень легко, с интересом. Большое Вам спасибо! | ||
| + | --[[Участник:Тимофеева Надежда Николаевна|Тимофеева Надежда Николаевна]] 23:16, 6 декабря 2007 (UZT) | ||
| + | |||
| + | Введение элементов теории вероятности в школьную программу добавило много проблем.Одна из них, каким образом доступно объяснить школьникам 5-6 классов понятия комбинаторики. Ваше занятие это демонстрирует очень успешно. | ||
| + | Команда 061 | ||
| + | --[[Участник:Москевич Лариса Вячеславовна|Москевич Лариса Вячеславовна]] 23:38, 7 декабря 2007 (UZT) | ||
Текущая версия на 00:26, 8 декабря 2007
Здравствуйте, Ирина Владимировна!
Мне очень понравилось, что занятие Вашего кружка посвящено решению конкретного класса задач на применение графов, что задачи разбиты на блоки и внутри каждого блока приводится несколько вариантов заданий. Очень четко просматривается логика в изложении материала, его структура. Мне кажется, что именно такой подход формирует устойчивые навыки в решении задач, способствует полному усвоению знаний.
Не знаю, будет ли это уместным, но мне хочется предложить Вам еще один вид задач, которые, как мне кажется, созвучны теме Вашего занятия, может быть Вам это пригодиться. Это задачи, которые предлагались учащимся на централизованном тестировании по информатике. К сожалению, авторы тестов и после тестирования не публикуют оптимальных способов решения задач, информатики нашей школы при подготовке к ЦТ предлагают решать задачи такого типа с помощью графов.
Итак, задачи:
Задача1.
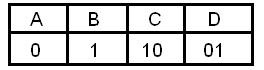
Алфавит племени Пиджен состоит из 4-ёх букв. Аборигены закодировали слово СDAB с использованием следующей таблицы:
и передали его не сделав промежутков, отделяющих одну букву от другой. Количество способов прочтения переданного сообщения равно?
Задача2.
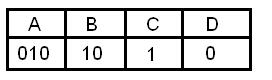
Алфавит племени Пиджен состоит из 4-ёх букв. Аборигены закодировали слово DСAD с использованием следующей таблицы:
и передали его не сделав промежутков, отделяющих одну букву от другой. Количество способов прочтения переданного сообщения равно?
Задача3.
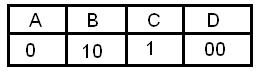
Алфавит племени Пиджен состоит из 4-ёх букв. Аборигены закодировали слово ВААС с использованием следующей таблицы:
и передали его не сделав промежутков, отделяющих одну букву от другой. Количество способов прочтения переданного сообщения равно?
Задача4.
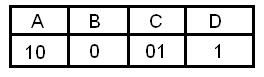
Алфавит племени Пиджен состоит из 4-ёх букв. Аборигены закодировали слово DBAD с использованием следующей таблицы:
и передали его не сделав промежутков, отделяющих одну букву от другой. Количество способов прочтения переданного сообщения равно?
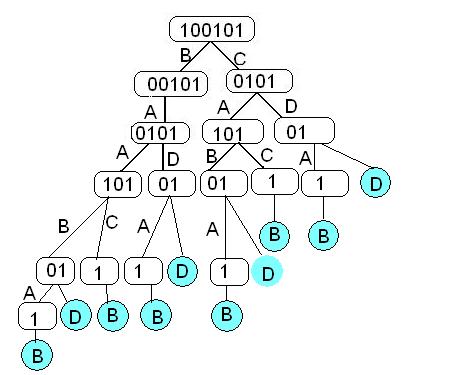
РЕШЕНИЕ ЗАДАЧИ №1
Алгоритм:
1. С помощью таблицы кодируем сообщение СDAB, получаем код 100101
2. Записываем код в вершину будущего графа
3. Анализируем: какая буква может стоять на первом месте? Есть два варианта. В или С. Значит, из нашей вершины будет выходить два ребра, в вершины, которыми они заканчиваются, пишем еще не расшифрованный код(т.е В кодируется 1, значит код 100101 мы трактуем как В00101, пишем 00101, С кодируется как 10, получаем С0101, пишем 0101)
4. Повторяем п.3 для всех вершин, пока не останется одна буква.
5. Количество листьев графа определяет количество вариантов декодирования (в нашем случае 10). Варианты декодирования также просматриваются.
Дальнейших Вам успехов, Ирина Владимировна!
--Иванова Елена 10:08, 15 ноября 2007 (UZT)
Здравствуйте!
Очень хорошо, что дети знакомятся с теорией графов с 5 класса. Интересно представлена внеурочная работа с учащимися. Применяются задачи на развитие логического мышления, вызывающие интерес к предмету.
Успехов вам в работе! --Хазова Людмила Модестовна 17:13, 21 ноября 2007 (UZT)
Здравствуйте, Ирина Владимировна Очень понравилась Ваша статья, задач много и они доступны многим школьникам. Хотелось бы поделиться решением задачи 4.1, которое позволяет использовать не такой громоздкий граф и воспользоваться правилом умножения.
Всего из цифр 1,2,3 можно составить 3*3*3 трехзначных числа. Посчитаем число чисел, в которых за 2 стоит 3. если 23 стоят в начале числа, последнюю цифру можно выбрать 3 способами (уместен граф) - таких чисел 3, аналогично 3 числа, где пара 23 стоит в конце числа. Тогда чисел, где нет пары 23, 3*3*3-3-3=21. Коннова Елена 23:50, 27 ноября 2007 (UZT)
Здравстуйте, Ирина Владимировна! Занятие Ваше мне сразу понравилось. Некоторые ваши задачи мы с ребятами использовали для объяснения темы "Графы" в 5,6 классах. Они воспринимаются детьми очень легко, с интересом. Большое Вам спасибо! --Тимофеева Надежда Николаевна 23:16, 6 декабря 2007 (UZT)
Введение элементов теории вероятности в школьную программу добавило много проблем.Одна из них, каким образом доступно объяснить школьникам 5-6 классов понятия комбинаторики. Ваше занятие это демонстрирует очень успешно. Команда 061 --Москевич Лариса Вячеславовна 23:38, 7 декабря 2007 (UZT)