Семинар ДООМ "Применение графов к решению логических задач."
(Новая: Основой применения графов для решения логических задач служит выявление и последовательное исключ...) |
|||
| (не показаны 7 промежуточных версий 1 участника) | |||
| Строка 1: | Строка 1: | ||
| + | [[участник: Болонина Людмила Александровна, 022.]] | ||
| + | ''Краткое изложение факультативного занятия на тему:'' | ||
| + | '''«Применение графов к решению логических задач»''' | ||
| + | |||
| + | '''Цель:''' разобрать закономерности решения логических задач с помощью графов. | ||
| + | |||
| + | '''Ход занятия:''' | ||
| + | |||
| + | '''1)''' Объяснение учителем. | ||
| + | |||
| + | '''2)''' Решение логических задач с помощью графов. | ||
| + | |||
| + | '''3)''' Подведение итогов. | ||
| + | |||
| + | '''4)''' Домашнее задание. | ||
Основой применения графов для решения логических задач служит выявление и последовательное исключение логических возможностей, задаваемых условиями задач. Это выявление и исключение логических возможностей часто может быть истолковано с помощью построения и рассмотрения соответствующих графов. | Основой применения графов для решения логических задач служит выявление и последовательное исключение логических возможностей, задаваемых условиями задач. Это выявление и исключение логических возможностей часто может быть истолковано с помощью построения и рассмотрения соответствующих графов. | ||
| − | Задача 1. | + | |
| + | '''Задача 1.''' | ||
| + | |||
Из трех человек, стоящих рядом, один всегда говорит правду (правдивый), другой всегда лжет (лжец), а третий, смотря по обстоятельствам, говорит правду или ложь («дипломат»). У стоящего слева спросили: «Кто стоит рядом с тобой?» Он ответил: «Правдолюб». Стоящему в центре, задали вопрос: «Кто ты?», и он ответил: «Я дипломат». Когда у стоящего справа спросили: «Кто стоит рядом с тобой?», он ответил: «Лжец». Кто где стоял? | Из трех человек, стоящих рядом, один всегда говорит правду (правдивый), другой всегда лжет (лжец), а третий, смотря по обстоятельствам, говорит правду или ложь («дипломат»). У стоящего слева спросили: «Кто стоит рядом с тобой?» Он ответил: «Правдолюб». Стоящему в центре, задали вопрос: «Кто ты?», и он ответил: «Я дипломат». Когда у стоящего справа спросили: «Кто стоит рядом с тобой?», он ответил: «Лжец». Кто где стоял? | ||
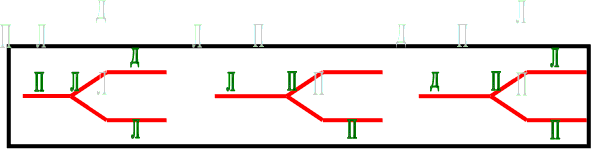
Если в данной задаче ребро графа будет соответствовать месту, занимаемому тем или иным человеком, то нам могут представиться следующие возможности. | Если в данной задаче ребро графа будет соответствовать месту, занимаемому тем или иным человеком, то нам могут представиться следующие возможности. | ||
| + | |||
| + | [[Изображение:r111.gif]] | ||
| + | '''Решение:''' | ||
Рассмотрим первую возможность. Если «правдолюб» стоит слева, то рядом с ним, судя по его ответу, находится «правдолюб». У нас же стоит лжец. Рассмотрев таким образом все остальные возможности, мы придем к выводу, что расстановка «дипломат», «лжец», «правдолюб» удовлетворяет задаче. Действительно, если «правдолюб» стоит справа, то, по его ответу, рядом с ним «лжец», что выполняется. Стоящий в центре заявляет, что он «дипломат», и следовательно, лжет, а стоящий справа также лжет. Таким образом все условия задачи выполнены. В качестве задачи второго типа можно предложить следующую. | Рассмотрим первую возможность. Если «правдолюб» стоит слева, то рядом с ним, судя по его ответу, находится «правдолюб». У нас же стоит лжец. Рассмотрев таким образом все остальные возможности, мы придем к выводу, что расстановка «дипломат», «лжец», «правдолюб» удовлетворяет задаче. Действительно, если «правдолюб» стоит справа, то, по его ответу, рядом с ним «лжец», что выполняется. Стоящий в центре заявляет, что он «дипломат», и следовательно, лжет, а стоящий справа также лжет. Таким образом все условия задачи выполнены. В качестве задачи второго типа можно предложить следующую. | ||
| − | Задача 2. | + | |
| + | '''Задача 2.''' | ||
| + | |||
В пяти корзинах лежали яблоки пяти разных сортов. Яблоки первого сорта лежат в корзинах Г и Д; яблоки второго сорта - в корзинах А. Б, Г; в корзинах А, Б, В имеются яблоки пятого сорта, в корзине В имеются к тому же яблоки четвертого сорта, а в корзине Д-третьего. Пронумеруйте каждую корзину так, чтобы в корзине №1 были яблоки первого сорта (хотя бы одно); в корзине № 2-второго и т.д. | В пяти корзинах лежали яблоки пяти разных сортов. Яблоки первого сорта лежат в корзинах Г и Д; яблоки второго сорта - в корзинах А. Б, Г; в корзинах А, Б, В имеются яблоки пятого сорта, в корзине В имеются к тому же яблоки четвертого сорта, а в корзине Д-третьего. Пронумеруйте каждую корзину так, чтобы в корзине №1 были яблоки первого сорта (хотя бы одно); в корзине № 2-второго и т.д. | ||
| − | Решение: Составим граф: | + | |
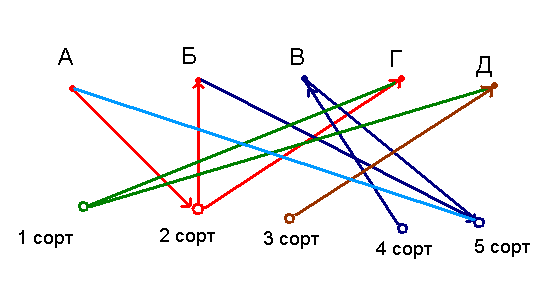
| + | '''Решение:''' Составим граф: | ||
| + | [[Изображение:r222.gif]] | ||
| − | + | ''' Ответ:''' №1-Г; №2-А или №2-Б; №3-Д; №4-В; №5-Б или №5-А | |
| − | + | ||
Возникает вопрос: так ли уж нужны были графы в этой задаче? Разве нельзя прийти к решению логическим путем? Можно, но графы придали условия наглядность, упростили решение. | Возникает вопрос: так ли уж нужны были графы в этой задаче? Разве нельзя прийти к решению логическим путем? Можно, но графы придали условия наглядность, упростили решение. | ||
| − | |||
| − | |||
| + | '''Задача 3.''' | ||
| + | |||
| + | В обеденный перерыв предприниматели разговорились, кто сколько газет читает. Выяснилось, что каждый выписывает и читает две и только две газеты, каждую газету читают пять человек, и любая комбинация читается одним человеком. Сколько названий газет выписывают предприниматели? Сколько всего было человек? | ||
| − | + | '''Решение:''' | |
| + | |||
| + | |||
| + | [[Изображение:r333.gif]] | ||
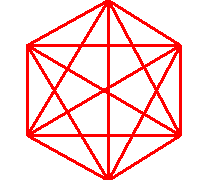
Решение этой задачи достигается построением следующего графа, где каждая вершина обозначает соответствующую газету и соответственно 5 подписчиков, а каждое ребро будет соответствовать одному подписчику. | Решение этой задачи достигается построением следующего графа, где каждая вершина обозначает соответствующую газету и соответственно 5 подписчиков, а каждое ребро будет соответствовать одному подписчику. | ||
| Строка 28: | Строка 55: | ||
6*(6-1)/2=15 чел. | 6*(6-1)/2=15 чел. | ||
Полезно решать логические задачи разными методами. Например, следующую задачу можно решить способом логических квадратов и с помощью графов. | Полезно решать логические задачи разными методами. Например, следующую задачу можно решить способом логических квадратов и с помощью графов. | ||
| − | Задача 3. | + | |
| + | '''Задача 3.''' | ||
| + | |||
Три ученицы - Аня, Валя. Катя - участвовали в новогоднем бале - маскараде. Одна из них была в красном костюме, другая - в белом, третья - в синем. Если сказать, что Аня была в красном, Валя – не в красном, и Катя –не в синем, то одно из этих утверждений будет верным, а два других –неверными. В каком костюме была каждая из учениц? | Три ученицы - Аня, Валя. Катя - участвовали в новогоднем бале - маскараде. Одна из них была в красном костюме, другая - в белом, третья - в синем. Если сказать, что Аня была в красном, Валя – не в красном, и Катя –не в синем, то одно из этих утверждений будет верным, а два других –неверными. В каком костюме была каждая из учениц? | ||
| + | |||
| + | '''Решение:''' | ||
| + | |||
Логический квадрат для этого случая имеет вид: | Логический квадрат для этого случая имеет вид: | ||
| Строка 38: | Строка 70: | ||
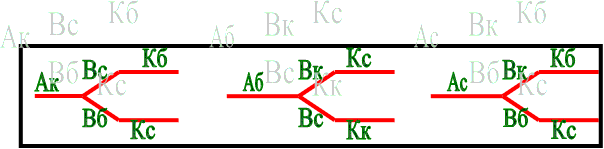
Графы для этой задачи имеют вид. | Графы для этой задачи имеют вид. | ||
| + | |||
| + | [[Изображение:r444.gif]] | ||
И в том, и в другом случае получаем ответ: Валя была в красном платье, Катя – в белом и Аня - в синем. | И в том, и в другом случае получаем ответ: Валя была в красном платье, Катя – в белом и Аня - в синем. | ||
Ребята оценивают достоинства и недостатки каждого из этих способов. | Ребята оценивают достоинства и недостатки каждого из этих способов. | ||
| − | [[Категория:Проект ДООМ]] | + | '''3.''' Подведение итогов. |
| + | |||
| + | '''Домашнее задание:''' | ||
| + | |||
| + | Разбирается дело Брауна, Джонса и Смита. Один из них совершил преступление. В процессе расследования каждый из них сделал два заявления. | ||
| + | |||
| + | Браун: «Я не сделал этого. Джонс не делал этого». | ||
| + | |||
| + | Джонс: «Браун не делал этого. Смит сделал это». | ||
| + | |||
| + | Смит: «Я не делал этого. Браун сделал это». | ||
| + | |||
| + | Было установлено, что один из них дважды солгал; другой дважды сказал правду, третий раз солгал, раз сказал правду. Кто совершил преступление? | ||
| + | |||
| + | Факультативное занятие составила Болонина Л.А. команды 022, г. Казани. для учащихся 7 класса.. | ||
| + | |||
| + | [[Категория:Проект ДООМ 2007-2008 (1 цикл)]] | ||
Текущая версия на 14:46, 10 января 2008
участник: Болонина Людмила Александровна, 022.
Краткое изложение факультативного занятия на тему:
«Применение графов к решению логических задач»
Цель: разобрать закономерности решения логических задач с помощью графов.
Ход занятия:
1) Объяснение учителем.
2) Решение логических задач с помощью графов.
3) Подведение итогов.
4) Домашнее задание.
Основой применения графов для решения логических задач служит выявление и последовательное исключение логических возможностей, задаваемых условиями задач. Это выявление и исключение логических возможностей часто может быть истолковано с помощью построения и рассмотрения соответствующих графов.
Задача 1.
Из трех человек, стоящих рядом, один всегда говорит правду (правдивый), другой всегда лжет (лжец), а третий, смотря по обстоятельствам, говорит правду или ложь («дипломат»). У стоящего слева спросили: «Кто стоит рядом с тобой?» Он ответил: «Правдолюб». Стоящему в центре, задали вопрос: «Кто ты?», и он ответил: «Я дипломат». Когда у стоящего справа спросили: «Кто стоит рядом с тобой?», он ответил: «Лжец». Кто где стоял? Если в данной задаче ребро графа будет соответствовать месту, занимаемому тем или иным человеком, то нам могут представиться следующие возможности.
Решение:
Рассмотрим первую возможность. Если «правдолюб» стоит слева, то рядом с ним, судя по его ответу, находится «правдолюб». У нас же стоит лжец. Рассмотрев таким образом все остальные возможности, мы придем к выводу, что расстановка «дипломат», «лжец», «правдолюб» удовлетворяет задаче. Действительно, если «правдолюб» стоит справа, то, по его ответу, рядом с ним «лжец», что выполняется. Стоящий в центре заявляет, что он «дипломат», и следовательно, лжет, а стоящий справа также лжет. Таким образом все условия задачи выполнены. В качестве задачи второго типа можно предложить следующую.
Задача 2.
В пяти корзинах лежали яблоки пяти разных сортов. Яблоки первого сорта лежат в корзинах Г и Д; яблоки второго сорта - в корзинах А. Б, Г; в корзинах А, Б, В имеются яблоки пятого сорта, в корзине В имеются к тому же яблоки четвертого сорта, а в корзине Д-третьего. Пронумеруйте каждую корзину так, чтобы в корзине №1 были яблоки первого сорта (хотя бы одно); в корзине № 2-второго и т.д.
Решение: Составим граф:
Ответ: №1-Г; №2-А или №2-Б; №3-Д; №4-В; №5-Б или №5-А Возникает вопрос: так ли уж нужны были графы в этой задаче? Разве нельзя прийти к решению логическим путем? Можно, но графы придали условия наглядность, упростили решение.
Задача 3.
В обеденный перерыв предприниматели разговорились, кто сколько газет читает. Выяснилось, что каждый выписывает и читает две и только две газеты, каждую газету читают пять человек, и любая комбинация читается одним человеком. Сколько названий газет выписывают предприниматели? Сколько всего было человек?
Решение:
Решение этой задачи достигается построением следующего графа, где каждая вершина обозначает соответствующую газету и соответственно 5 подписчиков, а каждое ребро будет соответствовать одному подписчику. Суть метода решения этой и подобных ей задач состоит в установлении связей между множеством вершин и множеством ребер графа. Следовательно, в данной задаче предприниматели выписывают шесть наименований газет. Всего предпринимателей: 6*(6-1)/2=15 чел. Полезно решать логические задачи разными методами. Например, следующую задачу можно решить способом логических квадратов и с помощью графов.
Задача 3.
Три ученицы - Аня, Валя. Катя - участвовали в новогоднем бале - маскараде. Одна из них была в красном костюме, другая - в белом, третья - в синем. Если сказать, что Аня была в красном, Валя – не в красном, и Катя –не в синем, то одно из этих утверждений будет верным, а два других –неверными. В каком костюме была каждая из учениц?
Решение:
Логический квадрат для этого случая имеет вид:
Аня Валя Катя Красное 0 1 0 Белое 0 0 1 Синее 1 0 0
Графы для этой задачи имеют вид.
И в том, и в другом случае получаем ответ: Валя была в красном платье, Катя – в белом и Аня - в синем. Ребята оценивают достоинства и недостатки каждого из этих способов.
3. Подведение итогов.
Домашнее задание:
Разбирается дело Брауна, Джонса и Смита. Один из них совершил преступление. В процессе расследования каждый из них сделал два заявления.
Браун: «Я не сделал этого. Джонс не делал этого».
Джонс: «Браун не делал этого. Смит сделал это».
Смит: «Я не делал этого. Браун сделал это».
Было установлено, что один из них дважды солгал; другой дважды сказал правду, третий раз солгал, раз сказал правду. Кто совершил преступление?
Факультативное занятие составила Болонина Л.А. команды 022, г. Казани. для учащихся 7 класса..