Семинар ДООМ "Решение задач на применение теории графов"

Версия 21:59, 3 декабря 2007 (просмотреть исходный код) Denis (обсуждение | вклад) (Новая: '''УРОК №2.''' Тема: Решение задач на применение теории графов. Цели: - повт...)		Текущая версия на 14:49, 10 января 2008 (просмотреть исходный код) Васильева Александра (обсуждение | вклад)
(не показана 1 промежуточная версия 1 участника)
Строка 70:		Строка 70:
	[[Изображение:Urok_2_4.JPG]]		[[Изображение:Urok_2_4.JPG]]
		+
		+	[[Категория:Проект ДООМ 2007-2008 (1 цикл)]]

---

Текущая версия на 14:49, 10 января 2008

                               УРОК №2.

           Тема: Решение задач на применение теории графов.

Цели:
      - повторить основные определения по теории графов;
      - отработка навыков решения задач на применение графов;
      - прививать самостоятельность, учить анализировать, развивать нестандартность мышления;

                                АКТУАЛИЗАЦИЯ:

1).Что называется графом; приведите примеры, где в практической деятельности встречаются графы? 
2).Кому принадлежит первая работа по теории графов? 
3).Какие графы называются полными и неполными? 
4).Как подсчитать количество ребер графа, имеющего n-вершин? 
5).Что называется степенью графа? 
6).Какая вершина называется четной и нечетной? 
7).Какой граф называется однородным? 
8).Чему равна сумма степеней всех вершин графа? 

Задача 1 (устно). Докажите, что не существует графа с пятью вершинами, степени которых 4, 4, 4,2? 

Задача 2. (устно). В одном городе всего 25 телефонов. Можно ли их соединить проводами так,
чтобы каждый телефон был соединен ровно с пятью другими?

                           ОТРАБОТКА НАВЫКОВ РЕШЕНИЯ ЗАДАЧ.

ЗАДАЧА 1. В классе 30 человек. Может ли быть так, что 9 из них имеют по 3 друга в этом классе,
11 – по 4 друга, а 10 – по 5 друзей?

РЕШЕНИЕ: представим граф с тридцатью вершинами, у которого 9 вершин имеют степень 3, 11 – степень 4, 10 – степень 5, следовательно, у этого графа 19 нечетных вершин, что противоречит закономерности: число нечетных вершин графа четно. Значит, не может.

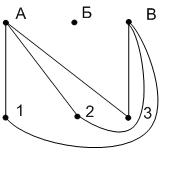
ЗАДАЧА 2. В трех различных домах живут три поссорившихся соседа. Недалеко от их домов 
расположены три колодца. Можно ли от каждого дома провести к каждому из колодцев тропинку так,
чтобы никакие 2 из них не пересекались?

Решение: Построим граф , где дома обозначим буквами А, В, С, а колодцы цифрами 1, 2, 3.

 По рисунку видно, что нельзя.

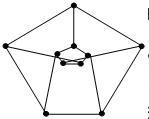
ЗАДАЧА 3. В государстве система авиалиний устроена так, что любой город соединен авиалиниями не более чем с тремя другими и из любого города в любой другой можно проехать, сделав не более одной пересадки. Какое максимальное число городов может быть в этом государстве? РЕШЕНИЕ: построим граф , по которому показаны существующие авиалинии.

Если существует некоторый город N, то из него можно добраться не более, чем до трех городов, а из каждого из них не более чем до двух. Тогда всего городов не более чем 1+3+6=10.

САМОСТОЯТЕЛЬНАЯ РАБОТА ( по вариантам).

1 вариант.

ЗАДАЧА. В государстве 100 городов и из каждого из них выходит 4 дороги. Сколько всего дорог в
государстве?

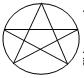
ЗАДАЧА. Можно ли фигуру, изображенную на рисунке, начертить одним росчерком пера? Ответ обоснуйте.

2 вариант.

ЗАДАЧА. В государстве52 города и из каждого выходит 4 дороги. Сколько всего дорог в
государстве?

ЗАДАЧА. Можно ли фигуру, изображенную на рисунке, начертить одним росчерком пера?