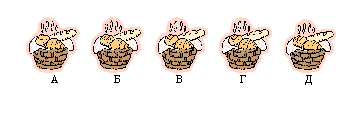Семинар ДООМ. Знакомство с графами (5 класс)
| (не показаны 4 промежуточные версии 1 участника) | |||
| Строка 1: | Строка 1: | ||
[[Участник: Пенкина Любовь Ивановна]] | [[Участник: Пенкина Любовь Ивановна]] | ||
| − | '''Тема: '''Графы'''''' | + | <h2><font color="#DB7093">'''Тема: '''Графы''''''</font></h2> |
<b>Цель:</b> <br> | <b>Цель:</b> <br> | ||
| Строка 57: | Строка 57: | ||
Графами мы пользуемся довольно часто. Возьмите схему железных дорог: здесь станции – это вершины графа, перегоны (участки пути между станциями) – ребра графа. Вершины и ребра многогранни-ка (куба, пирамиды и т.д.) тоже образуют граф. | Графами мы пользуемся довольно часто. Возьмите схему железных дорог: здесь станции – это вершины графа, перегоны (участки пути между станциями) – ребра графа. Вершины и ребра многогранни-ка (куба, пирамиды и т.д.) тоже образуют граф. | ||
| − | '''IV. Решение первых трех задач''' | + | '''IV. Решение первых трех задач'''<br> |
[[Изображение:ris5.gif]]<br><br> | [[Изображение:ris5.gif]]<br><br> | ||
| − | А теперь решим первые три задачи с помощью графов. | + | А теперь решим первые три задачи с помощью графов.<br> |
| − | Попробуем построить граф для ситуации, описанной в задаче 8.1: «Кто играет Ляпкина-Тяпкина?» Изобразим юных актеров кружками верхнего ряда: А — Алик, Б — Боря, В — Вова, Г — Гена, Д — Дима, а роли, которые они собираются играть – кружками второго ряда | + | Попробуем построить граф для ситуации, описанной в задаче 8.1: <br>«Кто играет Ляпкина-Тяпкина?» Изобразим юных актеров кружками верхнего ряда:<br>А — Алик, <br>Б — Боря,<br>В — Вова, <br>Г — Гена,<br>Д — Дима, <br>а роли, которые они собираются играть – кружками второго ряда:<br>1— Ляпкин-Тяпкин, <br>2 — Хлестаков,<br>3 — Осип, <br>4 — Земляника,<br>5 — Городничий. <br>Затем от каждого участника проведем отрезки, т. е. ребра, к ролям, которые он хотел бы сыграть. <br>У нас получится граф с десятью вершинами и десятью ребрами.<br> |
| − | Чтобы решить задачу, нужно из десяти выбрать пять ребер, не имеющих общих вершин. Сделать это легко. Достаточно заметить, что в вершины 3 и 4 ведет по одному ребру, из вершин Д и В соответственно. Это означает, что Осипа (вершина 3) должен играть Дима (кто же еще?), а Землянику — Вова. Вершина 1 — Ляпкин-Тяпкин — соединена ребрами с Г и Д. Ребро 1 — Д отпадает, так как Дима уже занят, остается ребро 1 — Г, Ляпкина-Тяпкина должен играть Гена. Остается соединить вершины А и Б с вершинами 2 и 5, соответствующими ролям Хлестакова и Городничего. Это можно сделать двумя способами: либо выбрать ребра А — 5 и Б — 2, либо ребра А—2 и Б — 5. В первом случае Алик будет играть Городничего, а Боря — Хлестакова, во втором случае наоборот. Как показывает наш граф, других решений задача не имеет. | + | Чтобы решить задачу, нужно из десяти выбрать пять ребер, не имеющих общих вершин. Сделать это легко. Достаточно заметить, что в вершины 3 и 4 ведет по одному ребру, из вершин Д и В соответственно. Это означает, что Осипа (вершина 3) должен играть Дима (кто же еще?), а Землянику — Вова. Вершина 1 — Ляпкин-Тяпкин — соединена ребрами с Г и Д. Ребро 1 — Д отпадает, так как Дима уже занят, остается ребро 1 — Г, Ляпкина-Тяпкина должен играть Гена. <br>Остается соединить вершины А и Б с вершинами 2 и 5, соответствующими ролям Хлестакова и Городничего. Это можно сделать двумя способами: либо выбрать ребра А — 5 и Б — 2, либо ребра А—2 и Б — 5. В первом случае Алик будет играть Городничего, а Боря — Хлестакова, во втором случае наоборот. Как показывает наш граф, других решений задача не имеет.<br> |
| − | Постройте теперь графы для второй и третьей задач. У вас получились те же графы! Теперь вы видите, что вторая и третья задачи по сути ничем не отличаются от первой. Отметив на этих графах по пять ребер, не имеющих общих вершин, вы тем самым решите данные задачи. | + | Постройте теперь графы для второй и третьей задач. <br>У вас получились те же графы! Теперь вы видите, что вторая и третья <br>задачи по сути ничем не отличаются от первой. Отметив на этих графах по пять ребер,<br> не имеющих общих вершин, вы тем самым решите данные задачи. <br> |
| − | Возникает вопрос: так ли уж нужны были графы в разобранных задачах? Разве нельзя прийти к решению чисто логическим путем? Да, можно. Но графы придали условиям наглядность, упростили решение и выявили сходство задач, превратив три задачи в одну, а это не так уж мало. А теперь представьте себе задачи, графы которых имеют 100 или более вершин. А ведь именно такие задачи приходится решать современным инженерам и экономистам. Тут уж без графов не обойтись. | + | Возникает вопрос: так ли уж нужны были графы в разобранных задачах? <br>Разве нельзя прийти к решению чисто логическим путем? Да, можно. Но графы придали условиям наглядность,<br> упростили решение и выявили сходство задач, превратив три задачи в одну, а это не так уж мало. <br>А теперь представьте себе задачи, графы которых имеют 100 или более вершин.<br> А ведь именно такие задачи приходится решать современным инженерам и экономистам. Тут уж без графов не обойтись.<br> |
| − | + | Ceйчас почти в любой отрасли науки и техники встречаешься с графами: в электротехнике — при построении электрических схем,<br> в химии и биологии — при изучении молекул и их цепочек, в экономике — при решении задач о выборе оптимального пути <br>для потоков грузового транспорта и во многих других задачах. <br>О математике и говорить не приходится. С теорией графов связаны не только математические развлечения и головоломки, <br>но и такие серьезные науки, как теория отношений и теория групп.<br> | |
| − | И все же теория графов — наука сравнительно молодая: во времена Ньютона такой науки еще не было, хотя и были в ходу «генеалогические деревья», представляющие собой разновидности графов. Первая работа по теории графов принадлежит Леонарду Эйлеру, и появилась она в 1736 году в публикациях Петербургской Академии наук. Начиналась эха работа с рассмотрения следующей задачи: | + | И все же теория графов — наука сравнительно молодая: во времена Ньютона такой науки еще не было, хотя и были в <br>ходу «генеалогические деревья», представляющие собой разновидности графов. Первая работа по теории графов принадлежит <br>Леонарду Эйлеру, и появилась она в 1736 году в публикациях Петербургской Академии наук.<br> Начиналась эха работа с рассмотрения следующей задачи:<br> |
[[Изображение:ris6.gif]]<br><br> | [[Изображение:ris6.gif]]<br><br> | ||
| − | '''Задача о кенигсбергских мостах'''. Город Кенигсберг (ныне Калининград) расположен на берегах и двух островах реки Прегель (Преголи). Различные части города были соединены семью моста¬ми, как пока-зано на рисунке В воскресные дни горожане совер¬шают прогулки по городу. Можно ли выбрать такой маршрут, чтобы пройти один и только один раз по каждому мосту и потом вернуться в начальную точку пути? | + | '''Задача о кенигсбергских мостах'''.<br> Город Кенигсберг (ныне Калининград) расположен на берегах и двух островах реки Прегель (Преголи). Различные части города были соединены семью моста¬ми, как пока-зано на рисунке В воскресные дни горожане совер¬шают прогулки по городу. Можно ли выбрать такой маршрут, чтобы пройти один и только один раз по каждому мосту и потом вернуться в начальную точку пути?<br> |
| − | ''Обсуждение.'' Обозначим различные части города буквами А, В, C ,D, а мосты — буквами a,b,c, d, e ,f, g. В этой задаче существенны лишь переходы через мосты: переходя через любой мост, мы всегда из одной части города попадаем в другую, - и, наоборот, переходя из одной части города в другую, мы непременно пройдем по мосту. Поэтому изобразим план города в виде графа, вершины которого А, В, С и D изображают отдельные части города, а ребра а, b9 с, d, e, f, g — мосты, соединяющие соответствующие части города. Если бы существовал маршрут, удовлетворяющий условию задачи, то существовал бы замкнутый и непрерывный обход этого графа, проходящий один раз по каждому ребру. Иными словами, этот граф можно было бы вычертить, не отрывая карандаша от бумаги и не проходя дважды по одному и тому же ребру. Но это невозможно — какую бы вершину мы ни выбрали за исходную, нам придется проходить через остальные вершины, и при этом каждому «входящему» ребру (мосту, по которому мы вошли в эту часть города) будет соответствовать «выходящее» ребро (мост, которым мы воспользуемся затем, чтобы покинуть эту часть | + | ''Обсуждение.''<br> Обозначим различные части города буквами А, В, C ,D, а мосты — буквами a,b,c, d, e ,f, g. В этой задаче существенны лишь переходы через мосты: переходя через любой мост, мы всегда из одной части города попадаем в другую, - и, наоборот, переходя из одной части города в другую, мы непременно пройдем по мосту. Поэтому изобразим план города в виде графа, вершины которого А, В, С и D изображают отдельные части города, а ребра а, b9 с, d, e, f, g — мосты, соединяющие соответствующие части города. <br>Если бы существовал маршрут, удовлетворяющий условию задачи, то существовал бы замкнутый и непрерывный обход этого графа, проходящий один раз по каждому ребру. Иными словами, этот граф можно было бы вычертить, не отрывая карандаша от бумаги и не проходя дважды по одному и тому же ребру. Но это невозможно — какую бы вершину мы ни выбрали за исходную, нам придется проходить через остальные вершины, и при этом каждому «входящему» ребру (мосту, по которому мы вошли в эту часть города) будет соответствовать «выходящее» ребро (мост, которым мы воспользуемся затем, чтобы покинуть эту часть города): число ребер, входящих в каждую вершину, будет равно числу ребер, выходящих из нее, т. е. общее число ребер, сходящихся в каждой вершине, должно быть четным. <br>Наш граф этому условию не удовлетворяет, и поэтому требуемого маршрута не существует. Если в каждой вершине связного графа сходится четное число ребер, то такой граф называется «эйлеров». Можно доказать, что всякий ''эйлеров граф'' допускает непрерывный замкнутый обход (такой путь в теории графов называется ''ц и к л о м''), проходящий по каждому ребру ровно один раз. Из предыдущих рассуждений следует, что граф, не являющийся эйлеровым, такого обхода не допускает.<br><br> |
| − | '''V. Закрепление''' полученных навыков решения задач с помощью графов. | + | '''V. Закрепление''' полученных навыков решения задач с помощью графов.<br> |
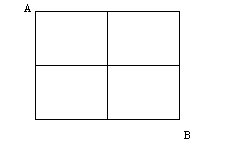
| − | 1. Сколькими способами можно пройти из А в В, двигаясь по линиям слева направо и сверху вниз? | + | 1. Сколькими способами можно пройти из А в В, двигаясь по линиям слева направо и сверху вниз? <br> |
[[Изображение:ris7.gif]]<br><br> | [[Изображение:ris7.gif]]<br><br> | ||
| Строка 109: | Строка 109: | ||
Итак, сегодня мы познакомились еще с одним из способов решения задач. Таким образом, чтобы ответить на вопрос задачи, нужно найти наиболее оптимальный способ решения. | Итак, сегодня мы познакомились еще с одним из способов решения задач. Таким образом, чтобы ответить на вопрос задачи, нужно найти наиболее оптимальный способ решения. | ||
| − | [[Категория:Проект ДООМ]] | + | [[Категория:Проект ДООМ 2007-2008 (1 цикл)]] |
Текущая версия на 15:01, 10 января 2008
Участник: Пенкина Любовь Ивановна
'Тема: Графы'
Цель:
знакомство с новым способом решения задач повышенной трудности;
развитие логического мышления у учащихся;
воспитание интереса к предмету.
Оборудование:
карточки с задачами;
многогранники: куб, пирамида, додекаэдр;
школьная доска с готовыми рисунками графов.
Ход занятия.
I. Вводная беседа
Сегодня мы с вами познакомимся еще с одним способом решения логических задач. Рассмотрим сначала три задачи:
1. Кто играет Ляпкина-Тяпкина?
В школьном драмкружке решили ставить гоголевского «Ревизора». И тут разгорелся жаркий спор. Все началось с Ляпкина-Тяпкина. - Ляпкиным-Тяпкиным буду я! – решительно заявил Гена. - Нет, я буду Ляпкиным-Тяпкиным, - возразил Дима. – С раннего детства мечтал воплотить этот образ на сцене. - Ну, хорошо, согласен уступить эту роль, если мне дадут сыграть Хлестакова, - проявил великодушие Гена. - …А мне – Осипа – не уступил ему в великодушии Дима. - Хочу быть Земляникой или Городничим, - сказал Вова. - Нет, Городничим буду я, - хором закричали Алик и Боря. – Или Хлестаковым, - добавили они одновременно. Удастся ли распределить роли так, чтобы исполнители были довольны? (Мы не спрашиваем, будут ли довольны зрители.)
2. Сварливые соседи.
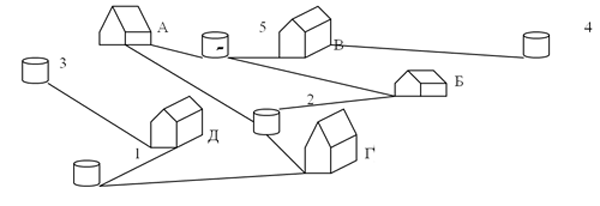
Житель пяти домов поссорились друг с другом и, чтобы не встречаться у колодцев, решили поделить их (колодцы) так,
чтобы хозяин каждого дома ходил к «своему» колодцу по «своей» тропинке. Удастся ли им это сделать?
В пяти корзинах лежат хлебцы пяти сортов. Хлебцы первого сорта лежат в корзинах Г и Д; хлебцы второго сорта – в корзинах А,
Б и Г; в корзинах А, Б и В имеются хлебцы пятого сорта, в корзине В имеются к тому же хлебцы четвертого сорта, а в корзине
Д – третьего. Требуется дать каждой корзине номер, но так, чтобы в корзине № 1 были хлебцы первого сорта (хотя бы один), в
корзине № 2 – второго и т.д.
II. Обсуждение.
Эти задачи довольно простые. Достойно удивления другое – хотя на первый взгляд эти задачи различны – в одной говорится о
распределении ролей, в другой – о тропинках от домов к колодцам, в третьей – о нумерации корзин с хлебцами, существует
единый подход к решению этих задач, связанный с так называемой теорией графов.
Переведя эти задачи на язык теории графов, вы увидите, что все три задачи превратятся в простенькую задачу «на графы».
Познакомимся с основными понятиями теории графов. Прежде всего, стоит сказать о том, что гра-фы, о которых идет речь, к
аристократам былых времен никакого отношения не имеют. Наши «графы» имеют корнем греческое слово «графо», что
значит «пишу». Тот же корень в словах «график», «биография», «голография»
Понятие графа проще всего выяснить на примере.
'III. Разбор задач.
4. Первенство классов.
В первенстве класса по настольному теннису принимали участие 6 учеников: Андрей, Борис, Виктор, Галина, Дмитрий и
Елена. Первенство проводится по круговой системе – каждый из участников играет с каждым из остальных один раз. К
настоящему моменту некоторые игры уже проведены: Анд-рей сыграл с Борисом, Галиной и Еленой; Борис, как уже говорилось, с
Андреем и еще с Галиной; Виктор – с Галиной, Дмитрием и Еленой; Галина – с Андреем и Виктором. Сколько игр проведено к
настоящему моменту и сколько еще осталось?
О б с у ж д е н и е.
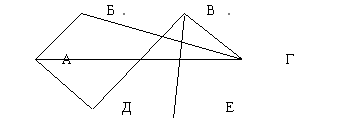
Изобразим данные задачи в виде схемы. Участников будем изображать точками: Андрея –
точкой А, Бориса – точкой Б и т.д. Если двое участников уже сыграли между собой, то будем соединять изображающие их точки
отрезками. Получается схема, показанная на рисунке.
Такие схемы называются графами. Точки А, Б, В, Г, Д называются вершинами графа, соединяющие их отрезки – ребрами графа. Заметьте, что точки пересечения ребер графа не являются его вершинами. Во избежание путаницы вершины графа часто изображают не точками, а кружочками. Ребра зачастую оказывается удобнее изображать не прямолинейными отрезками, а криволинейными – «дугами». Решим нашу задачу. Число игр, проведенных к настоящему моменту, равно числу ребер, т.е. 7. Чтобы найти число игр, которые осталось провести, построим еще один граф с теми же вершинами, но ребрами будем соединять тех участников, которые еще не играли друг с другом. Ребер у этого графа оказалось 8, значит, осталось провести 8 игр.
Графами мы пользуемся довольно часто. Возьмите схему железных дорог: здесь станции – это вершины графа, перегоны (участки пути между станциями) – ребра графа. Вершины и ребра многогранни-ка (куба, пирамиды и т.д.) тоже образуют граф.
А теперь решим первые три задачи с помощью графов.
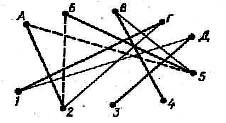
Попробуем построить граф для ситуации, описанной в задаче 8.1:
«Кто играет Ляпкина-Тяпкина?» Изобразим юных актеров кружками верхнего ряда:
А — Алик,
Б — Боря,
В — Вова,
Г — Гена,
Д — Дима,
а роли, которые они собираются играть – кружками второго ряда:
1— Ляпкин-Тяпкин,
2 — Хлестаков,
3 — Осип,
4 — Земляника,
5 — Городничий.
Затем от каждого участника проведем отрезки, т. е. ребра, к ролям, которые он хотел бы сыграть.
У нас получится граф с десятью вершинами и десятью ребрами.
Чтобы решить задачу, нужно из десяти выбрать пять ребер, не имеющих общих вершин. Сделать это легко. Достаточно заметить, что в вершины 3 и 4 ведет по одному ребру, из вершин Д и В соответственно. Это означает, что Осипа (вершина 3) должен играть Дима (кто же еще?), а Землянику — Вова. Вершина 1 — Ляпкин-Тяпкин — соединена ребрами с Г и Д. Ребро 1 — Д отпадает, так как Дима уже занят, остается ребро 1 — Г, Ляпкина-Тяпкина должен играть Гена.
Остается соединить вершины А и Б с вершинами 2 и 5, соответствующими ролям Хлестакова и Городничего. Это можно сделать двумя способами: либо выбрать ребра А — 5 и Б — 2, либо ребра А—2 и Б — 5. В первом случае Алик будет играть Городничего, а Боря — Хлестакова, во втором случае наоборот. Как показывает наш граф, других решений задача не имеет.
Постройте теперь графы для второй и третьей задач.
У вас получились те же графы! Теперь вы видите, что вторая и третья
задачи по сути ничем не отличаются от первой. Отметив на этих графах по пять ребер,
не имеющих общих вершин, вы тем самым решите данные задачи.
Возникает вопрос: так ли уж нужны были графы в разобранных задачах?
Разве нельзя прийти к решению чисто логическим путем? Да, можно. Но графы придали условиям наглядность,
упростили решение и выявили сходство задач, превратив три задачи в одну, а это не так уж мало.
А теперь представьте себе задачи, графы которых имеют 100 или более вершин.
А ведь именно такие задачи приходится решать современным инженерам и экономистам. Тут уж без графов не обойтись.
Ceйчас почти в любой отрасли науки и техники встречаешься с графами: в электротехнике — при построении электрических схем,
в химии и биологии — при изучении молекул и их цепочек, в экономике — при решении задач о выборе оптимального пути
для потоков грузового транспорта и во многих других задачах.
О математике и говорить не приходится. С теорией графов связаны не только математические развлечения и головоломки,
но и такие серьезные науки, как теория отношений и теория групп.
И все же теория графов — наука сравнительно молодая: во времена Ньютона такой науки еще не было, хотя и были в
ходу «генеалогические деревья», представляющие собой разновидности графов. Первая работа по теории графов принадлежит
Леонарду Эйлеру, и появилась она в 1736 году в публикациях Петербургской Академии наук.
Начиналась эха работа с рассмотрения следующей задачи:
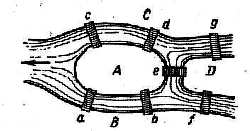
Задача о кенигсбергских мостах.
Город Кенигсберг (ныне Калининград) расположен на берегах и двух островах реки Прегель (Преголи). Различные части города были соединены семью моста¬ми, как пока-зано на рисунке В воскресные дни горожане совер¬шают прогулки по городу. Можно ли выбрать такой маршрут, чтобы пройти один и только один раз по каждому мосту и потом вернуться в начальную точку пути?
Обсуждение.
Обозначим различные части города буквами А, В, C ,D, а мосты — буквами a,b,c, d, e ,f, g. В этой задаче существенны лишь переходы через мосты: переходя через любой мост, мы всегда из одной части города попадаем в другую, - и, наоборот, переходя из одной части города в другую, мы непременно пройдем по мосту. Поэтому изобразим план города в виде графа, вершины которого А, В, С и D изображают отдельные части города, а ребра а, b9 с, d, e, f, g — мосты, соединяющие соответствующие части города.
Если бы существовал маршрут, удовлетворяющий условию задачи, то существовал бы замкнутый и непрерывный обход этого графа, проходящий один раз по каждому ребру. Иными словами, этот граф можно было бы вычертить, не отрывая карандаша от бумаги и не проходя дважды по одному и тому же ребру. Но это невозможно — какую бы вершину мы ни выбрали за исходную, нам придется проходить через остальные вершины, и при этом каждому «входящему» ребру (мосту, по которому мы вошли в эту часть города) будет соответствовать «выходящее» ребро (мост, которым мы воспользуемся затем, чтобы покинуть эту часть города): число ребер, входящих в каждую вершину, будет равно числу ребер, выходящих из нее, т. е. общее число ребер, сходящихся в каждой вершине, должно быть четным.
Наш граф этому условию не удовлетворяет, и поэтому требуемого маршрута не существует. Если в каждой вершине связного графа сходится четное число ребер, то такой граф называется «эйлеров». Можно доказать, что всякий эйлеров граф допускает непрерывный замкнутый обход (такой путь в теории графов называется ц и к л о м), проходящий по каждому ребру ровно один раз. Из предыдущих рассуждений следует, что граф, не являющийся эйлеровым, такого обхода не допускает.
V. Закрепление полученных навыков решения задач с помощью графов.
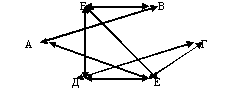
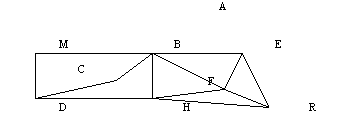
1. Сколькими способами можно пройти из А в В, двигаясь по линиям слева направо и сверху вниз?
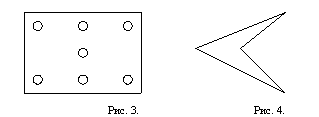
2. В выходной день Миша решил навестить своих друзей: Алешу, Борю, Витю, Гену, Диму, Женю, Колю, Славу. Он начертил схему взаимного расположения домов, где живут мальчики, и дорог, соеди-няющих их. Посетил он их в следующем порядке: Алеша, Боря, Витя, Гена, Дима, Женя, Коля, Слава. Ус-тановите, какой дом кому принадлежит, если ни к одному из домов Миша не подходил более одного раза, Известно, что Миша живет в доме М, последним он посетил дом R.
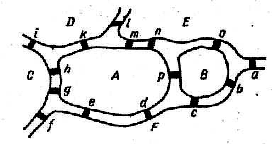
3. Задача Леонарда Эйлера. Можно ли совершить прогулку по городу, план которого показан на рисунке, пройдя в точности один раз по каждому из пятнадцати мостов. Возвращаться в начальную точку пути не обязательно. Если такой обход существует, найти его, указав мосты в той последовательности, в которой вы их проходите. Если же такого обхода не может существовать, объясните, почему не может. Постройте граф — план города.
VI. Задание на дом.
1. Решение задач на разрезание
№ 1. Разрезать фигуру на четыре равные части (рис. 1):
№ 2. Пусть фигура состоит из трех равных квадратов, расположенных так, как показано на рис. 2. Вырезать из этой фигуры такую часть, чтобы приложив ее к оставшейся части, получить квадрат, внутри которого имеется квадратное отверстие.
№ 3. Квадрат с вырезанной «четвертушкой» легко разрезать на четыре равные части (см. рис. 1). А сможете ли вы разрезать сам квадрат на пять равных частей?
№ 4. На коврике изображено семь роз. Требуется тремя прямыми линиями разрезать коврик на семь частей, каждая из которых содержала бы по одной розе (рис. 3).
№ 5. Произвольный треугольник АВС разрезать на три части – такие, чтобы из них можно было со-ставить прямоугольник.
№ 6. Изображенную на рис. 4 фигуру требуется разделить на шесть частей, проведя всего лишь две прямые. Попытайтесь это сделать.
VII. Итог занятия.
Итак, сегодня мы познакомились еще с одним из способов решения задач. Таким образом, чтобы ответить на вопрос задачи, нужно найти наиболее оптимальный способ решения.