Семинар ДООМ. Основные понятия теории графов.
| (не показана 1 промежуточная версия 1 участника) | |||
| Строка 23: | Строка 23: | ||
а отрезками - их соединяющие маршруты. Получается следующий чертеж: (рис.1) | а отрезками - их соединяющие маршруты. Получается следующий чертеж: (рис.1) | ||
| − | [[Изображение: | + | [[Изображение:riss1.gif]] |
| Строка 97: | Строка 97: | ||
(рис.2) | (рис.2) | ||
| − | [[Изображение: | + | [[Изображение:riss2.gif]] |
Рассмотрим задачу, которую легко можно решить, используя теорию графов. | Рассмотрим задачу, которую легко можно решить, используя теорию графов. | ||
| Строка 116: | Строка 116: | ||
| − | [[Изображение: | + | [[Изображение:riss4,5.gif]] (рис. 4) (рис.5) |
| Строка 133: | Строка 133: | ||
'''РЕШЕНИЕ:''' (рис.6) | '''РЕШЕНИЕ:''' (рис.6) | ||
| − | [[Изображение: | + | [[Изображение:riss6.gif]] |
Изобразим данные задачи в виде схемы. Участники – это точки, сплошные линии – это сыгранные партии, | Изобразим данные задачи в виде схемы. Участники – это точки, сплошные линии – это сыгранные партии, | ||
| Строка 156: | Строка 156: | ||
Урок составила Трифонова В.А. команды 022, г. Казани. Этот урок можно провести как в 5, так и в 11 классах, так как он вводит ребят в теорию графов. | Урок составила Трифонова В.А. команды 022, г. Казани. Этот урок можно провести как в 5, так и в 11 классах, так как он вводит ребят в теорию графов. | ||
| − | [[Категория:Проект ДООМ]] | + | [[Категория:Проект ДООМ 2007-2008 (1 цикл)]] |
Текущая версия на 15:04, 10 января 2008
участник: Трифонова Валентина Артемьевна, 022.
ЦЕЛИ:
познакомиться с определением графов и его сопутствующими понятиями;
разобрать закономерности, по которым строятся графы и с помощью них решаются логические задачи;
прививать самостоятельность, нестандартность мышления, интерес к математике.
ХОД УРОКА:
Рассмотрим следующую задачу:
Между планетами введено космическое сообщение по следующим маршрутам: З-К, П-В, З-П, П-К, У-М, М-С, С-Ю, Ю-М, М-У. Можно ли добраться с З до М?
РЕШЕНИЕ: Попробуем решить эту задачу графически, изобразим схему-чертеж маршрутов,
где точками обозначим названия пунктов З, К, П, В и т.д,
а отрезками - их соединяющие маршруты. Получается следующий чертеж: (рис.1)
Глядя на него можно ответить, что от З до М добраться нельзя.
Ребята мы решили эту задачу с помощью графов.
ОПРЕДЕЛЕНИЕ:
ГРАФОМ называются схемы, состоящие из точек (вершины графов) и соединяющих эти точки отрезков,
прямых или кривых (ребра графов).
Приведите примеры, где в жизни мы встречаемся с графами?
(схемы маршрутов рейсовых автобусов, городской метрополитен, элементы электрических цепей и т.д.)
Графы упрощают решение многих логических задач, экономических, физических и других.
Графы имеют разные виды: их можно изобразить в виде геометрической фигуры, прямоугольника, окружности, овала, в виде дерева,
в виде леса, в виде плоской фигуры.
Рассмотрим процесс соединения вершин графа ребрами.
Схема, состоящая из изолированных вершин, несоединенных ребрами, называется нулевым графом.
Графы, в которых не построены все возможные ребра, называется неполным.
Графы, в которых построены все возможные ребра , называется полным.
В полном графе число ребер равно: n(n-1)\2, где n-число вершин графа.
Каждая вершина в графе имеет свою степень. Степенью вершины графа называется число, соответствующее количеству ребер графа,
исходящих из данной вершины. Вершина называется четной, если степень этой вершины четная и нечетной, если она нечетная.
Сформулируем некоторые закономерности, присущие определенным графам:
1) Степени вершин полного графа одинаковы, и каждая из них на 1 меньше числа вершин этого графа.
2) Сумма степеней вершин графа число четное, равное удвоенному числу ребер графа. Эта закономерность справедлива для любого графа.
3) Если степени всех вершин графа равны, то граф называется однородным.
4) Число нечетных вершин любого графа четно.
5) Невозможно начертить граф с нечетным числом нечетных вершин.
6) Если все вершины графа четные, то можно не отрывая карандаш от бумаги, проведя по каждому ребру только один раз, начертить этот граф, причем движение можно начать с любой вершины. Такой граф называется уникурсальным.
7) Граф, имеющий две нечетные вершины, можно начертить, не отрывая карандаша от бумаги, начав движение с одной из нечетных вершин.
8) Граф, имеющий более двух нечетных вершин, невозможно начертить, не отрывая карандаша от бумаги.
Разберем еще некоторые понятия, необходимые для решения задач, используя графы.
Путем в графе от одной вершины до другой называется такая последовательность ребер, соединяющих вершины,
что никакое ребро при движении не повторяется дважды.
Циклом называется путь, в котором начало и конец совпадают. Если все вершины графа имеют разную степень, то такой цикл
называется элементарным. Если цикл, включает в себя все ребра по одному разу, то цикл называется Эйлеровой линией.
Две вершины графа называются связными, если в графе существует путь с концами в этих вершинах. Если такого пути нет ,
то граф несвязный.
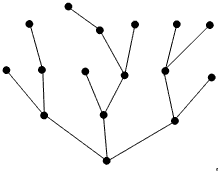
Деревом называется любой связный граф , не имеющий циклов.
Для каждой пары вершин дерева существует единственный путь, их соединяющий. (рис.2)
Рассмотрим задачу, которую легко можно решить, используя теорию графов.
ЗАДАЧА.
Красный, синий, желтый и зеленый карандаши лежат в четырех коробках по одному. Цвет карандаша отличается от цвета коробки.
Известно, что зеленый карандаш лежит в синей коробке, а красный не лежит в желтой. В какой коробке лежит каждый карандаш?
РЕШЕНИЕ:
обозначим точками карандаши и коробки. Сплошная линия будет обозначать, что карандаш лежит в соответствующей коробке,
пунктирная – не лежит.(рис 4). Затем достраиваем граф по следующему правилу: т.к. в коробке лежит только один карандаш,
то из каждой точки должны выходить одна сплошная и три пунктирные линии. (рис5), который и дает решение задачи.
Файл:Riss4,5.gif (рис. 4) (рис.5)
Для следующей задачи постройте граф, соответствующей решению задачи.
ЗАДАЧА.
В первенстве по теннису принимали участие 6 ребят: Андрей, Борис, Виктор, Галина, Дмитрий и Елена.
Первенство проводилось по круговой схеме: каждый из участников играет с каждым из остальных один раз.
Некоторые игры уже проведены: Андрей играл с Борисом, Галиной и Еленой, Виктор с Галиной, Дмитрием и Еленой.
Сколько пар проведено и сколько еще осталось?
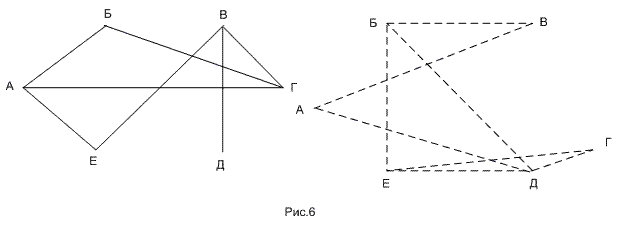
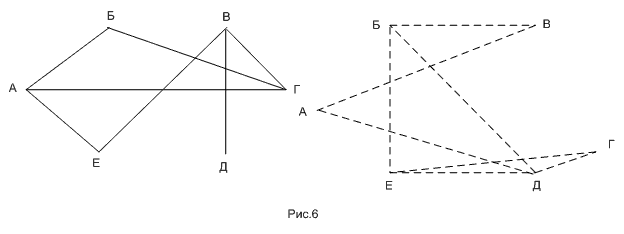
РЕШЕНИЕ: (рис.6)
Изобразим данные задачи в виде схемы. Участники – это точки, сплошные линии – это сыгранные партии,
пунктирные линии – это несыгранные партии. Следовательно , проведено 7 игр, осталось провести – 8 игр.
ДОМАШНЕЕ ЗАДАНИЕ:
Решите с помощью графов.
ЗАДАЧА: В семье четверо детей, им - 5, 8, 13, 15 лет, а зовут их Таня, Юра, Света и Лена.
Одна девочка ходит в детский сад, Таня старше Юры, а сумма лет Тани и Светы делится на три. Сколько лет Лене?
Ответ: Юре – 8 лет, Тане – 13 лет, Свете -5 лет, Лене – 15 лет.
Урок составила Трифонова В.А. команды 022, г. Казани. Этот урок можно провести как в 5, так и в 11 классах, так как он вводит ребят в теорию графов.