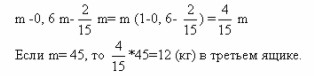Семинар ДООМ: Практическое применение «Теории графов»

Текущая версия на 15:11, 10 января 2008

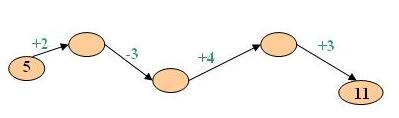
«Графы» нашли широкое применение в различных областях науки. В школьном курсе математики «Графы» встречаются с первого класса, когда детям предлагают, например, найти «потерявшееся число».

Пример:

Далее они встречаются все чаще и чаще, но само определение графа не дается. А жаль! Я думаю, детям интересно было бы познакомиться с этим понятием, научиться применять графы для решения задач. Конечно, каждый учитель может самостоятельно рассказать ребятам об Эйлере, о его исследованиях в области теории граф, да и сами учащиеся могли бы представить эту информацию в виде доклада или компьютерной презентации. Надо об этом подумать!!!

Графы - это не только схемы, к графам еще можно отнести и таблицы, с которыми дети встречаются еще в детском саду.

Когда я с детьми разбирала тему «Графы», мы изучали теорию, решали задачи и приводили примеры из жизни, отвечали на вопрос «Что можно изобразить в виде графа?», то учащиеся выяснили для себя, что практически любой пример или можно решить с помощью графа, или, изобразив граф, найти то или иное решение задачи. Они вспомнили, что в 5 классе у них была тема, где они решали примеры, используя блок- схемы (те же графы).

Сейчас они в 6 классе, но некоторые примеры предпочитают изображать в виде графа.

Пример:

Решение:

Так же задачи на скорость, время, расстояние; задачи на работу; задачи на движение по воде и те задачи, которые решаются через уравнение, тоже можно решить с помощью графа, только этот граф будет представлен в виде таблицы.

А можно одну и ту же задачку оформить по-разному:

Пример:

Гвозди, масса которых m кг, разложили в три ящика. В первый ящик положили 0,6 всех гвоздей, а во второй всех гвоздей. Сколько килограммов гвоздей положили в третий ящик? Найдите значение получившегося выражения при m=45.

Решение:

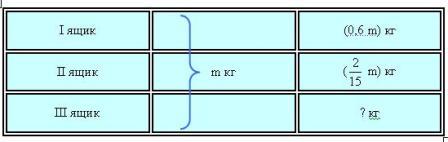
1 способ: (в виде таблицы)

Из таблицы легко составить выражение, упростив которое мы без труда найдем значение выражения:

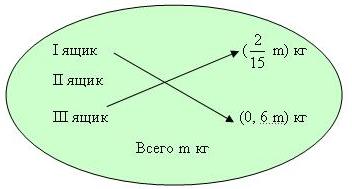
2 способ:(в виде направленного графа)

Таким образом, графы позволяют наглядно показать решение какой- либо задачи. А наглядность в свою очередь помогает лучше усвоить материал.