"Семинар ДООМ" Решение логических задач с помощью графов.
(Новая: Тема урока: «Решение логических задач с помощью графов». Класса: 6. Цель: Ввести понятие «графа», научи...) |
|||
| Строка 7: | Строка 7: | ||
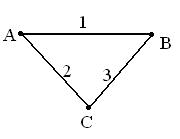
Будем решать эту задачу графически. Вначале отметим точки А и В и соединим их отрезком. Точками будем изображать мальчиков, а отрезок будет означать рукопожатие. Добавим еще одну точку С и соединим её с точками А и В. Всего получается три отрезка. | Будем решать эту задачу графически. Вначале отметим точки А и В и соединим их отрезком. Точками будем изображать мальчиков, а отрезок будет означать рукопожатие. Добавим еще одну точку С и соединим её с точками А и В. Всего получается три отрезка. | ||
| − | + | [[Изображение:Рисую_1.JPG]] | |
Отметим следующую точку Д и соединим её отрезками с тремя точками А, В и С. Теперь уже получилось шесть отрезков. Наконец, отметим пятую точку Е и соединим её со всеми точками, отмеченными ранее. Получилось 10 отрезков, т. е 10 рукопожатий. Значит, на вокзале встретились 5 мальчиков. (Так как урок проходит в 6 классе, то можно проводить его с элементами игры, т. е. предложить ребятам проверить решение на практике. Вызвать к доске сначала 2, затем 3, 4 и 5 учащихся и попросить их пожать друг другу руки. Весь класс сможет убедиться, что всего было 10 рукопожатий.) | Отметим следующую точку Д и соединим её отрезками с тремя точками А, В и С. Теперь уже получилось шесть отрезков. Наконец, отметим пятую точку Е и соединим её со всеми точками, отмеченными ранее. Получилось 10 отрезков, т. е 10 рукопожатий. Значит, на вокзале встретились 5 мальчиков. (Так как урок проходит в 6 классе, то можно проводить его с элементами игры, т. е. предложить ребятам проверить решение на практике. Вызвать к доске сначала 2, затем 3, 4 и 5 учащихся и попросить их пожать друг другу руки. Весь класс сможет убедиться, что всего было 10 рукопожатий.) | ||
| Строка 13: | Строка 13: | ||
| − | + | Графы помогают решать некоторые задачи. Разберем одну из них. | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | Встретились три подруги: Белова, Краснова и Чернова. На одной из них было надето черное платье, на другой – красное, а на третьей белое. Девочка в красном платье говорит Черновой: « Нам надо поменяться платьями, а то цвет наших платьев не соответствует нашим фамилиям». Кто из девочек в какое платье был одет? | |
| − | + | ||
| − | + | ||
| − | |||
| − | |||
Решение. Здесь мы имеем два равночисленных множества: множество фамилий и множество цветов платьев. Между этими множествами надо установить взаимно-однозначное соответствие. Для этого построим граф. Пусть белые кружочки Б, К и Ч изображают элементы первого множества (Белова, Краснова и Чернова), а черные кружочки б, к и ч – элементы второго множества – белое, красное и чёрное. Условимся соединять эти кружочки тонкой линией, если между ними нет соответствия. Если же соответствие между кружочками установлено правильно, то будем соединять их жирной линией. | Решение. Здесь мы имеем два равночисленных множества: множество фамилий и множество цветов платьев. Между этими множествами надо установить взаимно-однозначное соответствие. Для этого построим граф. Пусть белые кружочки Б, К и Ч изображают элементы первого множества (Белова, Краснова и Чернова), а черные кружочки б, к и ч – элементы второго множества – белое, красное и чёрное. Условимся соединять эти кружочки тонкой линией, если между ними нет соответствия. Если же соответствие между кружочками установлено правильно, то будем соединять их жирной линией. | ||
| − | + | [[Изображение:Рис_3.JPG]] | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
Следовательно, Белова одета в чёрное платье, Чернова одета в красное платье и Краснова – в белое платье. | Следовательно, Белова одета в чёрное платье, Чернова одета в красное платье и Краснова – в белое платье. | ||
| − | |||
| − | |||
2. Затем, можно предложить учащимся решить две задачи самостоятельно. Первые пятеро учащихся правильно решившие задачу получают оценку. Первые двое показывают решение на доске соответственно 1 и 2 задачи. | 2. Затем, можно предложить учащимся решить две задачи самостоятельно. Первые пятеро учащихся правильно решившие задачу получают оценку. Первые двое показывают решение на доске соответственно 1 и 2 задачи. | ||
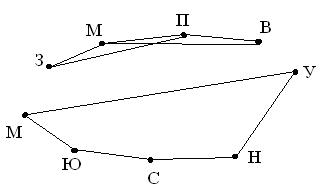
Задача 1. Между 9 планетами Солнечной системы введено космическое сообщение. Ракеты летают по следующим маршрутам: Земля–Меркурий, Плутон–Венера, Земля–Плутон, Плутон–Меркурий, Меркурий–Венера, Уран–Нептун, Нептун–Сатурн, Сатурн–Юпитер, Юпитер–Марс и Марс–Уран. Можно ли добраться с Земли до Марса? | Задача 1. Между 9 планетами Солнечной системы введено космическое сообщение. Ракеты летают по следующим маршрутам: Земля–Меркурий, Плутон–Венера, Земля–Плутон, Плутон–Меркурий, Меркурий–Венера, Уран–Нептун, Нептун–Сатурн, Сатурн–Юпитер, Юпитер–Марс и Марс–Уран. Можно ли добраться с Земли до Марса? | ||
Решение. Нарисуем граф, где вершины – это планеты, а ребра – это маршруты. | Решение. Нарисуем граф, где вершины – это планеты, а ребра – это маршруты. | ||
| − | + | ||
| + | [[Изображение:Рис_4.JPG]] | ||
| + | |||
Теперь видно, что долететь от Земли до Марса нельзя. | Теперь видно, что долететь от Земли до Марса нельзя. | ||
Задача 2. Петя, Гена, Дима и Вова занимаются в детской спортивной школе в разных секциях: гимнастической, баскетбольной, волейбольной и легкой атлетики. Петя, Дима и волейболист учатся в одном классе. Петя и Гена на тренировки ходят пешком вместе, а гимнаст ездит на автобусе. Легкоатлет не знаком ни с баскетболистом, ни с волейболистом. Кто из мальчиков в какой секции занимается? | Задача 2. Петя, Гена, Дима и Вова занимаются в детской спортивной школе в разных секциях: гимнастической, баскетбольной, волейбольной и легкой атлетики. Петя, Дима и волейболист учатся в одном классе. Петя и Гена на тренировки ходят пешком вместе, а гимнаст ездит на автобусе. Легкоатлет не знаком ни с баскетболистом, ни с волейболистом. Кто из мальчиков в какой секции занимается? | ||
Решение. Петя – баскетболист, Гена – волейболист, Дима – гимнаст, а Вова – легкоатлет. | Решение. Петя – баскетболист, Гена – волейболист, Дима – гимнаст, а Вова – легкоатлет. | ||
| − | + | ||
| + | [[Изображение:Рис_5.JPG]] | ||
| + | |||
3. Для закрепления изученного материала можно решить устно № 1220 (а) ( стр. 210, учебник «Математика 6», автор Н.Я. Виленкин, М.: Мнемозина, 2005.) | 3. Для закрепления изученного материала можно решить устно № 1220 (а) ( стр. 210, учебник «Математика 6», автор Н.Я. Виленкин, М.: Мнемозина, 2005.) | ||
| + | |||
Ответ: Витя знаком с Серёжей и Колей, Серёжа знаком с Витей и с Пете, Петя знаком с Серёжей и с Максимом, Максим знаком с Пете и с Колей, Коля знаком с Петей и с Витей. | Ответ: Витя знаком с Серёжей и Колей, Серёжа знаком с Витей и с Пете, Петя знаком с Серёжей и с Максимом, Максим знаком с Пете и с Колей, Коля знаком с Петей и с Витей. | ||
| + | |||
4. Домашнее задание. № 1249, № 1303. (учебник «Математика 6», автор Н.Я. Виленкин, М.: Мнемозина, 2005) | 4. Домашнее задание. № 1249, № 1303. (учебник «Математика 6», автор Н.Я. Виленкин, М.: Мнемозина, 2005) | ||
| + | |||
№ 1249. Вера, Нина, Оля и Люба надели платья разных цветов (красное, синее, белое, голубое). На вопрос, кто из них в каком платье, три девочки ответили: 1) Оля – в синем. Люба – в голубом; 2) Оля – в красном. Нина – в синем; 3) Вера – в синем, Люба – в голубом. В каждом ответе только одна часть верна, а другая нет. Какого цвета платье надела каждая девочка? | № 1249. Вера, Нина, Оля и Люба надели платья разных цветов (красное, синее, белое, голубое). На вопрос, кто из них в каком платье, три девочки ответили: 1) Оля – в синем. Люба – в голубом; 2) Оля – в красном. Нина – в синем; 3) Вера – в синем, Люба – в голубом. В каждом ответе только одна часть верна, а другая нет. Какого цвета платье надела каждая девочка? | ||
| + | |||
№ 1303. Марина, Лариса, Жанна и катя умеют играть на разных инструментах ( пианино, виолончели, гитаре, скрипке), но только каждая на одном. Они же знают иностранные языки (английский, французский, немецкий. Испанский), но каждая только один. Известно: 1) девушка, которая играет на гитаре, говорит по-испански; 2) Лариса не играет ни на скрипке, ни на виолончели и на знает английского языка; 3) Марина не играет ни на скрипке, ни на виолончели и на знает ни немецкого, ни английского языка; 4) девушка, которая говорит по-немецки, не играет на виолончели; 5( Жанна знает французский язык, но не играет на скрипке. Кто на каком инструменте играет и какой иностранный язык знает? | № 1303. Марина, Лариса, Жанна и катя умеют играть на разных инструментах ( пианино, виолончели, гитаре, скрипке), но только каждая на одном. Они же знают иностранные языки (английский, французский, немецкий. Испанский), но каждая только один. Известно: 1) девушка, которая играет на гитаре, говорит по-испански; 2) Лариса не играет ни на скрипке, ни на виолончели и на знает английского языка; 3) Марина не играет ни на скрипке, ни на виолончели и на знает ни немецкого, ни английского языка; 4) девушка, которая говорит по-немецки, не играет на виолончели; 5( Жанна знает французский язык, но не играет на скрипке. Кто на каком инструменте играет и какой иностранный язык знает? | ||
Версия 19:41, 31 марта 2008
Тема урока: «Решение логических задач с помощью графов». Класса: 6. Цель: Ввести понятие «графа», научить решать логические задачи с помощью графа. Ход урока: 1. Изучение темы полезно начать с решения конкретной задачи: Несколько мальчиков встретились на вокзале, чтобы поехать за город в лес. При встрече все они поздоровались друг с другом за руку. Сколько мальчиков поехало за город, если всего было 10 рукопожатий? Будем решать эту задачу графически. Вначале отметим точки А и В и соединим их отрезком. Точками будем изображать мальчиков, а отрезок будет означать рукопожатие. Добавим еще одну точку С и соединим её с точками А и В. Всего получается три отрезка.
Графы помогают решать некоторые задачи. Разберем одну из них.
Встретились три подруги: Белова, Краснова и Чернова. На одной из них было надето черное платье, на другой – красное, а на третьей белое. Девочка в красном платье говорит Черновой: « Нам надо поменяться платьями, а то цвет наших платьев не соответствует нашим фамилиям». Кто из девочек в какое платье был одет?
Решение. Здесь мы имеем два равночисленных множества: множество фамилий и множество цветов платьев. Между этими множествами надо установить взаимно-однозначное соответствие. Для этого построим граф. Пусть белые кружочки Б, К и Ч изображают элементы первого множества (Белова, Краснова и Чернова), а черные кружочки б, к и ч – элементы второго множества – белое, красное и чёрное. Условимся соединять эти кружочки тонкой линией, если между ними нет соответствия. Если же соответствие между кружочками установлено правильно, то будем соединять их жирной линией.
Следовательно, Белова одета в чёрное платье, Чернова одета в красное платье и Краснова – в белое платье.
2. Затем, можно предложить учащимся решить две задачи самостоятельно. Первые пятеро учащихся правильно решившие задачу получают оценку. Первые двое показывают решение на доске соответственно 1 и 2 задачи. Задача 1. Между 9 планетами Солнечной системы введено космическое сообщение. Ракеты летают по следующим маршрутам: Земля–Меркурий, Плутон–Венера, Земля–Плутон, Плутон–Меркурий, Меркурий–Венера, Уран–Нептун, Нептун–Сатурн, Сатурн–Юпитер, Юпитер–Марс и Марс–Уран. Можно ли добраться с Земли до Марса? Решение. Нарисуем граф, где вершины – это планеты, а ребра – это маршруты.
Теперь видно, что долететь от Земли до Марса нельзя. Задача 2. Петя, Гена, Дима и Вова занимаются в детской спортивной школе в разных секциях: гимнастической, баскетбольной, волейбольной и легкой атлетики. Петя, Дима и волейболист учатся в одном классе. Петя и Гена на тренировки ходят пешком вместе, а гимнаст ездит на автобусе. Легкоатлет не знаком ни с баскетболистом, ни с волейболистом. Кто из мальчиков в какой секции занимается? Решение. Петя – баскетболист, Гена – волейболист, Дима – гимнаст, а Вова – легкоатлет.
3. Для закрепления изученного материала можно решить устно № 1220 (а) ( стр. 210, учебник «Математика 6», автор Н.Я. Виленкин, М.: Мнемозина, 2005.)
Ответ: Витя знаком с Серёжей и Колей, Серёжа знаком с Витей и с Пете, Петя знаком с Серёжей и с Максимом, Максим знаком с Пете и с Колей, Коля знаком с Петей и с Витей.
4. Домашнее задание. № 1249, № 1303. (учебник «Математика 6», автор Н.Я. Виленкин, М.: Мнемозина, 2005)
№ 1249. Вера, Нина, Оля и Люба надели платья разных цветов (красное, синее, белое, голубое). На вопрос, кто из них в каком платье, три девочки ответили: 1) Оля – в синем. Люба – в голубом; 2) Оля – в красном. Нина – в синем; 3) Вера – в синем, Люба – в голубом. В каждом ответе только одна часть верна, а другая нет. Какого цвета платье надела каждая девочка?
№ 1303. Марина, Лариса, Жанна и катя умеют играть на разных инструментах ( пианино, виолончели, гитаре, скрипке), но только каждая на одном. Они же знают иностранные языки (английский, французский, немецкий. Испанский), но каждая только один. Известно: 1) девушка, которая играет на гитаре, говорит по-испански; 2) Лариса не играет ни на скрипке, ни на виолончели и на знает английского языка; 3) Марина не играет ни на скрипке, ни на виолончели и на знает ни немецкого, ни английского языка; 4) девушка, которая говорит по-немецки, не играет на виолончели; 5( Жанна знает французский язык, но не играет на скрипке. Кто на каком инструменте играет и какой иностранный язык знает?