Шестидесятеричная система счисления
(→История) |
|||
| (не показаны 2 промежуточные версии 1 участника) | |||
| Строка 7: | Строка 7: | ||
Происхождение шестидесятеричной системы неясно. Возможно, она связана с двенадцатеричной системой счисления (60 = 5×12, где 5 — число пальцев на руке). Возможно, с тем, что окружность делится циркулем на шесть частей. Существует также гипотеза О. Нейгебауэра о том, что после аккадского завоевания шумерского государства там долгое время одновременно существовали две денежно-весовые единицы: шекель(сикль) и Мина(единица измерения), причём было установлено их соотношение 1 мина = 60 шекелей. Позднее это деление стало привычным и породило соответствующую систему записи любых чисел. | Происхождение шестидесятеричной системы неясно. Возможно, она связана с двенадцатеричной системой счисления (60 = 5×12, где 5 — число пальцев на руке). Возможно, с тем, что окружность делится циркулем на шесть частей. Существует также гипотеза О. Нейгебауэра о том, что после аккадского завоевания шумерского государства там долгое время одновременно существовали две денежно-весовые единицы: шекель(сикль) и Мина(единица измерения), причём было установлено их соотношение 1 мина = 60 шекелей. Позднее это деление стало привычным и породило соответствующую систему записи любых чисел. | ||
| − | + | Вавилонское государство также унаследовало шестидесятеричную систему и передало её, вместе с таблицами наблюдений за небом, греческим астрономам. В более позднее время шестидесятеричная система использовалась арабами, а также древними и средневековыми астрономами, в первую очередь, для представления дробей. Поэтому средневековые учёные часто называли шестидесятеричные дроби «астрономическими». | |
| − | В | + | В XIII веке влиятельный ректор Парижского университета Пётр Филомен выступил за повсеместное внедрение шестидесятеричной системы в Европе. В XV веке с аналогичным призывом выступил Иоганн Гмунден, профессор математики Венского университета. Обе инициативы остались без последствий. |
| − | Начиная с XVI века, | + | Начиная с XVI века, десятичные дроби в Европе полностью вытесняют шестидесятеричные. Сейчас остатки шестидесятеричной системы используются в измерении углов и времени. |
== Структура шестидесятеричного числа == | == Структура шестидесятеричного числа == | ||
| − | Первый шестидесятеричный знак после запятой называется ''[[минута]]'' (′), второй — ''[[секунда]]'' (″). Ранее использовались названия ''[[терция]]'' (‴) для третьего знака, ''[[кварта]]'' (<sup>''IV''</sup>) для четвёртого знака, ''[[квинта]]'' (<sup>''V''</sup>) для пятого знака | + | Первый шестидесятеричный знак после запятой называется ''[[минута]]'' (′), второй — ''[[секунда]]'' (″). Ранее использовались названия ''[[терция]]'' (‴) для третьего знака, ''[[кварта]]'' (<sup>''IV''</sup>) для четвёртого знака, ''[[квинта]]'' (<sup>''V''</sup>) для пятого знака. Название «минута» происходит от того же слова, что и «минимум» — обозначает «малая часть», а «секунда», «терция» и остальные являются порядковыми — «второе» деление на части, «третье» деление на части. Частей традиционно берётся по 60. |
== Примеры использования == | == Примеры использования == | ||
| − | * 1 | + | * 1 радиан ≈ 57°17′45″ = <math>57 + \frac{17}{60} +\frac{45}{60^2}</math> градусов. |
| − | * | + | * Николай Коперник в знаменитой работе «О вращениях небесных сфер» даёт значение сидерического года 365;15′24″10‴ дней, приблизительно 365,25671 дней. |
[[Категория:ТГУ]] | [[Категория:ТГУ]] | ||
Текущая версия на 11:52, 20 сентября 2011
Автор-составитель: Игошин Александр
Шестидесятери́чная систе́ма счисле́ния — Позиционная система счисления|позиционная система счисления по целочисленному основанию 60. Использовалась в древние времена на Ближнем Востоке.
История
Происхождение шестидесятеричной системы неясно. Возможно, она связана с двенадцатеричной системой счисления (60 = 5×12, где 5 — число пальцев на руке). Возможно, с тем, что окружность делится циркулем на шесть частей. Существует также гипотеза О. Нейгебауэра о том, что после аккадского завоевания шумерского государства там долгое время одновременно существовали две денежно-весовые единицы: шекель(сикль) и Мина(единица измерения), причём было установлено их соотношение 1 мина = 60 шекелей. Позднее это деление стало привычным и породило соответствующую систему записи любых чисел.
Вавилонское государство также унаследовало шестидесятеричную систему и передало её, вместе с таблицами наблюдений за небом, греческим астрономам. В более позднее время шестидесятеричная система использовалась арабами, а также древними и средневековыми астрономами, в первую очередь, для представления дробей. Поэтому средневековые учёные часто называли шестидесятеричные дроби «астрономическими».
В XIII веке влиятельный ректор Парижского университета Пётр Филомен выступил за повсеместное внедрение шестидесятеричной системы в Европе. В XV веке с аналогичным призывом выступил Иоганн Гмунден, профессор математики Венского университета. Обе инициативы остались без последствий.
Начиная с XVI века, десятичные дроби в Европе полностью вытесняют шестидесятеричные. Сейчас остатки шестидесятеричной системы используются в измерении углов и времени.
Структура шестидесятеричного числа
Первый шестидесятеричный знак после запятой называется минута (′), второй — секунда (″). Ранее использовались названия терция (‴) для третьего знака, кварта (IV) для четвёртого знака, квинта (V) для пятого знака. Название «минута» происходит от того же слова, что и «минимум» — обозначает «малая часть», а «секунда», «терция» и остальные являются порядковыми — «второе» деление на части, «третье» деление на части. Частей традиционно берётся по 60.
Примеры использования
- 1 радиан ≈ 57°17′45″ =
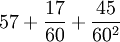градусов.
- Николай Коперник в знаменитой работе «О вращениях небесных сфер» даёт значение сидерического года 365;15′24″10‴ дней, приблизительно 365,25671 дней.
