Семинар ДООМ Применение графов при решении задач

Версия 18:36, 9 апреля 2008

Тихомирова Лариса Николаевна 111

Уважаемые коллеги, вашему вниманию предлагается план урока, который в рамках обучающего тура проводили участники команды «Лемниската» в 7 классе.

Цель урока:

• познакомить учащихся с термином «граф»

• ввести некоторые понятия теории графов

• показать применение теории графов на примерах решения некоторых задач

Ход урока.

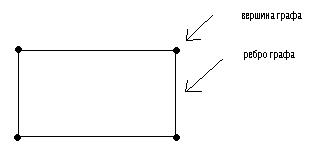
I. Ребята, кто-нибудь из вас слышал о графах в математическом смысле этого слова? Что же такое графы? Графы – это схемы, состоящие из точек (вершин графа) и соединяющих эти точки отрезков прямых или кривых (ребра графа).

Графы находят практическое применение в нашей жизни. Примеры графов: схема метро, где ребра – пути, соединяющие станции, а вершины – станции.

II. Для того чтобы научиться строить графы, решим следующую задачу.

Задача.

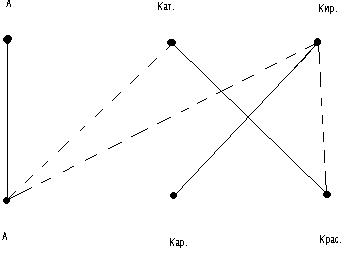
Известно, что у каждой из трех девочек фамилия начинается с той же буквы, что и имя. У Ани фамилия Анисимова. У Кати фамилия не Карева, а у Киры – не Краснова. Какая фамилия у каждой из девочек?

Решение.

По условию задачи составим граф, у которого вершины – имена и фамилии девочек. Сплошная линия будет обозначать, что девочке соответствует данная фамилия, а пунктирная – что не соответствует. Из условия задачи видно, что у Ани фамилия Анисимова (соединяем сплошной линией две соответствующие точки). Из этого следует, что у Кати и у Киры фамилия не Анисимова. Так как Катя – не Анисимова и не Карева, значит она Краснова. Остается, что у Киры фамилия Карева.

Задача.

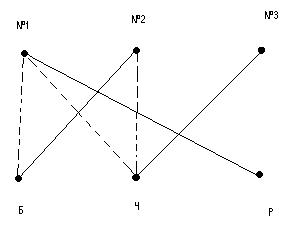
В квартирах №1, №2, №3 живут три котенка: белый, черный, рыжий. В квартире №1, №2 живут не черные котята. Белый котенок живет не в квартире №1. В какой квартире какой котенок живет?

Решение.

По условию задачи составим граф, из которого следует решение задачи.

III. Чтобы решать более сложные задачи, углубимся еще немного в теорию. Введем понятие степени вершины графа. Из каждой вершины графа выходит разное количество отрезков (прямолинейных и криволинейных), длины отрезков произвольны. Степень вершины – количество ребер графа, исходящих из этой вершины. Вершина называется нечетной – если степень этой вершины нечетная, четной – если степень этой вершины четная.

Сформулируем некоторые закономерности, присущие определенным графам.

1. Нельзя построить граф с нечетным количеством нечетных вершин.

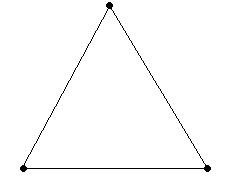
2. Если все вершины графа четные, то можно, не отрывая карандаш от бумаги и проводя по каждому ребру один раз, начертить этот граф. Закончить можно в той же вершине, с которой вы начали.

Пример.

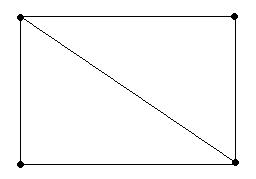
3. Граф, у которого две нечетные вершины, можно начертить одним росчерком.

Пример.

Ребятам предлагается нарисовать одним росчерком следующий граф и обосновать построение.

Задача о кенигсбергских мостах.

К XVIII веку через реку, на которой стоял город Кенигсберг, было построено семь мостов, которые связывали с берегами и друг другом два острова, расположенные в пределах города. На рисунке даны четыре моста. Дорисуйте еще три моста так, чтобы можно было пройти по каждому мосту один раз и вернуться к тому месту, откуда начался маршрут.

Решение.

Один мост между островами и еще два между каждым из островов и одним берегом.

В итоге хотелось выразить надежду, что прикоснувшись к «тайнам графов», вы ребята еще не раз с большим удовольствием будете решать задачи с применением изученной вами теории.