Семинар ДООМ Нарисуй фигуру
(Новая: Автор: Волкова Ольга Владимировна<br> ID_113<br><br> '''''Цель занятия:''''' развитие пространственного, логическ...) |
Nika (обсуждение | вклад) |
||
| (не показана 1 промежуточная версия 1 участника) | |||
| Строка 8: | Строка 8: | ||
''Вопрос:'' объясните, почему он смог нарисовать одним росчерком пера? <br> | ''Вопрос:'' объясните, почему он смог нарисовать одним росчерком пера? <br> | ||
В данном случае на рисунке точки четного порядка, а следовательно, вычертить такую фигуру одним росчерком без повторения тех же линий всегда можно. <br> | В данном случае на рисунке точки четного порядка, а следовательно, вычертить такую фигуру одним росчерком без повторения тех же линий всегда можно. <br> | ||
| − | Всегда можно также вычертить одним росчерком и такую фигуру, где, помимо точек четного порядка, есть и две точки (но не более) нечетного порядка. Весьма красивый ,и замысловатый образчик такой фигуры, заклю¬чающий в себе две нечетные точки А и Z, показан на рис. 2. С какой-нибудь из этих точек и надо | + | Всегда можно также вычертить одним росчерком и такую фигуру, где, помимо точек четного порядка, есть и две точки (но не более) нечетного порядка. Весьма красивый ,и замысловатый образчик такой фигуры, заклю¬чающий в себе две нечетные точки А и Z, показан на рис. 2. С какой-нибудь из этих точек и надо начинать непрерывное вычерчивание фигуры.<br> |
''Вопрос:'' можно ли вычертить одним росчерком фигуры на рис. 3 и 4?<br> | ''Вопрос:'' можно ли вычертить одним росчерком фигуры на рис. 3 и 4?<br> | ||
''Ответ:'' нет, при всей их видимой простоте, так как в первой восемь, а во второй — двенадцать точек нечетного порядка. Первая может быть вычерчена не менее как четырехкратной, т. е. состоящей из четырех непрерывных кусков, а вторая — не менее как шестикратной линией. | ''Ответ:'' нет, при всей их видимой простоте, так как в первой восемь, а во второй — двенадцать точек нечетного порядка. Первая может быть вычерчена не менее как четырехкратной, т. е. состоящей из четырех непрерывных кусков, а вторая — не менее как шестикратной линией. | ||
Если взять шахматную доску с 64 клетками, то в ней — 28 точек нечетного порядка, и, чтобы вычертить ее, надо чертить 14-кратную линию. С другой стороны, если взять треугольник, поделить каждую из его сторон на 12 (или сколько угодно) равных частей и провести из точек деления линии, параллельные другим сторонам, то полученная сетчатая фигура может быть вычерчена одним непрерывным движением без повторений. Таких примеров можно подобрать сколько угодно.<br> | Если взять шахматную доску с 64 клетками, то в ней — 28 точек нечетного порядка, и, чтобы вычертить ее, надо чертить 14-кратную линию. С другой стороны, если взять треугольник, поделить каждую из его сторон на 12 (или сколько угодно) равных частей и провести из точек деления линии, параллельные другим сторонам, то полученная сетчатая фигура может быть вычерчена одним непрерывным движением без повторений. Таких примеров можно подобрать сколько угодно.<br> | ||
<br> | <br> | ||
| + | <table align-right border=1> | ||
| + | <tr> <td> [[Изображение:gr_sem_1.jpg]]</td> <td> [[Изображение:gr_sem_2.jpg]]</td> <td> [[Изображение:gr_sem_3.jpg]]</td> <td> [[Изображение:gr_sem_4.jpg]]</td></tr> | ||
| + | <tr> <td> Рисунок 1</td> <td> Рисунок 2</td> <td> Рисунок 3</td> <td> Рисунок 4</td> | ||
| + | </table> | ||
'''Истории из Анголы.'''<br> | '''Истории из Анголы.'''<br> | ||
''''«Змея и птичье гнездо»''''<br> | ''''«Змея и птичье гнездо»''''<br> | ||
| Строка 33: | Строка 37: | ||
Нарисуйте четыре или пять птичек кумби в полете. <br> | Нарисуйте четыре или пять птичек кумби в полете. <br> | ||
Придумайте свою собственную лусону и рассказ к ней. Запишите свой рассказ и нарисуйте «сеть». <br> | Придумайте свою собственную лусону и рассказ к ней. Запишите свой рассказ и нарисуйте «сеть». <br> | ||
| + | <table align-right border=1> | ||
| + | <tr> <td> [[Изображение:gr_sem_5.jpg]]</td> <td> [[Изображение:gr_sem_6.jpg]]</td> <td> [[Изображение:gr_sem_7.jpg]]</td> <td> [[Изображение:gr_sem_8.jpg]]</td></tr> | ||
| + | <tr> <td> Рисунок 5</td> <td> Рисунок 6</td> <td> Рисунок 7</td> <td> Рисунок 8</td> | ||
| + | </table> | ||
''Примечание.'' Творческий проект можно потом создать из таких рассказов с иллюстрациями в виде их лусон.<br> | ''Примечание.'' Творческий проект можно потом создать из таких рассказов с иллюстрациями в виде их лусон.<br> | ||
'''''КАК НАЧИНАЛСЯ МИР (ЛЕГЕНДА)'''''<br> Лусоны в большинстве своем намного больше и сложнее, чем те, что были представлены до сих пор. Вот история, которую рассказывают в народе чокве, изображая при этом прекрасную лусону.<br> | '''''КАК НАЧИНАЛСЯ МИР (ЛЕГЕНДА)'''''<br> Лусоны в большинстве своем намного больше и сложнее, чем те, что были представлены до сих пор. Вот история, которую рассказывают в народе чокве, изображая при этом прекрасную лусону.<br> | ||
| Строка 56: | Строка 64: | ||
Раскрасьте рисунок, создав красивый узор.<br> | Раскрасьте рисунок, создав красивый узор.<br> | ||
Начертите большую сеть на листе ватмана, а потом наклейте поверх линий нитку другого цвета. Вы должны суметь пройти по всей сети, не разрывая нитку.<br> | Начертите большую сеть на листе ватмана, а потом наклейте поверх линий нитку другого цвета. Вы должны суметь пройти по всей сети, не разрывая нитку.<br> | ||
| + | <table align-right border=1> | ||
| + | <tr> <td> [[Изображение:gr_sem_9.jpg]]</td> <td> [[Изображение:gr_sem_10.jpg]]</td> <td> [[Изображение:gr_sem_11.jpg]]</td> <td> [[Изображение:gr_sem_12.jpg]]</td></tr> | ||
| + | <tr> <td> Рисунок 9</td> <td> Рисунок 10</td> <td> Рисунок 11</td> <td> Рисунок 12</td> | ||
| + | </table> | ||
''Домашние задания.'' <br>Для упражнения предлагается учащимся заняться во время досуга вычерчиванием с одного росчерка фигур, приведенных на рис. 13<br><br> | ''Домашние задания.'' <br>Для упражнения предлагается учащимся заняться во время досуга вычерчиванием с одного росчерка фигур, приведенных на рис. 13<br><br> | ||
| − | + | [[Изображение:gr_sem_13.jpg]]<br>Рисунок 13<br> | |
''Список использованной литературы:''<br> | ''Список использованной литературы:''<br> | ||
1. К.Заславски. Занимательная математика. Лучшие игры и задачи со всего мира. Мн: Попурри. 2005<br> | 1. К.Заславски. Занимательная математика. Лучшие игры и задачи со всего мира. Мн: Попурри. 2005<br> | ||
2. Е.И.Игнатьев. В царстве смекалки. М: Наука. 1978<br> | 2. Е.И.Игнатьев. В царстве смекалки. М: Наука. 1978<br> | ||
| − | [[Категория: | + | [[Категория:Архив проекта ДООМ 2007-2008 (2 цикл)]] |
Текущая версия на 09:06, 22 сентября 2008
Автор: Волкова Ольга Владимировна
ID_113
Цель занятия: развитие пространственного, логического мышления
Оборудование и наглядные материалы: карточки с рисунками, прозрачная бумага, карандаш.
Продолжительность: 3- 4 занятия
Аудитория: 5, 6 класс
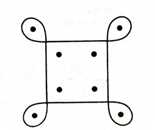
Говорят, что Магомет вместо подписи (он был неграмотен) описывал одним росчерком состоящий из двух рогов Луны знак, представленный на рис. 1.
Вопрос: объясните, почему он смог нарисовать одним росчерком пера?
В данном случае на рисунке точки четного порядка, а следовательно, вычертить такую фигуру одним росчерком без повторения тех же линий всегда можно.
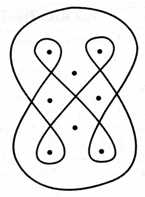
Всегда можно также вычертить одним росчерком и такую фигуру, где, помимо точек четного порядка, есть и две точки (но не более) нечетного порядка. Весьма красивый ,и замысловатый образчик такой фигуры, заклю¬чающий в себе две нечетные точки А и Z, показан на рис. 2. С какой-нибудь из этих точек и надо начинать непрерывное вычерчивание фигуры.
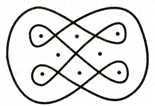
Вопрос: можно ли вычертить одним росчерком фигуры на рис. 3 и 4?
Ответ: нет, при всей их видимой простоте, так как в первой восемь, а во второй — двенадцать точек нечетного порядка. Первая может быть вычерчена не менее как четырехкратной, т. е. состоящей из четырех непрерывных кусков, а вторая — не менее как шестикратной линией.
Если взять шахматную доску с 64 клетками, то в ней — 28 точек нечетного порядка, и, чтобы вычертить ее, надо чертить 14-кратную линию. С другой стороны, если взять треугольник, поделить каждую из его сторон на 12 (или сколько угодно) равных частей и провести из точек деления линии, параллельные другим сторонам, то полученная сетчатая фигура может быть вычерчена одним непрерывным движением без повторений. Таких примеров можно подобрать сколько угодно.
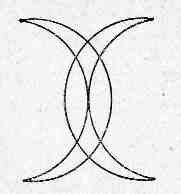 | 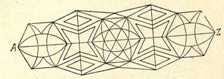 | 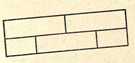 | 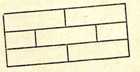 |
| Рисунок 1 | Рисунок 2 | Рисунок 3 | Рисунок 4 |
Истории из Анголы.
'«Змея и птичье гнездо»'
Ласточка построила гнездо между четырех ветвей. Услышав писк птенцов, змея решила посмотреть на них. Она подползла к гнезду и обвилась вокруг первой ветви. Затем змея поползла дальше и обвилась вокруг второй ветви, потом вокруг третьей и вокруг четвертой, и вернулась к начальной точке (рис.5). Так она продолжала извиваться среди четырех ветвей несколько дней. Однажды она не услышала щебета птиц и решила посмотреть, что же случилось. Когда змея, наконец, заглянула в гнездо, оно оказалось пустым.
Вопросы: Зачем змее понадобилось птичье гнездо? Почему она не смогла в него попасть? Куда делись птенцы, когда змея, наконец, добралась до гнезда?
Задания: Нанесите на лист бумаги показанную схему точек. Потом нарисуйте путь змеи среди четырех ветвей. Не отрывайте карандаш от бумаги и никакую линию не проходите дважды. Попрактиковавшись, расскажите эту историю другу или братику с сестричкой, одновременно рисуя лусону.
«Рассказчики народа чокве»
Народ чокве живет в северо-западной части африканской страны Анголы. Когда там еще не было ни радио, ни телевидения, ни школ, дети узнавали о жизни других людей из рассказов стариков. В свободное время они собирались вокруг костра или в тени большого дерева, слушая истории о людях и животных. По ходу истории рассказчик рисовал на земле своего рода иллюстрации, узоры, называемые лусонами. Мы называем такие узоры «сетями». Сеть — это система линий, соединяющих точки. Вспомните телевизионные сети, телефонные сети, сети городских улиц, Интернет. Сети окружают нас со всех сторон!
Сначала рассказчик наносил на песке систему точек, а потом по ходу повествования обводил эти точки непрерывной линией, ни разу не отрывая палец от земли и ни на секунду не прерывая свой рассказ. Так и получалась лусона.
ЗАГАДКА
Лусона, изображенная на рис. 6,— это загадка. Рассказчик, начертивший эту фигуру, сначала создал схему точек, которые потом обвел непрерывной линией.
Можете догадаться, что это такое? Вот несколько подсказок. Этой штукой можно передавать сообщения; ею можно отбивать ритм, чтобы можно было танцевать; сверху и снизу она обтянута кожей.
ИСТОРИЯ ПРО ЖИВОТНЫХ
Другой старик рассказывал детям про антилопу, убегавшую от леопарда. Убегая, она оставляла на земле следы. На рис. 7 изображен отпечаток одного ее копыта.
Вопросы: Сравните две лусоны. Насколько они похожи? Чем отличаются?
Ответ на загадку — двусторонний барабан. Он обтянут кожей сверху и снизу. Похож ли приведенный рисунок на барабан? А второй рисунок похож на отпечаток копыта?
Задание. Положите на изображенную на листке бумаги лусону (рис. 6, 7) полупрозрачный лист бумаги. Карандашом скопируйте узор. Старайтесь не отрывать карандаш от бумаги и не проводить линии дважды. Пересекать линии можно. Попрактикуйтесь, пока это не начнет у вас получаться легко.
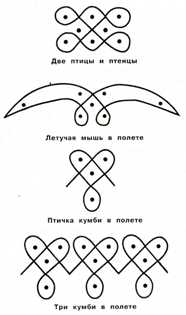
Если бы вы побывали в гостях у представителей народа чокве, вы бы увидели лусоны у них на стенах. Рисованием этих узоров с удовольствием занимаются мужчины, женщины и даже дети. На рисунке 8 показано несколько изображений, которые можно увидеть на стенах их домов.
Задания. Положите поверх лусоны лист тонкой бумаги, чтобы узор просвечивался. Обведите его карандашом. Повторите эти «сети» на отдельном листе, не отрывая карандаш от бумаги. Предварительно нанесите схему точек. Рисуйте карандашом, чтобы можно было стереть неудачные линии. В конце обведите получившийся рисунок фломастером. Придумайте подходящую историю, которую можно было бы рассказывать другу и при этом вычерчивать лусону.
Нарисуйте четыре или пять птичек кумби в полете.
Придумайте свою собственную лусону и рассказ к ней. Запишите свой рассказ и нарисуйте «сеть».
 |  |  |  |
| Рисунок 5 | Рисунок 6 | Рисунок 7 | Рисунок 8 |
Примечание. Творческий проект можно потом создать из таких рассказов с иллюстрациями в виде их лусон.
КАК НАЧИНАЛСЯ МИР (ЛЕГЕНДА)
Лусоны в большинстве своем намного больше и сложнее, чем те, что были представлены до сих пор. Вот история, которую рассказывают в народе чокве, изображая при этом прекрасную лусону.
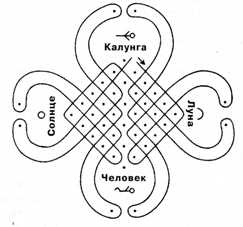
Когда-то Солнце решило засвидетельствовать свое почтение богу Калунге. Оно ходило, бродило, пока не нашло пути к нему. Когда Солнце предстало перед Калунгой, тот дал ему петуха и сказал: «Приходи ко мне утром».
Утром петух закричал, разбудил Солнце, и оно тут же оправилось к Калунге. А он и говорит: «Я услышал крик петуха, которого дал тебе на ужин. Можешь оставить его в живых, но тогда ты должен каждое утро возвращаться ко мне». Вот почему солнце каждое утро поднимается над землей.
Луна тоже посетила Калунгу и тоже получила петуха. Утром петух разбудил Луну, и она с ним под мышкой вернулась к Калунге. Тот сказал: «Я вижу, ты не съела петуха, которого я дал тебе вчера. Это хорошо. Ты должна возвращаться ко мне каждые двадцать восемь дней». Вот почему мы видим полную луну каждые двадцать восемь дней.
Человек тоже пришел к Калунге и тоже ушел с петухом. Но после такого долгого пути Человек очень про¬голодался и съел часть петуха на ужин. Наутро солнце было уже очень высоко, когда Человек проснулся. Он быстро доел петуха и поспешил к богу Калунге, который сказал ему с улыбкой: «Где же петух, которого я дал тебе вчера? Я что-то не слышал его крика сегодня утром».
Человек испугался. «Я был очень голоден и съел его»,— сказал он.
Тогда Калунга сказал: «Не бойся, но послушай, что я скажу. Ты знаешь, что Солнце и Луна тоже были у меня и получили по петуху. Но они не убили своих петухов. Поэтому они и сами никогда не умрут. Но ты убил своего петуха и потому должен умереть, как и он. Приходи ко мне после смерти».
И так продолжается до сих пор. Солнце и луна продолжают появляться на небе, как они появлялись в дни наших прадедов. А люди смертны (см. рис.9).
Задание. Пальцем отследите путь, проделанный Солнцем. Луной и Человеком. Стрелка подскажет вам, откуда начать. Можно ли сделать это, не отрывая пальца от бумаги? Нарисовать урок будет нелегко!
Многие лусоны еще даже сложнее показанной на рис.9. Люди, придумавшие эти узоры, были очень умны!
ДЕТСКИЕ «СЕТИ» ИЗ КОНГО
Много лет назад венгерский антрополог Эмиль Тордай некоторое время жил в гостях у народа куба в Конго. Его там поразила красота местных тканей и резьба по дереву (рис. 10). Народ этот живет в пойме реки Касаи, и многие семьи промышляют рыбной ловлей.
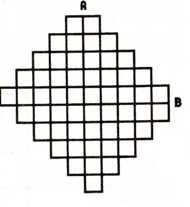
Однажды Тордай увидел детей, рисовавших на при¬брежном песке какие-то узоры. Они пригласили его посидеть рядом и предложили начертить два узора, не отрывая палец от песка и не проходя ни одну линию дважды. Узоры эти напоминали те сети, которыми их родители ловили рыбу. Один из таких узоров представлен на рис. 11.
Тордай писал в своей книге: «Меня попросили решить совершенно непосильную головоломку. Велика же была их радость, когда белому человеку это не удалось». Потом они показали ему, как это делается.
Задания. Давайте присмотримся к этой «сети» повниматель¬нее. В самом длинном горизонтальном ряду и в самом длинном вертикальном она содержит по десять клеток. Начнем построение таких сетей на более простом при¬мере, а потом перейдем к более сложным.
Взгляните на некоторые примеры сравнительно про¬стых сетей, показанные на рис. 12. В самом длинном ряду нижней сети всего две клетки. Средняя сеть имеет в самом длинном ряду три клетки, а верхняя — четыре.
Скопируйте самую маленькую сеть, представленную на рис. 12, не отрывая карандаш от бумаги и не проходя ни одной линии дважды. Пересекать линии можно. Есть ли какие-то особые точки, откуда следует начинать, или можно начать с любого места? Попробуйте начать в разных точках. Не стирайте свою работу, даже если не получается. Вам нужно выяснить, какие пути ведут к успеху, а какие нет.
Соблюдая те же правила, постройте сеть побольше, с тремя клетками в самом длинном ряду. Потом еще большую сеть — с четырьмя клетками. Рисунок получается наиболее аккуратным, если вести линию, не останавливаясь, пока она не изменит направление. Отметьте на каждой сети точку начала и точку конца. Что вы можете сказать об этих точках? Можете ли вы найти их с первой попытки?
Начертите сеть с пятью клетками в самом длин¬ном ряду. Продолжайте строить сети, с каждым разом увеличивая на единицу количество клеток в самом длинном ряду. Отмечайте точки начала и конца.
Нарисуйте сеть, которую рисовали дети народа куба на песке — с десятью клетками в самом длинном ряду. Не отрывайте карандаш от бумаги и не проходите линии дважды. Пересекать линии можно.
Раскрасьте рисунок, создав красивый узор.
Начертите большую сеть на листе ватмана, а потом наклейте поверх линий нитку другого цвета. Вы должны суметь пройти по всей сети, не разрывая нитку.
 |  |  |  |
| Рисунок 9 | Рисунок 10 | Рисунок 11 | Рисунок 12 |
Домашние задания.
Для упражнения предлагается учащимся заняться во время досуга вычерчиванием с одного росчерка фигур, приведенных на рис. 13
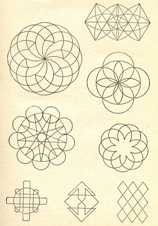
Рисунок 13
Список использованной литературы:
1. К.Заславски. Занимательная математика. Лучшие игры и задачи со всего мира. Мн: Попурри. 2005
2. Е.И.Игнатьев. В царстве смекалки. М: Наука. 1978
