Семинар ДООМ задачки
Nika (обсуждение | вклад) |
|||
| (не показаны 4 промежуточные версии 1 участника) | |||
| Строка 1: | Строка 1: | ||
| + | Сафарчева Ирина Ивановна ID_130 | ||
| + | |||
1.Король решил обойти все свои башни и закончить маршрут у башни с флажком. Как ему это сделать, не заходя в одно и то же место дважды? | 1.Король решил обойти все свои башни и закончить маршрут у башни с флажком. Как ему это сделать, не заходя в одно и то же место дважды? | ||
[[Изображение:Korol_.jpg]] | [[Изображение:Korol_.jpg]] | ||
| Строка 15: | Строка 17: | ||
8. Из Лидова в Кузьминки можно проехать на автобусе с пересадкой в Марьино или Сергеевке. Время движения автобуса между этими поселками указано на схеме: | 8. Из Лидова в Кузьминки можно проехать на автобусе с пересадкой в Марьино или Сергеевке. Время движения автобуса между этими поселками указано на схеме: | ||
| − | + | [[Изображение:Kuzminki_.jpg]] | |
Какой путь выгоднее, если известно, что в Марьино приходится ждать автобуса 5 мин, а в Сергеевке — 15 мин? | Какой путь выгоднее, если известно, что в Марьино приходится ждать автобуса 5 мин, а в Сергеевке — 15 мин? | ||
| Строка 23: | Строка 25: | ||
10. В семи кружках расставлены числа от 1 до 7 так, что сумма четырех чисел, расположенных в вершинах каждого четырехугольника, составляет 13. Расставь эти же числа так, чтобы сумма четырех чисел в вершине каждого четырехугольника была равна 14, 15, 16, 17. | 10. В семи кружках расставлены числа от 1 до 7 так, что сумма четырех чисел, расположенных в вершинах каждого четырехугольника, составляет 13. Расставь эти же числа так, чтобы сумма четырех чисел в вершине каждого четырехугольника была равна 14, 15, 16, 17. | ||
| + | [[Изображение:Kub.jpg]] | ||
Здравствуйте, уважаемые коллеги.Была очень удивлена тем фактом, что задачи такого уровня есть уже начиная с начальной школы. Привожу несколько из них, которые меня более всего заинтересовали. | Здравствуйте, уважаемые коллеги.Была очень удивлена тем фактом, что задачи такого уровня есть уже начиная с начальной школы. Привожу несколько из них, которые меня более всего заинтересовали. | ||
| + | |||
| + | [[Категория:Архив проекта ДООМ 2007-2008 (2 цикл)]] | ||
Текущая версия на 09:08, 22 сентября 2008
Сафарчева Ирина Ивановна ID_130
1.Король решил обойти все свои башни и закончить маршрут у башни с флажком. Как ему это сделать, не заходя в одно и то же место дважды?
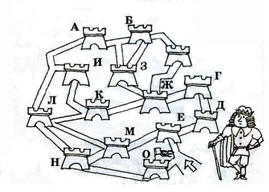
2.Саша, Сережа, Дима и Алеша получили за контрольную работу оценки: «5», «5», «4», «3». Саша получил отметку, более высокую, чем Дима, а Сережа получил такую же оценку как Алеша. Кто получил тройку?
3.Для Вани, Толи и Миши есть три порога: с рисом, капустой и яблоками. Миши не любит пирог с яблоками, и не ест с капустой. Ваня не любит пирог с капустой. Какие пироги они выберут?
4.К берегу реки подошли три людоеда. У каждого из них по одному слуге. В присутствии хозяина его слугу съедают другие людоеды. Всем им надо перебраться на другой берег в двухместной лодке. Как это сделать, чтобы никто никого не съел?
5.Слова в словарях расположены по следующим правилам: раньше пишут то слово, у которого первая из несовпадающих букв идет в алфавите раньше. расположи в словарном порядке слова: лист, лакомка, лад, луна, ласточка, ладонь, лето, ласка, ливень, лес, лось, лицо.
6.Нарисуй схему Волшебной страны, если известно, что Голубая, Фиолетовая и Розовая страны имеют общую границу с остальными четырьмя частями. Желтая страна и Изумрудный город не имеют между собой общей границы, причем Желтая страна окружена со всех сторон Великой пустыней, отделяющей Волшебную страну от остального мира.
7.Несколько калуш встретились на опушке. Каждая с каждой поздоровались за лапу. Сколько всего калуш, если было десять рукопожатий.
8. Из Лидова в Кузьминки можно проехать на автобусе с пересадкой в Марьино или Сергеевке. Время движения автобуса между этими поселками указано на схеме:
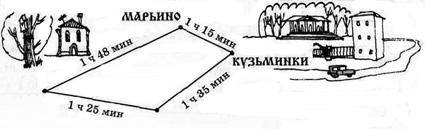
Какой путь выгоднее, если известно, что в Марьино приходится ждать автобуса 5 мин, а в Сергеевке — 15 мин?
9. В третьем классе учатся 25 учеников. Им было предложено заниматься в двух кружках: по математике и по "окружающему миру". В каждый записалось по 16 человек, причем 10 человек решили заниматься одновременно математикой и "окружающим миром". Получив результаты, ребята удивились: "Можно подумать, что у нас в классе не 25 учеников, а все 42!" Но один любитель математики сказал: "Вовсе нет! У нас есть несколько ребят, которые не хотят заниматься ни в одном из кружков. Я даже могу сказать, сколько их". Как он это узнал?
10. В семи кружках расставлены числа от 1 до 7 так, что сумма четырех чисел, расположенных в вершинах каждого четырехугольника, составляет 13. Расставь эти же числа так, чтобы сумма четырех чисел в вершине каждого четырехугольника была равна 14, 15, 16, 17.
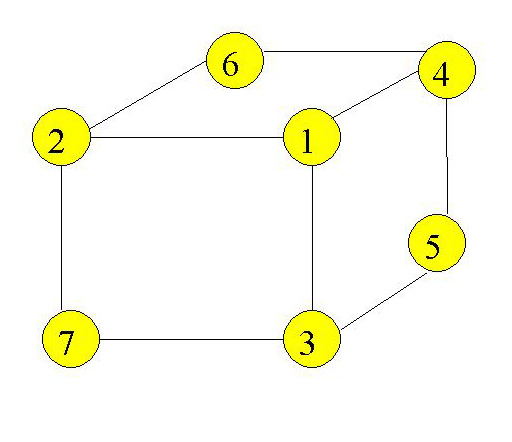
Здравствуйте, уважаемые коллеги.Была очень удивлена тем фактом, что задачи такого уровня есть уже начиная с начальной школы. Привожу несколько из них, которые меня более всего заинтересовали.
