Развертки цилиндра и конуса
(Отмена правки 390600, сделанной участником Gugiugghghj (обс.)) |
|||
| (не показаны 8 промежуточных версий 4 участников) | |||
| Строка 23: | Строка 23: | ||
Изображение: АВС6.JPG|a | Изображение: АВС6.JPG|a | ||
Изображение: АВС7.JPG|б | Изображение: АВС7.JPG|б | ||
| − | Изображение: АВС8.JPG | + | Изображение: АВС8.JPG|в |
</gallery> | </gallery> | ||
| Строка 30: | Строка 30: | ||
Поверхность усеченного конуса состоит двух кругов радиуса R1 , R2 и сегмента круга радиуса OA. Дуга AB=2пR. Изображение усеченного конуса и его разверток показаны на рисунках: | Поверхность усеченного конуса состоит двух кругов радиуса R1 , R2 и сегмента круга радиуса OA. Дуга AB=2пR. Изображение усеченного конуса и его разверток показаны на рисунках: | ||
| − | [[Изображение: АВС9. | + | [[Изображение: АВС9.JPG]] |
а) Когда угол прямой имеем четверть круга. Чтобы дуга AA1=2пR1, и дуга BB1=2пR надо чтобы А1О=4R1, В1О=4R2 | а) Когда угол прямой имеем четверть круга. Чтобы дуга AA1=2пR1, и дуга BB1=2пR надо чтобы А1О=4R1, В1О=4R2 | ||
| Строка 41: | Строка 41: | ||
Изображение: АВС2.jpg|a | Изображение: АВС2.jpg|a | ||
Изображение: АВС1.jpg|б | Изображение: АВС1.jpg|б | ||
| − | Изображение: АВС3.jpg | + | Изображение: АВС3.jpg|в |
</gallery> | </gallery> | ||
| + | |||
| + | [[Категория:Проект ДООМ 2009-2010]] | ||
Текущая версия на 15:18, 14 декабря 2013
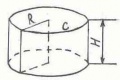
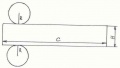
Развертка «Цилиндр»
Поверхность цилиндра состоит из двух равных кругов радиуса R и прямоугольника, ширина которого равна высоте цилиндра, длина вычисляется по формуле С=2пR , где п=3,14. Изображение цилиндра и его развертка на рисунках:
Изображение цилиндра
Развертка цилиндра
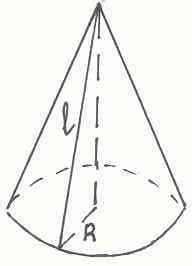
Развертка «Конус»
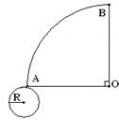
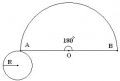
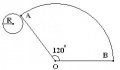
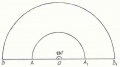
Поверхность конуса состоит круга радиуса R и сегмента круга радиуса OA. Дуга АВ=2пR. Изображение конуса и его разверток показаны на рисунках:
а) Когда угол прямой имеем четверть круга. Чтобы дуга АВ=2пR, надо чтобы АО=4R
б) Когда угол развернутый имеем половину круга. Чтобы дуга АВ=2пR, надо чтобы АО=2R
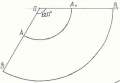
в) Когда угол 120 градусов имеем треть круга. Чтобы дуга AB=2пR, надо чтобы АО=3R
a
б
в
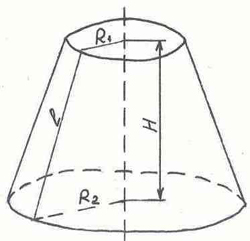
Развертка «Усеченный конус»
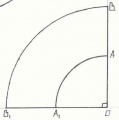
Поверхность усеченного конуса состоит двух кругов радиуса R1 , R2 и сегмента круга радиуса OA. Дуга AB=2пR. Изображение усеченного конуса и его разверток показаны на рисунках:
а) Когда угол прямой имеем четверть круга. Чтобы дуга AA1=2пR1, и дуга BB1=2пR надо чтобы А1О=4R1, В1О=4R2
б) Когда угол развернутый имеем половину круга. Чтобы дуга AA1=2пR1, и дуга BB1=2пR надо чтобы А1О=2R1, В1О=2R2
в) Когда угол 120 градусов имеем треть круга. Чтобы дуга AA1=2пR1, и дуга BB1=2пR надо чтобы А1О=3R1, В1О=3R2
a
б
в
