Комбинаторные задачи 6 класс
(→Презентация) |
|||
| (не показаны 2 промежуточные версии 2 участников) | |||
| Строка 5: | Строка 5: | ||
[[Участник:Астапова Александра|Астапова Александра Анатольевна]] | [[Участник:Астапова Александра|Астапова Александра Анатольевна]] | ||
| − | '''Место работы''': | + | '''Место работы''': МБУ "Школа № 32 г.о. Тольятти |
| − | [http://mou32.togliatty.rosshkola.ru сайт | + | [http://mou32.togliatty.rosshkola.ru сайт МБУ "Школа №32"] |
== Название урока == | == Название урока == | ||
| Строка 161: | Строка 161: | ||
==Презентация == | ==Презентация == | ||
| − | [https://docs.google.com/present/ | + | [https://docs.google.com/present/view?id=dhhc43z9_317g773d8f5&revision=_latest&start=0&theme=blank&cwj=true|| Презентация к уроку "Решение комбинаторных задач] |
==Фото отчет == | ==Фото отчет == | ||
| Строка 188: | Строка 188: | ||
3. Алгебра. Элементы статистики и теории вероятностей. Учебное пособие под редакцией С.А.Теляковского. Москва: «Просвещение», 2005. | 3. Алгебра. Элементы статистики и теории вероятностей. Учебное пособие под редакцией С.А.Теляковского. Москва: «Просвещение», 2005. | ||
| − | [[Категория: | + | [[Категория:Предметы научно-технического цикла]] |
Текущая версия на 20:12, 1 мая 2017
Содержание |
Автор урока
Астапова Александра Анатольевна
Место работы: МБУ "Школа № 32 г.о. Тольятти
Название урока
Решение комбинаторных задач
Предмет, класс
математика, 6 класс
Цели урока
Ввести понятие комбинаторики; сформировать представление о комбинаторных задачах; научить строить дерево возможных вариантов; повторить сложение и вычитание дробей с разными знаменателями; развитие логического мышления.
Ход урока
1. Организационный момент
Учитель объясняет тему урока и цель.
2. Новый материал объяснить в ходе решения трех задач.
Презентация «Комбинаторика» (Приложение 1).
Задача№1
Государственные флаги многих стран состоят из горизонтальных или вертикальных полос разных цветов. Сколько существует различных флагов, состоящих из двух горизонтальных полос одинаковой ширины и разного цвета – белого, красного и синего?
Решение:
Пусть верхняя полоса флага – белая (Б). Тогда нижняя полоса может быть красной (К) или синей (С). Получили две комбинации – два варианта флага. Если верхняя полоса флага – красная, то нижняя может быть белой или синей. Получим ещё два варианта флага. Пусть, наконец, верхняя полоса – синяя, тогда нижняя может быть белой или красной. Это ещё два варианта флага. Всего получили 3 • 2 = 6 комбинаций – шесть вариантов флагов.
Задачи, решая которые приходится составлять различные комбинации из конечного числа элементов и подсчитывать число комбинаций, получили названиекомбинаторных .
Раздел математики, в котором рассматривают такие задачи, называют комбинаторикой. Комбинаторика (от латинского combinare) означает “соединять, сочетать”.
Задача 2
Сколько трехзначных чисел можно составить из цифр 1, 3, 5, 7? Используя в записи числа каждую из них не более одного раза?
Решение:
Чтобы ответить на этот вопрос, выпишем все такие числа. Пусть на первом месте стоит цифра 1. На втором месте может быть записана любая из цифр 3, 5, 7. Запишем, например, на втором месте цифру 3. Тогда в качестве третьей цифры можно взять 5 или 7. Получим два числа 135 и 137. Если на втором месте записать цифру 5, то в качестве третьей цифры можно взять цифру 3или 7. В этом случае получим числа 153 и 157. Если же, наконец, на втором месте записать цифру 7, то получим числа 173 и 175. Итак, мы составили все числа, которые начинаются с цифры 1. Таких чисел шесть: 135, 137, 153, 157, 173, 175. Аналогичным способом можно составить числа, которые начинаются с цифры 2,с цифры 5, с цифры 7.
Полученные результаты запишем в четыре строки, в каждой из которых шесть чисел:
135, 137, 153, 157, 173, 175, 315, 317, 351, 357, 371, 375, 513, 517, 531, 537, 571, 573, 713, 715, 731, 735, 751, 753,
Таким образом, из цифр 1, 3, 5, 7 (без повторения цифр) можно составить 24 трехзначных числа.
Проведенный перебор вариантов проиллюстрирован на так называемом дереве возможных вариантов. Ответ на вопрос, поставленный в задаче, можно получить, не выписывая сами числа. Рассуждая так. Первую цифру можно выбрать 4 способами. Так как после выбора первой цифры останутся 3, то вторую цифру можно выбрать уже 3 способами. Наконец, третью цифру можно выбрать (из оставшихся двух) 2 способами. Следовательно, общее число искомых трехзначных чисел равно произведению 4 • 3 • 2, т.е. 24. Ответ на поставленный в задаче вопрос мы нашли, используя комбинаторное правило умножения. Пусть имеется n элементов и требуется выбрать один за другим некоторые k элементов. Если первый элемент можно выбрать n1 способами, после чего второй элемент можно выбрать из оставшихся элементов n2 способами, затем третий элемент n3 способами и т. д., то число способов, которыми могут быть выбраны все k элементов, равно произведению n1 • n2 • n3 • …• nk.
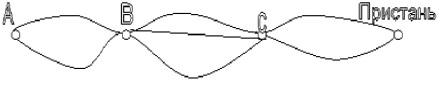
Задача 3 Из города А в город В ведут две дороги, из города В в город С – три дороги, из города С до пристани – две дороги. Туристы хотят проехать из города А через города В и С к пристани. Сколькими способами они могут выбрать маршрут?
Решение: Путь из А в В туристы могут выбрать двумя способами. Далее в каждом случае они могут проехать из В в С тремя способами. Значит, имеются 2 • 3 вариантов маршрута из А в С. Так как из города С на пристань можно попасть двумя способами, то всего существует 2 • 3 • 2, т.е. 12 способов выбора туристами маршрута из города А к пристани. 3. Тренировочные упражнения (Задания в виде презентации «Комбинаторика» или карточек.).
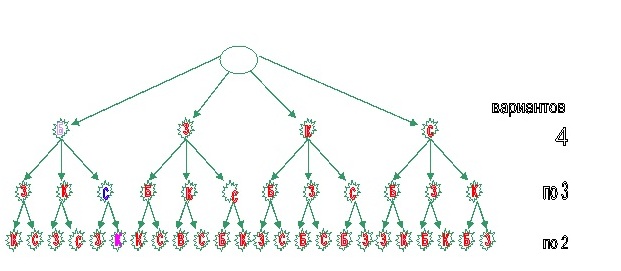
Задание 1 Сколько существует флагов составленных из трёх горизонтальных полос одинаковой ширины и различных цветов –белого, зелёного, красного и синего? Есть ли среди них флаг Российской Федерации. (Ребята самостоятельно решают задачу. Решив задачу, проверяют ответ, вставив пропущенные числа. Ответ в задаче и в примере одинаковый.)
Решение: Таким образом, 4 • 3 • 2 = 24 флага. Ответ: 24 флага, да.
Задание 2
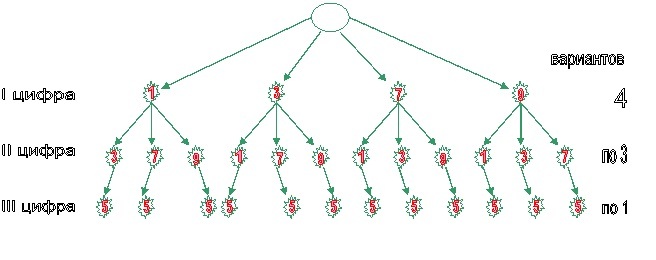
Сколько различных трехзначных чисел (без повторения цифр) можно составить из нечётных цифр, которые являются кратными 5. Прежде чем решать эту задачу, давайте повторим, какие цифры нечётные? Какие числа являются кратными 5.
Решение: Нечётные цифры: 1, 3, 5, 7, 9. В данном случае, чтобы число было кратным 5, оно должно оканчиваться на 5. Составим дерево возможных вариантов.
Таким образом, 4 • 3 • 1 = 12 чисел.
Задание 3 В школьной столовой предлагают 2 первых блюда: борщ, лапша – и 4 вторых блюда: пельмени, котлеты, гуляш, рыба. Сколько обедов из двух блюд может заказать посетитель. Перечислите их.
Решение: 1 блюдо: Б Л 2 возможности 2 блюдо: П К Г Р П К Г Р по 4 Таким образом, 2 • 4 = 8 различных обедов: Борщ, пельмени; Лапша, пельмени; Борщ, котлеты; Лапша, котлеты; Борщ, гуляш; Лапша, гуляш; Борщ, рыба; Лапша, рыба.
Задание 4 Учащиеся 6 класса решили обменяться фотографиями. Сколько фотографий для этого потребуется, если в классе 11 учащихся. Решение: 11 человек по 10 фотографий. 11 • 10 = 110 (фотографий). Ответ: 110 фотографий.
Задание 5 Из села Ташла в село Пискалы ведут три дороги, а из села Пискалы в город Тольятти – четыре дороги. Сколькими способами можно попасть из села Тащла в город Тольятти через село Пискалы?
Решение: 3 дороги по 4 варианта, т.е. 3 • 4 = 12 (способов). Ответ: 12 способов.
Задание 6 В кафе имеются четыре первых блюда, пять вторых и два третьих. Сколькими способами посетители кафе могут выбрать обед, состоящий из первого, второго и третьего блюд?
Решение: 4 • 5 • 2 = 40 (способов) Ответ: 40 способов.
Итог урока
– Какие задачи называются комбинаторными?
– Что означает слово «комбинаторика»?
– Как формулируется комбинаторное правило умножения?–
Домашние задание
Придумать и решить три комбинаторных задачи
Презентация
Презентация к уроку "Решение комбинаторных задач
Фото отчет
Материалы по формирующему и итоговому оцениванию
Итоговое оценивание с помощью смайликов
Материалы по сопровождению урока
Литература:
1. Учебник «Математика 6» Н.Я.Виленкин, В.И.Жохов и др. Москва: «Мнемозина», 2006.
2. Учебник И.И. Зубарева, А.Г. Мордкович Москва: «Мнемозина», 2005
3. Алгебра. Элементы статистики и теории вероятностей. Учебное пособие под редакцией С.А.Теляковского. Москва: «Просвещение», 2005.