Семинар ДООМ Использование графиков при решении текстовых задач
(Новая: Использование графиков равномерного движения при решении текстовых задач по алгебре Обычно при реш...) |
|||
| (не показаны 8 промежуточных версий 1 участника) | |||
| Строка 1: | Строка 1: | ||
| − | Использование графиков равномерного движения при решении текстовых задач по алгебре | + | '''Использование графиков равномерного движения при решении текстовых задач по алгебре.''' |
| − | Обычно при решении текстовых задач на движение для наглядности пройденное | + | |
| − | Отметим, что при решении задач на | + | Обычно при решении текстовых задач на движение для наглядности пройденное расстояние изображают отрезком, однако это не всегда упрощает решение. Указанный недостаток можно устранить, применяя графическое представление движения, известное учащимся из курса физики. |
| − | + | Отметим, что при решении задач на равномерное движение полезны соотношения: | |
| + | |||
| + | S1 : S2 =t1 : t2 – если скорости равны; | ||
| + | |||
V1 : V2 =t1 : t2 – если равны пройденные расстояния; | V1 : V2 =t1 : t2 – если равны пройденные расстояния; | ||
| + | |||
S1 : S2 = V1 : V2 – если равны промежутки времени; | S1 : S2 = V1 : V2 – если равны промежутки времени; | ||
| + | |||
Кроме того, известно, что тангенс угла наклона прямой x=х0 +Vt к оси Ot численно равен скорости тела. | Кроме того, известно, что тангенс угла наклона прямой x=х0 +Vt к оси Ot численно равен скорости тела. | ||
| − | Рассмотрим решение нескольких задач, | + | Рассмотрим решение нескольких задач, используя график равномерного движения. |
| − | Задача 1 Из двух | + | '''Задача 1''' Из двух населенных пунктов А и В одновременно навстречу друг другу выходят два туриста. При встрече оказывается, что турист, вышедший из А, прошел на 2 км больше, чем второй турист. Продолжая движение с той же скоростью, первый турист прибывает в В через 1 ч 36 мин, а второй в А — через 2 ч 30 мин. Найдите расстояние АВ и скорость каждого туриста. |
| − | Решение. Построим графики движения туристов (рис. 1). | + | '''Решение.''' |
| + | Построим графики движения туристов (рис. 1). | ||
По условию задачи PR - PK =2, KC=1,6, RD=2,5; | По условию задачи PR - PK =2, KC=1,6, RD=2,5; | ||
| − | Нужно найти АВ, PR/АR, KP/ВК. Из подобия треугольников(ΔBKP ~ ΔDRP; ΔCKP~ΔARP) следует что КС:АR=КР: PR=ВК: RD но ВК=АR поэтому КС:АR= АR: RD или АR* АR=1,6*2,5; АR=2. Затем,1,6:2=PК: PК+2. Откуда PК=8 км, АВ=18км, v1 = 5км/ч, v2= 4 км/ч. | + | Нужно найти АВ, PR/АR, KP/ВК. Из подобия треугольников(ΔBKP ~ ΔDRP; ΔCKP~ΔARP) следует что КС:АR=КР: PR=ВК: RD но ВК=АR поэтому КС:АR= АR: RD или АR* АR=1,6*2,5; АR=2. Затем,1,6:2=PК: PК+2. Откуда PК=8 км, АВ=18км, v1 = 5км/ч, v2=4 км/ч. |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | которое математик бежал назад от момента, когда заметил ошибку, до того, как выудил шляпу) и DF (за которое он вернулся назад). По условию задачи | + | [[Изображение:grafik221.jpg]], |
| + | |||
| + | |||
| + | |||
| + | '''Задача 2.''' | ||
| + | Математик шел домой по берегу ручья против течения со скоростью в полтора раза большей, чем скорость течения, и держал в руках палку и шляпу. В некоторый момент он бросил в ручей шляпу, перепутав ее с палкой, и продолжал идти против течения ручья с той же скоростью. Через некоторое время он заметил ошибку, бросил палку в ручей и побежал назад со скоростью вдвое большей, чем шел ранее. Догнав плывущую шляпу, он мгновенно выудил ее из воды, повернулся и пошел против течения с первоначальной скоростью. Через 10 мин он встретил плывущую по ручью палку. На сколько раньше он пришел бы домой, если бы не перепутал палку со шляпой? | ||
| + | |||
| + | '''Решение.''' | ||
| + | |||
| + | Построим графики движения математика, палки и шляпы (рис. 2; сплошная линия соответствует движению математика, штриховая - движению шляпы и палки). | ||
| + | В момент В математик бросил шляпу, в момент С бросил палку и побежал назад, в момент D выудил шляпу, в момент Е встретил палку. Потерянное время состоит из CD (за которое математик бежал назад от момента, когда заметил ошибку, до того, как выудил шляпу) и DF (за которое он вернулся назад). По условию задачи | ||
vматем: vручья =ВР/АВ :РВ/ВD=3/2; vматем: v1 матем =КС/АС:КС/СD= СD/АС=1/2 | vматем: vручья =ВР/АВ :РВ/ВD=3/2; vматем: v1 матем =КС/АС:КС/СD= СD/АС=1/2 | ||
DE = BC=10; требуется определить CF. | DE = BC=10; требуется определить CF. | ||
| − | Пусть CD=x, тогда DF=AC=2x, АВ =2х+10. | + | Пусть CD=x, тогда DF=AC=2x, АВ =2х+10. |
| + | Имеем: (х+10) : (2х-10)=3/2. | ||
т.е. х=12,5мин; CF = CD + DF = x + 2Х = 37,5 мин. | т.е. х=12,5мин; CF = CD + DF = x + 2Х = 37,5 мин. | ||
Ответ: математик потерял 37,5 мин | Ответ: математик потерял 37,5 мин | ||
| − | Задача 3. Из А в В со | + | '''Задача 3.''' |
| + | Из А в В со скоростью 4 км/ч вышел турист. Спустя час вслед за ним из А вышел второй турист, проходивший в час 5 км, а еще через час из А выехал велосипедист, который, обогнав одного туриста, через 10 мин обогнал и другого. Найдите скорость велосипедиста. | ||
| − | Ре ш е н и е. | + | '''Ре ш е н и е.''' |
| − | + | ||
| − | + | ||
| − | + | Построим графики движения двух туристов и велосипедиста, предположив, что велосипедист сначала догоняет второго туриста (рис. 4). | |
| − | Рассмотрим теперь случай, когда | + | По условию задачи AC=CD = l, СС'=4, DD' = 5, EF = -1/6; надо найти РЕ /DЕ. Пусть DE=x.. Имеем РЕ: DF= РЕ: KF, причем РЕ = 5{1 + х), KF = 4 (2 1/6 + х), откуда |
| − | + | Х:( х+ 1/6)= 5{1 + х): 4(2 1/6 + х), получаем:6х2-17х+5=0, откуда х1=1/3 ч; х2= 2,5 ч; v1 = 20км/ч, v2= 7 км/ч. | |
| + | |||
| + | Рассмотрим теперь случай, когда велосипедист сначала догоняет первого туриста (рис 5). Имеем DE: DF= РЕ: KF, или Х:( х+ 1/6)= 4(2 + х): 5(1 1/6+х). Решив уравнение получим х= 3,2, v=6,5 км/ч. Возникают вопросы: как истолковать два ответа в первом случае? Почему во втором случае только один ответ? И здесь нам на помощь приходит график. Оказывается, велосипедист может ехать со скоростью 20 км/ч, догнать второго туриста и через 10 мин догнать первого (рис, 6). Но он может ехать медленнее, со скоростью 7 км/ч, и догнать, второго туриста позже, затем, также через 10 мин, догнать первого туриста. | ||
| + | Рис. 6 | ||
| − | Во втором случае (штриховая линия на рис. 6) догнать сначала первого туриста | + | Во втором случае (штриховая линия на рис. 6) догнать сначала первого туриста велосипедист может только после того, как второй турист обгонит первого. Но после этого события расстояние между туристами увеличивается и ни при какой другой скорости, отличной от найденной (л;6,5 км/ч), догнать за 10 мин второго туриста велосипедист не сможет. |
Ответ: 20 км/ч, или 7 км/ч, или 6,5км/ч. | Ответ: 20 км/ч, или 7 км/ч, или 6,5км/ч. | ||
| − | Задача 4. | + | '''Задача 4.''' |
| − | Решение. Построим графики движения велосипедиста и мотоциклиста (рис. 7). | + | Из пункта А в пункт В выехал велосипедист. В тот момент, когда он проехал 1/4 пути между А и В, из В в А выехал мотоциклист, который, прибыв в А, не задерживаясь, повернул обратно и одновременно с велосипедистом прибыл в В. Время движения мотоциклиста до первой встречи с велосипедистом равно времени движения мотоциклиста из А в В. Считая, что скорости мотоциклиста при движении из А в В и из В в А различны, найти, во сколько раз скорость мотоциклиста при движении из А в В больше скорости велосипедиста. |
| + | |||
| + | '''Решение.''' | ||
| + | Построим графики движения велосипедиста и мотоциклиста (рис. 7). | ||
По условию DP=1/4 АВ (отсюда АР = 1/4АТ); PK=LT; требуется найти QT/LT:QT/FT=АТ/LT | По условию DP=1/4 АВ (отсюда АР = 1/4АТ); PK=LT; требуется найти QT/LT:QT/FT=АТ/LT | ||
| − | + | Рис. 7 | |
Докажем (от противного), что мотоциклист прошел до первой встречи с велосипедистом | Докажем (от противного), что мотоциклист прошел до первой встречи с велосипедистом | ||
1/2 АВ, т. е. FC= 1/2АВ. Допустим, что FC<1/2АВ, тогда СК>1/2АВ. | 1/2 АВ, т. е. FC= 1/2АВ. Допустим, что FC<1/2АВ, тогда СК>1/2АВ. | ||
Время РК, за которое мотоциклист прошел расстояние FC, равно времени РК, за которое | Время РК, за которое мотоциклист прошел расстояние FC, равно времени РК, за которое | ||
| − | велосипедист прошел МС. Так как DP = 1/4AB, а СК> 1/2 АВ, то МС >1/4AB, следовательно, | + | велосипедист прошел МС. Так как DP = 1/4AB, а СК> 1/2 АВ, то МС >1/4AB, следовательно, велосипедист потратит больше времени на прохождение МС, чем на DP. Таким образом, |
| − | + | PK>AР=1/4 AT. | |
| − | Очевидно, CК>CF, следовательно, время KL, необходимое мотоциклисту для | + | Очевидно, CК>CF, следовательно, время KL, необходимое мотоциклисту для прохождения расстояния СК, больше времени РК, затраченного на прохождение FC. Таким образом, имеем: KL>PK>AP=1/4AT. Значит, на LT (время, за которое мотоциклист пройдет расстояние АВ) остается меньше 1/4AT. Отсюда РК не равно LT (РК >1/4 AT, LT< 1/4AT) что противоречит условию задачи. |
| − | Аналогично устанавливаем, что FC не | + | Аналогично устанавливаем, что FC не может быть больше1/2 АВ. Таким образом, доказано, что FC = 1/2 АВ, тогда АР=РК= KL=LT =1/4АТ и искомое отношение AT: LT=4 |
| − | Ответ: скорость мотоциклиста при | + | |
| − | В приведенных примерах использование | + | '''Ответ:''' скорость мотоциклиста при движении от А к В в 4 раза больше скорости велосипедиста. |
| − | Нередко, используя графики, можно | + | |
| − | Кроме того, следует учитывать | + | В приведенных примерах использование графиков приводит к простым и красивым решениям. Кроме того, этот способ является прекрасным средством реализации межпредметных связей между алгеброй, геометрией и физикой. Строя график зависимости пройденного расстояния от времени (при равномерном движении), учащиеся вспоминают, что эта зависимость выражается линейной функцией, повторяют физический смысл углового коэффициента прямой, используют при решении текстовых алгебраических задач равенство и подобие треугольников. При этом знания, полученные на уроках по разным предметам, объединяются, становятся более осознанными, действенными. Абстрактные графики, изучаемые в алгебре, наполняются новым содержанием, конкретизируются в ходе познавательной деятельности учащихся. |
| − | Очевидно, что использование | + | Нередко, используя графики, можно увидеть «скрытые» свойства рассматриваемых величин: шляпа и палка (задача 2) проплыли равные расстояния (PB = LN, см. рис. 2), на встречу с палкой математик затратил столько же минут, сколько и на удаление от шляпы (BC=DE; эти выводы являются очевидными следствиями того факта, что прямые, изображающие графики движений с одинаковыми скоростями, параллельны); мотоциклист (задача 5) встретил первый раз велосипедиста на 1/2 пути, скорость мотоциклиста до первой встречи в два раза больше, чем скорость велосипедиста, и др. |
| − | Литература | + | Кроме того, следует учитывать индивидуальные особенности учащихся. Алгебраические решения ближе тем, кто любит формулы, их преобразования; решения с использованием графиков привлекают тех, кто нуждается в содержательных образах, кто любит геометрию, физику. |
| + | Очевидно, что использование описанного метода требует определенных навыков графического представления условий задачи. Они могут быть сформированы совместными усилиями учителей физики и математики. Затраченные усилия быстро окупятся. | ||
| + | [[Изображение:grafik220.jpg]], | ||
| + | |||
| + | '''Литература''' | ||
| + | |||
1. Алгебра7 под ред. С.А.Теляковского. М.Просвещение. 1985г. | 1. Алгебра7 под ред. С.А.Теляковского. М.Просвещение. 1985г. | ||
| + | |||
2. Квант. 1970. №6,стр. 47-88 | 2. Квант. 1970. №6,стр. 47-88 | ||
| + | |||
3. Энциклопедический словарь юного математика. М. Педагогика. 1985г. | 3. Энциклопедический словарь юного математика. М. Педагогика. 1985г. | ||
| + | |||
| + | [[Категория: Проект ДООМ - 2008-2009]] | ||
Текущая версия на 10:51, 19 ноября 2008
Использование графиков равномерного движения при решении текстовых задач по алгебре.
Обычно при решении текстовых задач на движение для наглядности пройденное расстояние изображают отрезком, однако это не всегда упрощает решение. Указанный недостаток можно устранить, применяя графическое представление движения, известное учащимся из курса физики. Отметим, что при решении задач на равномерное движение полезны соотношения:
S1 : S2 =t1 : t2 – если скорости равны;
V1 : V2 =t1 : t2 – если равны пройденные расстояния;
S1 : S2 = V1 : V2 – если равны промежутки времени;
Кроме того, известно, что тангенс угла наклона прямой x=х0 +Vt к оси Ot численно равен скорости тела. Рассмотрим решение нескольких задач, используя график равномерного движения.
Задача 1 Из двух населенных пунктов А и В одновременно навстречу друг другу выходят два туриста. При встрече оказывается, что турист, вышедший из А, прошел на 2 км больше, чем второй турист. Продолжая движение с той же скоростью, первый турист прибывает в В через 1 ч 36 мин, а второй в А — через 2 ч 30 мин. Найдите расстояние АВ и скорость каждого туриста. Решение. Построим графики движения туристов (рис. 1). По условию задачи PR - PK =2, KC=1,6, RD=2,5; Нужно найти АВ, PR/АR, KP/ВК. Из подобия треугольников(ΔBKP ~ ΔDRP; ΔCKP~ΔARP) следует что КС:АR=КР: PR=ВК: RD но ВК=АR поэтому КС:АR= АR: RD или АR* АR=1,6*2,5; АR=2. Затем,1,6:2=PК: PК+2. Откуда PК=8 км, АВ=18км, v1 = 5км/ч, v2=4 км/ч.
Задача 2. Математик шел домой по берегу ручья против течения со скоростью в полтора раза большей, чем скорость течения, и держал в руках палку и шляпу. В некоторый момент он бросил в ручей шляпу, перепутав ее с палкой, и продолжал идти против течения ручья с той же скоростью. Через некоторое время он заметил ошибку, бросил палку в ручей и побежал назад со скоростью вдвое большей, чем шел ранее. Догнав плывущую шляпу, он мгновенно выудил ее из воды, повернулся и пошел против течения с первоначальной скоростью. Через 10 мин он встретил плывущую по ручью палку. На сколько раньше он пришел бы домой, если бы не перепутал палку со шляпой?
Решение.
Построим графики движения математика, палки и шляпы (рис. 2; сплошная линия соответствует движению математика, штриховая - движению шляпы и палки). В момент В математик бросил шляпу, в момент С бросил палку и побежал назад, в момент D выудил шляпу, в момент Е встретил палку. Потерянное время состоит из CD (за которое математик бежал назад от момента, когда заметил ошибку, до того, как выудил шляпу) и DF (за которое он вернулся назад). По условию задачи vматем: vручья =ВР/АВ :РВ/ВD=3/2; vматем: v1 матем =КС/АС:КС/СD= СD/АС=1/2 DE = BC=10; требуется определить CF. Пусть CD=x, тогда DF=AC=2x, АВ =2х+10. Имеем: (х+10) : (2х-10)=3/2. т.е. х=12,5мин; CF = CD + DF = x + 2Х = 37,5 мин. Ответ: математик потерял 37,5 мин
Задача 3. Из А в В со скоростью 4 км/ч вышел турист. Спустя час вслед за ним из А вышел второй турист, проходивший в час 5 км, а еще через час из А выехал велосипедист, который, обогнав одного туриста, через 10 мин обогнал и другого. Найдите скорость велосипедиста.
Ре ш е н и е.
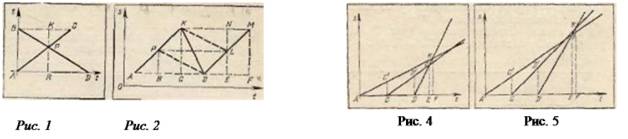
Построим графики движения двух туристов и велосипедиста, предположив, что велосипедист сначала догоняет второго туриста (рис. 4). По условию задачи AC=CD = l, СС'=4, DD' = 5, EF = -1/6; надо найти РЕ /DЕ. Пусть DE=x.. Имеем РЕ: DF= РЕ: KF, причем РЕ = 5{1 + х), KF = 4 (2 1/6 + х), откуда Х:( х+ 1/6)= 5{1 + х): 4(2 1/6 + х), получаем:6х2-17х+5=0, откуда х1=1/3 ч; х2= 2,5 ч; v1 = 20км/ч, v2= 7 км/ч.
Рассмотрим теперь случай, когда велосипедист сначала догоняет первого туриста (рис 5). Имеем DE: DF= РЕ: KF, или Х:( х+ 1/6)= 4(2 + х): 5(1 1/6+х). Решив уравнение получим х= 3,2, v=6,5 км/ч. Возникают вопросы: как истолковать два ответа в первом случае? Почему во втором случае только один ответ? И здесь нам на помощь приходит график. Оказывается, велосипедист может ехать со скоростью 20 км/ч, догнать второго туриста и через 10 мин догнать первого (рис, 6). Но он может ехать медленнее, со скоростью 7 км/ч, и догнать, второго туриста позже, затем, также через 10 мин, догнать первого туриста. Рис. 6
Во втором случае (штриховая линия на рис. 6) догнать сначала первого туриста велосипедист может только после того, как второй турист обгонит первого. Но после этого события расстояние между туристами увеличивается и ни при какой другой скорости, отличной от найденной (л;6,5 км/ч), догнать за 10 мин второго туриста велосипедист не сможет. Ответ: 20 км/ч, или 7 км/ч, или 6,5км/ч.
Задача 4.
Из пункта А в пункт В выехал велосипедист. В тот момент, когда он проехал 1/4 пути между А и В, из В в А выехал мотоциклист, который, прибыв в А, не задерживаясь, повернул обратно и одновременно с велосипедистом прибыл в В. Время движения мотоциклиста до первой встречи с велосипедистом равно времени движения мотоциклиста из А в В. Считая, что скорости мотоциклиста при движении из А в В и из В в А различны, найти, во сколько раз скорость мотоциклиста при движении из А в В больше скорости велосипедиста.
Решение. Построим графики движения велосипедиста и мотоциклиста (рис. 7). По условию DP=1/4 АВ (отсюда АР = 1/4АТ); PK=LT; требуется найти QT/LT:QT/FT=АТ/LT Рис. 7
Докажем (от противного), что мотоциклист прошел до первой встречи с велосипедистом 1/2 АВ, т. е. FC= 1/2АВ. Допустим, что FC<1/2АВ, тогда СК>1/2АВ. Время РК, за которое мотоциклист прошел расстояние FC, равно времени РК, за которое велосипедист прошел МС. Так как DP = 1/4AB, а СК> 1/2 АВ, то МС >1/4AB, следовательно, велосипедист потратит больше времени на прохождение МС, чем на DP. Таким образом, PK>AР=1/4 AT. Очевидно, CК>CF, следовательно, время KL, необходимое мотоциклисту для прохождения расстояния СК, больше времени РК, затраченного на прохождение FC. Таким образом, имеем: KL>PK>AP=1/4AT. Значит, на LT (время, за которое мотоциклист пройдет расстояние АВ) остается меньше 1/4AT. Отсюда РК не равно LT (РК >1/4 AT, LT< 1/4AT) что противоречит условию задачи. Аналогично устанавливаем, что FC не может быть больше1/2 АВ. Таким образом, доказано, что FC = 1/2 АВ, тогда АР=РК= KL=LT =1/4АТ и искомое отношение AT: LT=4
Ответ: скорость мотоциклиста при движении от А к В в 4 раза больше скорости велосипедиста.
В приведенных примерах использование графиков приводит к простым и красивым решениям. Кроме того, этот способ является прекрасным средством реализации межпредметных связей между алгеброй, геометрией и физикой. Строя график зависимости пройденного расстояния от времени (при равномерном движении), учащиеся вспоминают, что эта зависимость выражается линейной функцией, повторяют физический смысл углового коэффициента прямой, используют при решении текстовых алгебраических задач равенство и подобие треугольников. При этом знания, полученные на уроках по разным предметам, объединяются, становятся более осознанными, действенными. Абстрактные графики, изучаемые в алгебре, наполняются новым содержанием, конкретизируются в ходе познавательной деятельности учащихся.
Нередко, используя графики, можно увидеть «скрытые» свойства рассматриваемых величин: шляпа и палка (задача 2) проплыли равные расстояния (PB = LN, см. рис. 2), на встречу с палкой математик затратил столько же минут, сколько и на удаление от шляпы (BC=DE; эти выводы являются очевидными следствиями того факта, что прямые, изображающие графики движений с одинаковыми скоростями, параллельны); мотоциклист (задача 5) встретил первый раз велосипедиста на 1/2 пути, скорость мотоциклиста до первой встречи в два раза больше, чем скорость велосипедиста, и др.
Кроме того, следует учитывать индивидуальные особенности учащихся. Алгебраические решения ближе тем, кто любит формулы, их преобразования; решения с использованием графиков привлекают тех, кто нуждается в содержательных образах, кто любит геометрию, физику.
Очевидно, что использование описанного метода требует определенных навыков графического представления условий задачи. Они могут быть сформированы совместными усилиями учителей физики и математики. Затраченные усилия быстро окупятся.
 ,
,
Литература
1. Алгебра7 под ред. С.А.Теляковского. М.Просвещение. 1985г.
2. Квант. 1970. №6,стр. 47-88
3. Энциклопедический словарь юного математика. М. Педагогика. 1985г.