Семинар ДООМ Прямоугольный параллелепипед
Проба (обсуждение | вклад) |
Проба (обсуждение | вклад) |
||
| (не показаны 2 промежуточные версии 1 участника) | |||
| Строка 1: | Строка 1: | ||
'''Автор: Рыскалкина Наталия Васильевна IDm005''' | '''Автор: Рыскалкина Наталия Васильевна IDm005''' | ||
| − | + | <br> Команда [[Участник:IDm005 ТАНГРАМ ]] | |
'''Тема урока: Прямоугольный параллелепипед.''' | '''Тема урока: Прямоугольный параллелепипед.''' | ||
| Строка 53: | Строка 53: | ||
'''5. Самостоятельная работа (в двух вариантах).''' | '''5. Самостоятельная работа (в двух вариантах).''' | ||
| + | <br>[[Изображение:Самостоятельная работа.jpg]], | ||
<br>6. '''Домашнее задание:''' параграф 50, № 910,912,913. | <br>6. '''Домашнее задание:''' параграф 50, № 910,912,913. | ||
<br>7. '''Итог урока.''' | <br>7. '''Итог урока.''' | ||
Текущая версия на 22:52, 10 ноября 2009
Автор: Рыскалкина Наталия Васильевна IDm005
Команда Участник:IDm005 ТАНГРАМ
Тема урока: Прямоугольный параллелепипед.
Тип урока: формирование новых знаний.
Форма проведения: эвристическая беседа.
Цели урока:
1) ознакомить учащихся с многообразием геометрических тел, в частности с прямоугольным параллелепипедом;
2) систематизировать знания о параллелепипеде, кубе;
3) развитие пространственного воображения и пространственного представления;
4) научить анализировать полученные данные и делать выводы;
5) привитие интереса к изучению математики.
Оборудование: модели прямоугольного параллелепипеда, многогранники и тела вращения.
Оформление доски: высказывание А.С.Пушкина, перевод с греческого слова «параллелепипед», рисунки прямоугольных параллелепипедов.
Ход урока:
1. Организационный момент.
Великий русский поэт А.С.Пушкин считал, что «вдохновение нужно в поэзии, как в геометрии». И Пушкин был прав. Без
вдохновения Пушкин не смог бы написать столь гениальные стихи. И без вдохновения невозможно успешно изучать такой раздел
математики как геометрия. Сегодня у нас на уроке геометрический материал. Начнем же его изучение с вдохновением!
2. Вводная беседа.
Нас окружает множество предметов. Они отличаются формой, размерами, материалом, из которого изготовлены, окраской… Людей
обычно интересуют разные качества этих предметов. Математиков же интересуют только их форма и размеры, поэтому они изучают
не сами предметы, а их формы. В геометрии вместо предметов мы будем рассматривать геометрические темы.
3. Новый материал.
- Рассмотрим два семейства геометрических тел: многогранники и «круглые тела».
- По какому признаку эти геометрические тела разбиты на две группы?
- Представителем семейства многогранников является прямоугольный параллелепипед. Свое название он получил от слов:
параллелос – «идущие рядом», эпидос – «плоскость».
- Рассмотрев модели прямоугольного параллелепипеда на столах, объясните почему он получил такое название?
- Из чего состоит поверхность прямоугольного параллелепипеда? (ввести понятия граней, ребер, вершин)
- На моделях подсчитайте количество граней, ребер, вершин.
- Среди граней нет ли равных? Сколько пар?
- Сколько достаточно выполнить измерений, чтобы найти длины всех ребер?
- Покажите ребра исходящие из одной вершины.
- Как называют эти ребра? ( длина, ширина, высота или измерения) находим определение измерений в учебнике.( измерения
прямоугольного параллелепипеда – это длины трех ребер исходящих из одной вершины.)
- Как называют прямоугольный параллелепипед, у которого все ребра равны? Дайте определение куба.
- Решим задачу про куб. № 909 из учебника: у куба отрезаем угол. Сколько граней у получившегося многогранника? Какую
форму он имеет? ( рис. 98 учебника )
- Рассмотрим изображение прямоугольного параллелепипеда ( без штрихованных линий, на доске). На таком рисунке мы видим набор линий, в котором трудно разобраться. В геометрии, принято линии, скрытые от глаз наблюдателя, изображать не сплошными, а штрихованными.( на проволочной модели рассмотреть видимые, невидимые линии. Затем на рисунке провести штрихованные линии).
- Изобразим в тетрадях прямоугольный параллелепипед, измерения которого равны 4 см; 5 см; 6 см. Для этого: 1) переднюю
грань изображаем без изменения формы и размеров. 2) ребра верхней и нижней граней проводим под углом 450 или 1350 к ним и
длиной вдвое меньше, чем в действительности. 3) невидимые линии изображаем штрихованными линиями.
4. Закрепление изученного материала.
1) По рисунку назвать вершины, равные ребра.( обозначение одинаковым количеством черточек)
2) Назвать видимые и невидимые грани на рисунке. Какая грань к нам ближе? Какое ребро?
3)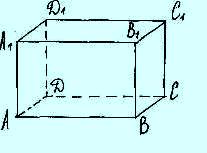 ,
,
4) какие изображения правильные?
5. Самостоятельная работа (в двух вариантах).
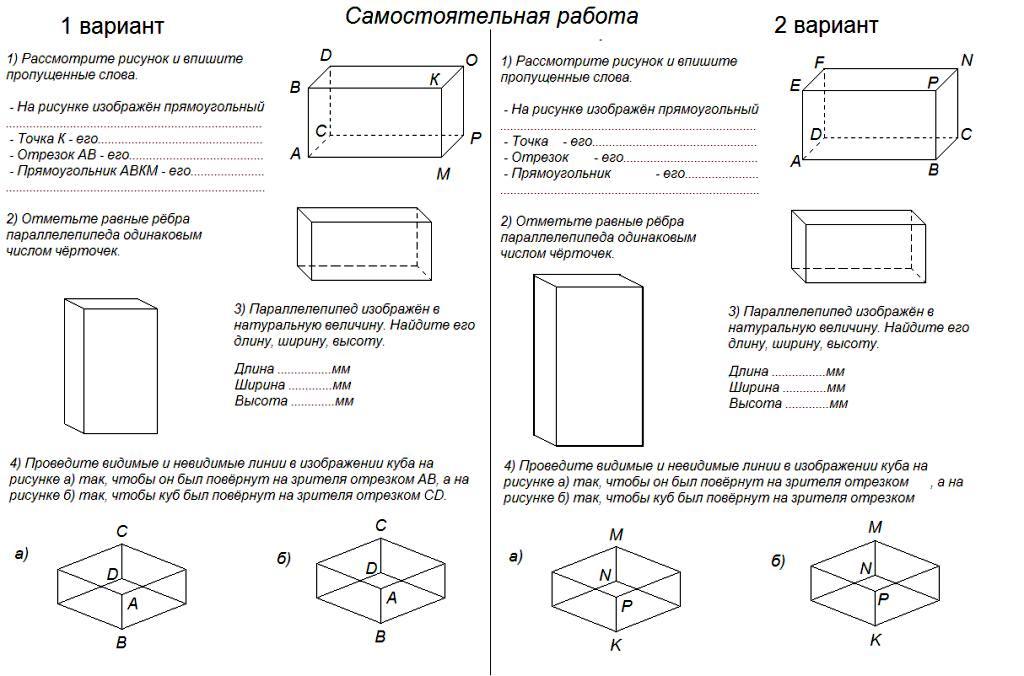 ,
,
6. Домашнее задание: параграф 50, № 910,912,913.
7. Итог урока.

