Семинар ДООМ Параллельность прямых
| (не показаны 2 промежуточные версии 1 участника) | |||
| Строка 22: | Строка 22: | ||
'''Воспитательная:''' воспитывать у детей внимательность, аккуратность и понимание того, что надо учиться аргументировано отстаивать свою точку зрения. | '''Воспитательная:''' воспитывать у детей внимательность, аккуратность и понимание того, что надо учиться аргументировано отстаивать свою точку зрения. | ||
| − | <center>Ход урока.</center> | + | <center>'''''Ход урока.'''''</center> |
'''1.Организационный момент (1мин.)''' | '''1.Организационный момент (1мин.)''' | ||
| Строка 29: | Строка 29: | ||
На доске нарисованы четырехугольники | На доске нарисованы четырехугольники | ||
| + | [[Изображение:IMGfigur.jpg]] | ||
Вспомним название этих четырехугольников. Проведем прямые, лежащие на сторонах данных четырехугольников. Замечаем, что если продлить стороны трапеции, то две противоположные стороны пересекутся, а две другие – нет. У параллелограмма и прямоугольника противоположные стороны не пересекутся. | Вспомним название этих четырехугольников. Проведем прямые, лежащие на сторонах данных четырехугольников. Замечаем, что если продлить стороны трапеции, то две противоположные стороны пересекутся, а две другие – нет. У параллелограмма и прямоугольника противоположные стороны не пересекутся. | ||
| Строка 38: | Строка 39: | ||
Докажем параллельность противоположных сторон прямоугольника, предварительно рассмотрев следующие рисунки: | Докажем параллельность противоположных сторон прямоугольника, предварительно рассмотрев следующие рисунки: | ||
| − | + | <table> | |
| + | <tr> | ||
| + | <td> | ||
| + | [[Изображение:IMGpryam.jpg|thumb|''Рис. 1. Длинные косые линии этой фигуры параллельны, хотя кажутся расходящимися. '']] | ||
| + | </table> | ||
| + | <table> | ||
| + | <tr> | ||
| + | <td> | ||
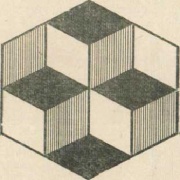
| + | [[Изображение:IMGkub.jpg|thumb|''Рис. 2. При рассмотрении этой фигуры будут казаться выступающими вперед поочередно то два куба вверху, то два куба внизу.'']] | ||
| + | </tr> | ||
| + | </table> | ||
Эффект от работы с этим рисунком поразителен. На вопрос сверху один куб, а снизу два – ответ утвердительный. А может сверху два куба, а снизу один – опять утвердительный ответ. | Эффект от работы с этим рисунком поразителен. На вопрос сверху один куб, а снизу два – ответ утвердительный. А может сверху два куба, а снизу один – опять утвердительный ответ. | ||
После работы с рисунками, когда дети действительно убеждаются, что не всегда можно «верить своим глазам», переходим к доказательству. | После работы с рисунками, когда дети действительно убеждаются, что не всегда можно «верить своим глазам», переходим к доказательству. | ||
| Строка 58: | Строка 69: | ||
''III.Математический диктант'' | ''III.Математический диктант'' | ||
| − | Пишут под копирку, первый листок сдается, а по второму проверяется правильность выполнения, сверяя с образцом решения, заранее вынесенным на доску | + | Пишут под копирку, первый листок сдается, а по второму проверяется правильность выполнения, сверяя с образцом решения, заранее вынесенным на доску. |
I вариант | I вариант | ||
| Строка 81: | Строка 92: | ||
'''7. Рефлексия урока (1 мин.)''' | '''7. Рефлексия урока (1 мин.)''' | ||
| + | |||
| + | [[Категория: Проект ДООМ 2009-2010]] | ||
Текущая версия на 21:36, 1 декабря 2009
Участник:Яковлева Надежда Васильевна
Команда: ТреугольникIDm040
На первых уроках геометрии, объясняя ту или иную теорему, часто слышишь от детей: «Что тут доказывать и так все видно!». Поэтому чтобы не было непонимания, на уроках математики в 5, 6 классах, когда мы изучаем геометрический материал и дети только начинают осознавать, что есть такая область математики – геометрия, я им рассказываю об оптических обманах. Не все то, что мы видим, является таковым на самом деле. А вот доказать то или иное утверждение можно при помощи рассуждений. Так, в 6 классе, при изучении темы «Параллельность прямых» дети получают первый опыт по доказательству математических утверждений.
Учитель математики: Яковлева Н.В.
Класс: 6
Оборудование: рисунки, модели кубов, прямоугольных параллелепипедов.
Тема урока. Параллельность прямых.
Тип урока: комбинированный
Цели урока:
Обучающая: знать какие прямые называются параллельными; уметь находить отрезки параллельных прямых среди предметов окружающей обстановки, строить прямую, параллельную данной.
Развивающая: получить первый опыт доказательства математических утверждений;
Воспитательная: воспитывать у детей внимательность, аккуратность и понимание того, что надо учиться аргументировано отстаивать свою точку зрения.
1.Организационный момент (1мин.)
2.Повторение ранее изученного материала (4 мин.)
На доске нарисованы четырехугольники
Вспомним название этих четырехугольников. Проведем прямые, лежащие на сторонах данных четырехугольников. Замечаем, что если продлить стороны трапеции, то две противоположные стороны пересекутся, а две другие – нет. У параллелограмма и прямоугольника противоположные стороны не пересекутся.
3.Объяснение нового материала (10 мин.).
Вводится определение параллельных прямых. Параллельные прямые встречаются так же часто, как и перпендикулярные. Например, в любом прямоугольнике противоположные стороны лежат на параллельных прямых. Докажем параллельность противоположных сторон прямоугольника, предварительно рассмотрев следующие рисунки:
Эффект от работы с этим рисунком поразителен. На вопрос сверху один куб, а снизу два – ответ утвердительный. А может сверху два куба, а снизу один – опять утвердительный ответ. После работы с рисунками, когда дети действительно убеждаются, что не всегда можно «верить своим глазам», переходим к доказательству.
4.Закрепление полученных знаний. (23 мин.)
I. Устные упражнения
- Назовите отрезки параллельных прямых среди предметов окружающей обстановки.
- На моделях куба, прямоугольного параллелепипеда укажите параллельные прямые, на которых лежат ребра. Сколько таких пар параллельных прямых?
- При планировке городов используют параллельность прямых. Так в Тольятти, в Автозаводском районе, какие улицы параллельны друг другу?
- Упр. № 149 (А.Г. Мордкович)
Выставляются оценки.
II.Практическая часть
- Дана прямая и точка вне этой прямой. Сколько прямых, параллельных данной, можно провести через точку. Сначала прямую проводим от руки тонкой линией, а потом строим с помощью чертежных инструментов.
- Упр. № 147 (а, б) (А.Г. Мордкович) Оцениваются работы 5-6 учеников, которые помогают справиться с заданием остальным учащимся.
III.Математический диктант
Пишут под копирку, первый листок сдается, а по второму проверяется правильность выполнения, сверяя с образцом решения, заранее вынесенным на доску.
I вариант
- Как называются две прямые, лежащие в одной плоскости и не имеющие общих точек?
- Начертите две параллельные прямые АЕ и РК.
- Прямые АС и ВС перпендикулярны прямой МТ. Каково взаимное расположение прямых АС и ВС?
- Запишите с помощью символов: прямые АВ и СМ параллельны.
- Проведите прямую АВ ; отметьте точку К вне этой прямой. Проведите через К прямую, параллельную прямой АВ.
II вариант
- Начертите две параллельные прямые АВ и МК.
- Как называются две прямые, лежащие в одной плоскости и не имеющие общих точек?
- Прямые ВС и КМ перпендикулярны ОР. Каково взаимное расположение прямых ВС и КМ?
- Запишите с помощью символов: прямые СЕ и ВМ параллельны.
- Проведите прямую СМ; отметьте точку К вне этой прямой. Проведите через К прямую, параллельную прямой СМ.
6.Итог урока (1 мин).
Оценка за математический диктант сообщается на следующем уроке, хотя дети уже знают предварительно свою оценку и какие ошибки они допустили.
На дом: упр. № 147 (в, г), № 150.
7. Рефлексия урока (1 мин.)