Семинар ДООМ Применение методов визуализации
м («Применение методов визуализации» переименована в «Семинар ДООМ Применение методов визуализации») |
|||
| (не показана 1 промежуточная версия 1 участника) | |||
| Строка 46: | Строка 46: | ||
:1. Работа учителя со всем классом. | :1. Работа учителя со всем классом. | ||
| − | Учитель говорит, что ученикам предстоит изучить два важнейших класса преобразований: движения и подобия. Движения - это те преобразования фигур, которые сохраняют расстояния между точками. Пример для учеников: на листе бумаги отметить две точки, измерить расстояние между ними, переместить лист и снова измерить расстояние. Важность движений в том, что при движениях фигура сохраняет свою форму и все свои размеры, поскольку все геометрические величины можно выразить через расстояния. Ученики вспоминают формулы, выражающие различные величины через дайны (для площадей, для углов - тригонометрия, для объемов) и утверждения о равенстве фигур, имеющих соответственно равные линейные размеры (треугольников - по трем сторонам, прямоугольников - по их измерениям, окружностей - по радиусам). | + | :Учитель говорит, что ученикам предстоит изучить два важнейших класса преобразований: движения и подобия. Движения - это те |
| − | Далее конкретизируется общее утверждение о том, что движение сохраняет все свойства фигур! Ключевым здесь является предложение о том, что при движении образом отрезка является отрезок. Многие фигуры конструируются из отрезков: отрезки вытягиваются в лучи, в прямые. Отрезками «заметаются» треугольники (см. рис. 2). | + | преобразования фигур, которые сохраняют расстояния между точками. Пример для учеников: на листе бумаги отметить две точки, измерить расстояние между ними, переместить лист и снова измерить расстояние. Важность движений в том, что при движениях фигура сохраняет свою форму и все свои размеры, поскольку все геометрические величины можно выразить через расстояния. Ученики вспоминают формулы, выражающие различные величины через дайны (для площадей, для углов - тригонометрия, для объемов) и утверждения о равенстве фигур, имеющих соответственно равные линейные размеры (треугольников - по трем сторонам, прямоугольников - по их измерениям, окружностей - по радиусам). |
| + | |||
| + | [[Изображение:Ф_ПМ.jpg|300px|]] | ||
| + | |||
| + | |||
| + | :Далее конкретизируется общее утверждение о том, что движение сохраняет все свойства фигур! Ключевым здесь является | ||
| + | предложение о том, что при движении образом отрезка является отрезок. Многие фигуры конструируются из отрезков: отрезки вытягиваются в лучи, в прямые. Отрезками «заметаются» треугольники (см. рис. 2). | ||
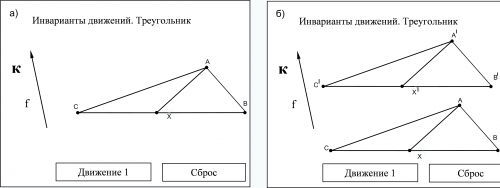
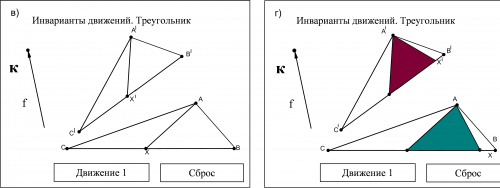
Эта и другие динамические модели, входящие в состав инновационного учебно-методического комплекса, как уже отмечаюсь выше, выполнены на основе Flash-технологий [3]. На рис. 2 а-г представлен экранный интерфейс модели в окне Web-браузера на различных этапах работы с ней пользователя. Модель служит для иллюстрации следующего утверждения: образом треугольника при движении является равный ему треугольник. В исходном состоянии в окне модели изображён исходный треугольник ABC и точка X на стороне ВС (рис. 2 а). Вершины треугольника можно перемещать произвольно, а точку X - вдоль стороны ВС (при этом закрашивается соответствующая область треугольника). В левой части окна изображён вектор с вершиной К, задающий некоторое движение f. Точка К является активной. С ее помощью можно изменять направление этого движения. При нажатии кнопки "Движение f" точки А, В и С переводятся соответственно в точки А', В' и С' (рис. 2 б). При этом в окне модели появляется образ треугольника А'В'С', который можно произвольным образом вращать курсором мыши (рис. 2 в). Этим же движением f отрезки АХ переводятся в отрезки А'Х' заполняющие треугольник А' В' С'. Этот про¬цесс можно наблюдать в интерактивном режиме, перемещая активную точку X вдоль стороны ВС (рис. 2 г). Кнопка «Сброс» в правом нижнем углу окна возвращает модель в исходное состояние. | Эта и другие динамические модели, входящие в состав инновационного учебно-методического комплекса, как уже отмечаюсь выше, выполнены на основе Flash-технологий [3]. На рис. 2 а-г представлен экранный интерфейс модели в окне Web-браузера на различных этапах работы с ней пользователя. Модель служит для иллюстрации следующего утверждения: образом треугольника при движении является равный ему треугольник. В исходном состоянии в окне модели изображён исходный треугольник ABC и точка X на стороне ВС (рис. 2 а). Вершины треугольника можно перемещать произвольно, а точку X - вдоль стороны ВС (при этом закрашивается соответствующая область треугольника). В левой части окна изображён вектор с вершиной К, задающий некоторое движение f. Точка К является активной. С ее помощью можно изменять направление этого движения. При нажатии кнопки "Движение f" точки А, В и С переводятся соответственно в точки А', В' и С' (рис. 2 б). При этом в окне модели появляется образ треугольника А'В'С', который можно произвольным образом вращать курсором мыши (рис. 2 в). Этим же движением f отрезки АХ переводятся в отрезки А'Х' заполняющие треугольник А' В' С'. Этот про¬цесс можно наблюдать в интерактивном режиме, перемещая активную точку X вдоль стороны ВС (рис. 2 г). Кнопка «Сброс» в правом нижнем углу окна возвращает модель в исходное состояние. | ||
Из треугольников составляются многоугольники, из тетраэдров - многогранники. | Из треугольников составляются многоугольники, из тетраэдров - многогранники. | ||
:Удобно для свойств, сохраняющихся для рассматриваемых преобразований, ввести термин инварианты преобразований. | :Удобно для свойств, сохраняющихся для рассматриваемых преобразований, ввести термин инварианты преобразований. | ||
Этот термин позволяет более кратко формулировать предложения о сохраняющихся свойствах. | Этот термин позволяет более кратко формулировать предложения о сохраняющихся свойствах. | ||
| + | |||
| + | [[Изображение:Тр2 ПМ.PNG|500px|]] | ||
| + | [[Изображение:Тр3_ПМ.png|500px|]] | ||
| + | |||
'''2. Самостоятельная работа учеников.''' | '''2. Самостоятельная работа учеников.''' | ||
| Строка 62: | Строка 72: | ||
:Апробация разработанных учебно-методических материалов, проведенная в ряде российских школ, показала повышение интереса | :Апробация разработанных учебно-методических материалов, проведенная в ряде российских школ, показала повышение интереса | ||
учащихся к предмету и высокую эффективность использования интерактивных компьютерных моделей. | учащихся к предмету и высокую эффективность использования интерактивных компьютерных моделей. | ||
| + | |||
| + | [[Изображение:Тетрадь_ПМ.gif|300px|]] | ||
| + | |||
'''Литература''' | '''Литература''' | ||
Текущая версия на 16:14, 8 декабря 2009
технический консультант Корнева Нина Алексеевна Команды: Участник: АксиомаIDm014,Участник: ТеоремикиIDm013,Участник: БесконечностьIDm029
Данная статья,представленная вашему вниманию, взята из журнала "Компьютерные инструменты в школе". №4 Санкт-Петербург 2008 год. Подписка на журнал была подарена нашей школе за прекрасные результаты в конкурсе.

Вернер Алексей Леонидович, Никитин Александр Борисович, Поздняков Сергей Николаевич, Рыжик Валерий Идельявич, Цикин Игорь Анатольевич
- Использование методов визуализации при создании учебно-методических материалов само по себе далеко не ново. С развитием
информационных технологий расширяются формы визуализации, улучшается качество результирующих учебных продуктов. Однако существенное усиление образовательного эффекта внедрения таких материалов должно дать создание именно интерактивных обучающих материалов, сочетающих в себе преимущества продуктивного воздействия на человека через визуальный канал поступления информации с эффективностью интерактивного взаимодействия учащегося с изучаемым материалом.
- Многие столетия курс элементарной геометрии был наиболее стабильным среди всех предметов в средней школе как по содержанию,
так и по методике его изучения: содержание его шло от «Начал» Евклида, а методика состояла, в основном, в изложении доказательств теорем учителем, которые затем подкреплялись решением задач учениками. Единственными учебными средствами были учебник и задачник к нему (или учебник, в котором, помимо теоретического материала, были и задачи).
- В последние десятилетия XX века положение стало меняться: в курсе геометрии появились новые разделы - векторы, координаты,
преобразования, а в начале XXI века для изучения геометрии стали применяться компьютерные средства.
- В курсе геометрии в 7 и 8 классах важнейшие теоремы доказывались традиционными синтетическими методами классической
элементарной геометрии. Геометрия в этих классах, в основном, статична: изучаются свойства заданных фигур, сравниваются их элементы, например, стороны и углы треугольников. В 9 классе курс геометрии начинает знакомить школьников с понятиями и методами математики, появившимися в XVII-XX вв.; координатами и методом координат, векторами и векторным методом, преобразованиями и методами преобразований. Они появились в школьном курсе геометрии в «посткиселевскую» эпоху в середине XX века. Можно было бы систематический школьный курс элемен¬тарной евклидовой геометрии построить на базе каждого из этих трех методов: как аналитическую геометрию (по Р. Декарту), как векторную геометрию (по Г. Вейлю) или как геометрию группы преобразований (по Ф. Клейну или по Ф. Бахману).
- Попытки построения курса геометрии в школе, изначально базирующегося на этих методах, не увенчались успехом (в начале
систематического курса геометрии сейчас все-таки лежат традиционные синтетические методы), но знакомить школьников, уже овладевших важнейшими фактами классической элементарной геометрии, с современными идеями и методами математики необходимо, поскольку (как неоднократно писал академик А.Д. Александров), школьный курс геометрии должен быть причастен к современной науке. Девятый класс - промежуточный между основной и старшей школой - наиболее подходящее место для такого знакомства: сравнение традиционных и современных методов при решении ими однотипных задач элементарной геометрии полезно и показывает школьникам, что и такая древняя наука, как геометрия, даже в школьном курсе постоянно развивается и обогащается. Именно поэтому авторы выбрали геометрию девятого класса в качестве объекта применения компьютерных инструментов при ее изучении. Разработанные авторами учебно-методические материалы включают в себя три составляющие: во-первых, учебное пособие по курсу геометрии для 9 класса, во-вторых, три рабочие тетради к этому курсу и, в-третьих, книгу для учителя. Содержание учебника ориентируется на содержание двух ранее изданных учебных пособий [1, 2].
- Каждая из этих составляющих представлена как в полиграфическом, так и в электронном варианте. Полиграфический вариант
вполне традиционен, а в его электронном варианте многие иллюстрации «оживают», становятся динамичными, что, конечно, и в дидактическом и в эстетическом смысле дает положительный эффект. Множество разнообразных динамических моделей включено во все разделы электронного учебного пособия, а электронные рабочие тетради состоят из интерактивных заданий, предназначенных для решения учащимися задач различного уровня сложности и выполнения самостоятельной работы. Электронные версии учебного пособия и рабочих тетрадей выполнены на основе широкого использования Flash - и Java-технологий [3, 4].
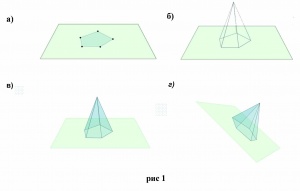
- Внешний вид одной из таких моделей в различных режимах ее работы приведен в качестве примера на рис. 1. Рассматриваемая
модель (технология Flash) позволяет в динамике визуализировать процесс построения пирамиды. В исходном состоянии в окне модели отображается плоскость, на которой пользователь может строить многоугольник - основание пирамиды. Построение многоугольника осуществляется последовательным нанесением курсором компьютерной мыши на плоскости точек - вершин многоугольника основания. Завершается построение основания замыканием ломаной - границы основания, то есть повторным щелчком курсором компьютерной мыши по первой вершине многоугольника (рис. 1 а). Далее пользователь может выбрать (щелчком мыши) произвольную точку вне плоскости, которая при этом соединяется отрезками со всеми вершинами многоугольника основания (рис. 1 б). На получившийся каркас «натягиваются» треугольники боковой поверхности пирамиды (рис. 1 в). Они вместе с многоугольником основания ограничат в пространстве пирамиду. Далее пользователь может с помощью компьютерной мыши вращать построенную пирамиду в пространстве, осматривая ее со всех сторон (рис. 1 в, г).
- Применение в процессе создания интерактивных моделей Web-технологий позволяет, с одной стороны, создавать учебные
информационные ресурсы с простым и интуитивно понятным интерфейсом, хорошо знакомым в настоящее время подавляющему большинству учащихся. С другой стороны, такой подход решает проблему унификации цифровых образовательных ресурсов, существенно облегчая переносимость и тиражируемость создаваемых учебных материалов. Действительно, для работы с такими приложениями не требуется ничего, кроме стандартного Wcb-браузера (например, Internet Explorer), имеющегося на любом пользовательском компьютере. Еще одним важным доводом в пользу данного подхода является то, что созданные таким образом учебные материалы могут быть легко интегрированы в распределенные информационно-обучающие системы, основанные на Web-технологиях сетевого доступа пользователей. В книге для учителя даны краткие сценарии всех уроков по курсу геометрии в 9 классе. Приведем в качестве примера один из них к теме «Движения».
УРОК
ДВИЖЕНИЯ И ИХ ОБЩИЕ СВОЙСТВА
Цели урока: Познакомить учеников с понятием движения и его общими свой¬ствами.
- 1. Работа учителя со всем классом.
- Учитель говорит, что ученикам предстоит изучить два важнейших класса преобразований: движения и подобия. Движения - это те
преобразования фигур, которые сохраняют расстояния между точками. Пример для учеников: на листе бумаги отметить две точки, измерить расстояние между ними, переместить лист и снова измерить расстояние. Важность движений в том, что при движениях фигура сохраняет свою форму и все свои размеры, поскольку все геометрические величины можно выразить через расстояния. Ученики вспоминают формулы, выражающие различные величины через дайны (для площадей, для углов - тригонометрия, для объемов) и утверждения о равенстве фигур, имеющих соответственно равные линейные размеры (треугольников - по трем сторонам, прямоугольников - по их измерениям, окружностей - по радиусам).
- Далее конкретизируется общее утверждение о том, что движение сохраняет все свойства фигур! Ключевым здесь является
предложение о том, что при движении образом отрезка является отрезок. Многие фигуры конструируются из отрезков: отрезки вытягиваются в лучи, в прямые. Отрезками «заметаются» треугольники (см. рис. 2). Эта и другие динамические модели, входящие в состав инновационного учебно-методического комплекса, как уже отмечаюсь выше, выполнены на основе Flash-технологий [3]. На рис. 2 а-г представлен экранный интерфейс модели в окне Web-браузера на различных этапах работы с ней пользователя. Модель служит для иллюстрации следующего утверждения: образом треугольника при движении является равный ему треугольник. В исходном состоянии в окне модели изображён исходный треугольник ABC и точка X на стороне ВС (рис. 2 а). Вершины треугольника можно перемещать произвольно, а точку X - вдоль стороны ВС (при этом закрашивается соответствующая область треугольника). В левой части окна изображён вектор с вершиной К, задающий некоторое движение f. Точка К является активной. С ее помощью можно изменять направление этого движения. При нажатии кнопки "Движение f" точки А, В и С переводятся соответственно в точки А', В' и С' (рис. 2 б). При этом в окне модели появляется образ треугольника А'В'С', который можно произвольным образом вращать курсором мыши (рис. 2 в). Этим же движением f отрезки АХ переводятся в отрезки А'Х' заполняющие треугольник А' В' С'. Этот про¬цесс можно наблюдать в интерактивном режиме, перемещая активную точку X вдоль стороны ВС (рис. 2 г). Кнопка «Сброс» в правом нижнем углу окна возвращает модель в исходное состояние. Из треугольников составляются многоугольники, из тетраэдров - многогранники.
- Удобно для свойств, сохраняющихся для рассматриваемых преобразований, ввести термин инварианты преобразований.
Этот термин позволяет более кратко формулировать предложения о сохраняющихся свойствах.
2. Самостоятельная работа учеников.
- Ученикам предлагается угадать, какие из шести важных примеров преобразований являются движениями (доказательства правильности
их гипотез будут даны на следующих уроках), а затем нарисовать несколько пар равных (одинаковых) фигур (треугольников, квадратов, окружностей и т. п.) и движениями первую из этих фигур преобразовать во вторую. Такую работу можно выполнить и на бумаге, и с помощью компьютера.
- В рабочей тетради предлагается несколько динамических моделей преобразований, в которых можно следить за сохранением или
несохранением расстояния между точками. Ученикам предлагается практически применить определение движения и правильно классифицировать преобразования. Второй (дополнительной) частью работы с рабочей тетрадью можно сделать практическую работу по самостоятельному конструированию произвольных движений плоскости из небольшого числа базовых движений. На рис. 3 представлен интерфейс одного из заданий электронной рабочей тетради, реализованной на основе Java-технологий (подробнее с рабочей тетрадью можно познакомиться в разделе «Журнал в журнале».
- Апробация разработанных учебно-методических материалов, проведенная в ряде российских школ, показала повышение интереса
учащихся к предмету и высокую эффективность использования интерактивных компьютерных моделей.
Литература
1. А.Д. Александров, Вернер Алексей Леонидович, доктор физ.-мат. наук, профессор кафедры геометрии А.Д. Александров, A.Л. Вернер, В.И. Рыжик. Геометрия, 9. Мирос, М„ 1997.
2. А.Л. Вернер, В.И. Рыжик, Т.Г. Ходот. Геометрия, 9. Просвещение, М., 2001.
3. О.Д. Андреев, A.J1. Вернер, К.А. Ляпцев, А.Б. Никитин, И.А. Цикин. Интерактивные Flash- модели в школьном курсе геометрии // Компьютерные инструменты в образовании, 2006, № 5, С. 27-31.РГПУ им. А.И.Герцена,