Семинар ДООМ: Урок по теме « Теорема Пифагора».
Проба (обсуждение | вклад) |
Проба (обсуждение | вклад) |
||
| (не показаны 11 промежуточных версий 1 участника) | |||
| Строка 47: | Строка 47: | ||
'''III. Объяснение нового материала.''' | '''III. Объяснение нового материала.''' | ||
| − | 1) Задача. Найти длину лестницы, приставленной к дому, если один её конец находится на расстоянии 3 м от дома, а другой находится на стыке стены и крыши. | + | 1) Задача. Найти длину лестницы,[[Изображение:Lectn.jpg|thumb|left| Длину лестницы мы сможем найти после изучения теоремы Пифагора]], |
| + | приставленной к дому, если один её конец находится на расстоянии 3 м от дома, | ||
| + | |||
| + | а другой находится на стыке стены и крыши. | ||
| + | |||
Высота дома 4 м. | Высота дома 4 м. | ||
| − | [[Изображение: | + | |
| + | |||
| + | '''2) О теореме Пифагора.''' Теорема Пифагора – одна из самых главных теорем геометрии. Значение её состоит в том, что из неё или с её помощью можно вывести большинство теорем геометрии и решить множество задач. | ||
| + | |||
| + | '''3) Формулировка и доказательство теоремы Пифагора.''' | ||
| + | |||
| + | '''Теорема:''' В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов. | ||
| + | |||
| + | '''Доказательство:''' | ||
| + | |||
| + | Рассмотрим прямоугольный треугольник с катетами а, b и гипотенузой с. | ||
| + | |||
| + | Докажем, что с² = а² + b² | ||
| + | [[Изображение:Dokazat.jpg|right]] | ||
| + | Достроим треугольник до квадрата со стороной a + b. | ||
| + | Площадь S этого квадрата равна (а + b)². | ||
| + | |||
| + | С другой стороны, этот квадрат составлен из четырёх равных прямоугольных треугольников, | ||
| + | площадь каждого из которых равна ½ab , и квадрата со стороной с, | ||
| + | |||
| + | поэтому S = 4 ∙ ½ab + c² = 2ab +c² | ||
| + | |||
| + | Таким образом, (a + b)² = 2ab + c², Откуда c² = a² + b² | ||
| + | |||
| + | '''Теорема доказана.''' | ||
| + | |||
| + | |||
| + | '''4) Стихотворная формулировка теоремы Пифагора.''' | ||
| + | |||
| + | |||
| + | Если дан нам треугольник | ||
| + | И при том с прямым углом, | ||
| + | То квадрат гипотенузы | ||
| + | Мы всегда легко найдём: | ||
| + | Катеты в квадрат возводим, | ||
| + | Сумму степеней находим- | ||
| + | И таким простым путём | ||
| + | К результату мы придём. | ||
| + | '''5) Устно:''' | ||
| + | Вернемся к задаче о длине лестницы. | ||
| + | AB²= AC²+BC²= 3²+4²=9+16=25 | ||
| + | AB = =5(м). | ||
| + | Ответ: длина лестницы 5 метров. | ||
| + | |||
| + | '''6) Исторический материал.''' | ||
| + | |||
| + | Существует легенда о том, что в честь своего открытия Пифагор принес в жертву быка или даже 100 быков. Это послужило поводом для юмора в рассказах писателей и в стихах поэтов. Немецкий писатель -романист А. Шамиссо написал следующие стихи: | ||
| + | Пребудет вечной истина, как скоро | ||
| + | Её познает слабый человек! | ||
| + | И ныне теорема Пифагора | ||
| + | Верна, как и в его далёкий век. | ||
| + | Обильно было жертвоприношенье | ||
| + | Богам от Пифагора. Сто быков | ||
| + | Он отдал на закланье и сожженье | ||
| + | За света луч, пришедший с облаков. | ||
| + | Поэтому всегда с тех самых пор, | ||
| + | Чуть истина рождается на свет, | ||
| + | Быки ревут, её потчуя, вслед. | ||
| + | Они не в силах свету помешать, | ||
| + | А могут лишь, закрыв глаза, дрожать | ||
| + | От страха, что вселил в них Пифагор. | ||
| + | |||
| + | Доказательство теоремы Пифагора считалось в кругах учащихся средних веков очень трудным и называлось иногда ослиный мост ( т.к. для слабых учеников эта теорема была вроде непроходимого моста) или бегство убогих, т.к. некоторые слабые «убогие» ученики бежали от геометрии. | ||
| + | В связи с чертежами, сопровождавшими доказательство теоремы Пифагора, учащиеся также называли теорему «ветряной мельницей», составляли стишки вроде: '''«Пифагоровы штаны во все стороны равны».''' | ||
| + | [[Изображение:Cheliu.jpg]] | ||
| + | |||
| + | У математиков арабского востока теорема получила название '''«теорема невесты».''' Чертёж к теореме похож на пчелу, бабочку, что по-гречески – нимфа. Также в то время называли молодых женщин, невест. | ||
| + | Для наших учеников доказательство теоремы Пифагора не является непроходимым мостом. | ||
| + | |||
| + | '''7) Древнекитайское доказательство теоремы Пифагора(ученик):''' | ||
| + | |||
| + | На древнекитайском чертеже четыре равных прямоугольных треугольника с катетами а, b и гипотенузой с уложены так, что их внешний контур образует квадрат со стороной (a+b), а внутренний -квадрат со стороной с, построенный на гипотенузе. | ||
| + | Если квадрат со стороной с вырезать, а оставшиеся четыре затушёванных треугольника уложить в два прямоугольника, то ясно, что образовавшаяся пустота, с одной стороны, равна с², с другой- a²+b², т.е. с²=а²+ b² . Теорема доказана. | ||
| + | [[Изображение:Vvvava.jpg]] | ||
| + | |||
| + | '''8)Практическая работа:'''Начертите прямой угол, отложите на его сторонах катеты 6 м и 8 м (масштаб 1 клетка-1м). | ||
| + | Получим гипотенузу равную ….(10 м). Достройте на катетах и гипотенузе квадраты. | ||
| + | Найдите S=S1 +S2 (100=36+64, т.е. 10²=6²+8²) | ||
| + | |||
| + | '''IV. Закрепление. Решение задач.''' | ||
| + | |||
| + | '''1)Египетская задача.''' На глубине 12 футов растёт лотос с 13-футовым стеблем. Определите, на какое расстояние цветок может отклониться от вертикали, проходящей через точку крепления стебля ко дну? ''(5 метров).'' | ||
| + | |||
| + | '''2)Задача индийского математика XII века Бхаскары.''' | ||
| + | <br> «На берегу реки рос тополь одинокий. | ||
| + | <br>Вдруг ветра порыв его ствол надломил. | ||
| + | <br>Бедный тополь упал. И угол прямой | ||
| + | <br>С теченьем реки его ствол составлял. | ||
| + | <br>Запомни теперь, что в этом месте река | ||
| + | <br>В четыре лишь фута была широка. | ||
| + | <br>Верхушка склонилась у края реки. | ||
| + | <br>Осталось три фута всего от ствола. | ||
| + | <br>Прошу тебя, скоро теперь мне скажи: | ||
| + | <br>У тополя как велика высота?» ''(8 футов)'' | ||
| + | |||
| + | '''V.Задание на дом. Теорема Пифагора, №483(в,г), 488(а,б)''' | ||
| + | |||
| + | '''VI. Итоги урока. Оценка учащихся.''' | ||
| + | В конце урока каждый ученик получает отдельные афоризмы Пифагора. | ||
| + | |||
| + | В школе Пифагора большое значение придавалось духовному развитию учеников. Существовал моральный кодекс''' « Золотые стихи»,''' который содержал правила поведения, основные принципы жизни. Вот некоторые из них: | ||
| + | |||
| + | 1) Статую красит вид, а человека-деяния его. | ||
| + | |||
| + | 2) Есть две поры наиболее подходящие для размышлений: когда идёшь ко сну и когда пробуждаешься от сна. В это время требуй от себя отчёта. Оцени, что сделано и что предстоит сделать. | ||
| + | |||
| + | 3) Не гоняйся за счастьем: оно всегда находится в тебе самом. | ||
| + | |||
| + | 4) Прежде чем станешь говорить, дай время созреть твоей мысли под твоим языком. | ||
| + | |||
| + | 5) Измеряй свои желания, взвешивай свои мысли, исчисляй свои слова. | ||
| + | |||
| + | '''''Эти общечеловеческие ценности актуальны и по сей день.''''' | ||
| + | |||
| + | |||
| + | |||
| + | [[Категория:Проект ДООМ 2009-2010]]. | ||
Текущая версия на 23:19, 5 декабря 2009
Урок в 8 классе по теме « Теорема Пифагора».
Автор Рыскалкина Наталия Васильевна
Цели урока:
1. Научить доказывать теорему Пифагора.
2. Научить применять теорему Пифагора к решению задач.
3. Развитие интереса к математике через ознакомление с историческим материалом.
Ход урока.
I. Вступительное слово учителя.
Да, путь познания не гладок.
Но знаем мы со школьных лет,
Загадок больше, чем разгадок,
И поискам предела нет!
На радужной узрел я оболочке
Бегущие квадратики, кружочки,
Вселенной опрокинутый узор,
И вспыхнуло в мелькании сквозь строчки
Пылающее имя – Пифагор!
Учитель формулирует тему и цели урока.
II. Подготовительная работа.
-Как называют стороны прямоугольного треугольника?
-Чему равна площадь прямоугольного треугольника?
-Чему равна площадь квадрата?
-Чему равен квадрат суммы двух выражений?
III. Объяснение нового материала.
1) Задача. Найти длину лестницы,,приставленной к дому, если один её конец находится на расстоянии 3 м от дома,
а другой находится на стыке стены и крыши.
Высота дома 4 м.
2) О теореме Пифагора. Теорема Пифагора – одна из самых главных теорем геометрии. Значение её состоит в том, что из неё или с её помощью можно вывести большинство теорем геометрии и решить множество задач.
3) Формулировка и доказательство теоремы Пифагора.
Теорема: В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
Доказательство:
Рассмотрим прямоугольный треугольник с катетами а, b и гипотенузой с.
Докажем, что с² = а² + b²
Достроим треугольник до квадрата со стороной a + b. Площадь S этого квадрата равна (а + b)².
С другой стороны, этот квадрат составлен из четырёх равных прямоугольных треугольников, площадь каждого из которых равна ½ab , и квадрата со стороной с,
поэтому S = 4 ∙ ½ab + c² = 2ab +c²
Таким образом, (a + b)² = 2ab + c², Откуда c² = a² + b²
Теорема доказана.
4) Стихотворная формулировка теоремы Пифагора.
Если дан нам треугольник
И при том с прямым углом,
То квадрат гипотенузы
Мы всегда легко найдём:
Катеты в квадрат возводим,
Сумму степеней находим-
И таким простым путём
К результату мы придём.
5) Устно:
Вернемся к задаче о длине лестницы.
AB²= AC²+BC²= 3²+4²=9+16=25
AB = =5(м).
Ответ: длина лестницы 5 метров.
6) Исторический материал.
Существует легенда о том, что в честь своего открытия Пифагор принес в жертву быка или даже 100 быков. Это послужило поводом для юмора в рассказах писателей и в стихах поэтов. Немецкий писатель -романист А. Шамиссо написал следующие стихи:
Пребудет вечной истина, как скоро
Её познает слабый человек!
И ныне теорема Пифагора
Верна, как и в его далёкий век.
Обильно было жертвоприношенье
Богам от Пифагора. Сто быков
Он отдал на закланье и сожженье
За света луч, пришедший с облаков.
Поэтому всегда с тех самых пор,
Чуть истина рождается на свет,
Быки ревут, её потчуя, вслед.
Они не в силах свету помешать,
А могут лишь, закрыв глаза, дрожать
От страха, что вселил в них Пифагор.
Доказательство теоремы Пифагора считалось в кругах учащихся средних веков очень трудным и называлось иногда ослиный мост ( т.к. для слабых учеников эта теорема была вроде непроходимого моста) или бегство убогих, т.к. некоторые слабые «убогие» ученики бежали от геометрии.
В связи с чертежами, сопровождавшими доказательство теоремы Пифагора, учащиеся также называли теорему «ветряной мельницей», составляли стишки вроде: «Пифагоровы штаны во все стороны равны».
У математиков арабского востока теорема получила название «теорема невесты». Чертёж к теореме похож на пчелу, бабочку, что по-гречески – нимфа. Также в то время называли молодых женщин, невест. Для наших учеников доказательство теоремы Пифагора не является непроходимым мостом.
7) Древнекитайское доказательство теоремы Пифагора(ученик):
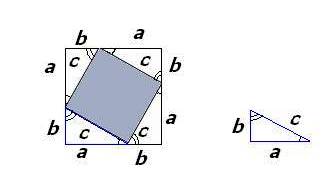
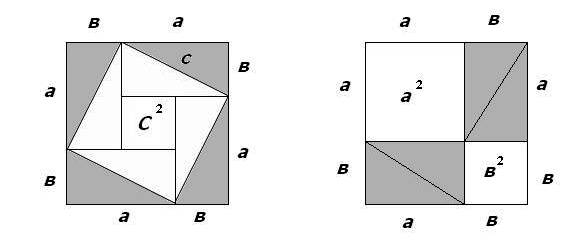
На древнекитайском чертеже четыре равных прямоугольных треугольника с катетами а, b и гипотенузой с уложены так, что их внешний контур образует квадрат со стороной (a+b), а внутренний -квадрат со стороной с, построенный на гипотенузе.
Если квадрат со стороной с вырезать, а оставшиеся четыре затушёванных треугольника уложить в два прямоугольника, то ясно, что образовавшаяся пустота, с одной стороны, равна с², с другой- a²+b², т.е. с²=а²+ b² . Теорема доказана.
8)Практическая работа:Начертите прямой угол, отложите на его сторонах катеты 6 м и 8 м (масштаб 1 клетка-1м). Получим гипотенузу равную ….(10 м). Достройте на катетах и гипотенузе квадраты. Найдите S=S1 +S2 (100=36+64, т.е. 10²=6²+8²)
IV. Закрепление. Решение задач.
1)Египетская задача. На глубине 12 футов растёт лотос с 13-футовым стеблем. Определите, на какое расстояние цветок может отклониться от вертикали, проходящей через точку крепления стебля ко дну? (5 метров).
2)Задача индийского математика XII века Бхаскары.
«На берегу реки рос тополь одинокий.
Вдруг ветра порыв его ствол надломил.
Бедный тополь упал. И угол прямой
С теченьем реки его ствол составлял.
Запомни теперь, что в этом месте река
В четыре лишь фута была широка.
Верхушка склонилась у края реки.
Осталось три фута всего от ствола.
Прошу тебя, скоро теперь мне скажи:
У тополя как велика высота?» (8 футов)
V.Задание на дом. Теорема Пифагора, №483(в,г), 488(а,б)
VI. Итоги урока. Оценка учащихся. В конце урока каждый ученик получает отдельные афоризмы Пифагора.
В школе Пифагора большое значение придавалось духовному развитию учеников. Существовал моральный кодекс « Золотые стихи», который содержал правила поведения, основные принципы жизни. Вот некоторые из них:
1) Статую красит вид, а человека-деяния его.
2) Есть две поры наиболее подходящие для размышлений: когда идёшь ко сну и когда пробуждаешься от сна. В это время требуй от себя отчёта. Оцени, что сделано и что предстоит сделать.
3) Не гоняйся за счастьем: оно всегда находится в тебе самом.
4) Прежде чем станешь говорить, дай время созреть твоей мысли под твоим языком.
5) Измеряй свои желания, взвешивай свои мысли, исчисляй свои слова.
Эти общечеловеческие ценности актуальны и по сей день..