Семинар ДООМ : Таблица смежности
| (не показаны 2 промежуточные версии 1 участника) | |||
| Строка 1: | Строка 1: | ||
Иванова Елена Андреевна, руководитель команды "Смежные вершины 025" | Иванова Елена Андреевна, руководитель команды "Смежные вершины 025" | ||
| + | |||
| + | [[Участник: Иванова Елена]] | ||
'''Занятие в 8-ом классе «Таблица смежности»''' | '''Занятие в 8-ом классе «Таблица смежности»''' | ||
| Строка 58: | Строка 60: | ||
[[Изображение:Grsm.JPG]] | [[Изображение:Grsm.JPG]] | ||
| − | Вы заметили, что наши таблицы заполнены только 0 и 1, как называются такие таблицы? | + | Вы заметили, что наши таблицы заполнены только 0 и 1, как называются такие таблицы? Двоичными матрицами. Поэтому и таблицы смежности часто называют матрицами смежности. |
| − | Но всегда ли матрица смежности подходит для описания графа (вспомните задачу о Пятачке, Вини - Пухе и т.д) ? Нет, если ребро имеет какую-то количественную характеристику, то в таблице смежности отображают уже не 0 и 1, а значение этой характеристики | + | Но всегда ли двоичная матрица смежности подходит для описания графа (вспомните задачу о Пятачке, Вини - Пухе и т.д) ? Нет, если ребро имеет какую-то количественную характеристику, то в таблице смежности отображают уже не 0 и 1, а значение этой характеристики. |
Посмотрим на '''слайд №14'''. Ответим на вопрос: | Посмотрим на '''слайд №14'''. Ответим на вопрос: | ||
| Строка 77: | Строка 79: | ||
Учащиеся по просьбе учителя пытаются сопоставить два способа представления графов, (возможны субъективные оценки, вследствие различных преобладающих форм восприятия информации), перечисляют новое для себя из изученного на уроке. | Учащиеся по просьбе учителя пытаются сопоставить два способа представления графов, (возможны субъективные оценки, вследствие различных преобладающих форм восприятия информации), перечисляют новое для себя из изученного на уроке. | ||
| − | [[Категория: Проект ДООМ]] | + | [[Категория:Проект ДООМ 2007-2008 (1 цикл)]] |
Текущая версия на 14:50, 10 января 2008
Иванова Елена Андреевна, руководитель команды "Смежные вершины 025"
Занятие в 8-ом классе «Таблица смежности»
Цели:
1. Знать понятие «таблица смежности», уметь сопоставлять разные формы представления графов, повторить понятие «матрица».
2. Развивать логическое, абстрактное мышление учащихся.
3. Воспитывать ответственное отношение к информационной деятельности.
Обеспечение: экран, проектор, презентация, раздаточный материал, доска.
ПРЕЗЕНТАЦИЮ МОЖНО СКАЧАТЬ ЗДЕСЬ Медиа:Grsm.ppt
Структура урока:
1. Организационный момент.
В начале занятия учитель предлагает учащимся совместно определить его тему. Для этого используются слайды № 2-10 презентации, первое слово темы определяется отгадыванием кроссворда, учащиеся таким образом повторяют основные определения теории графов, второе слово формируется из имен вершин, определяющих кратчайший путь между вершинами.
После отгадывания темы, учитель записывает ее на доске, а учащиеся - в тетради.
2. Объяснение нового материала.
До сих пор мы с вами говорили о геометрическом способе представления графов, т.е изображали их с помощью точек и линий. Но этот способ - не единственный. Может быть, вы попробуете придумать способ, которым можно однозначно описать граф? (если учащиеся предложат свои способы, происходит их обсуждение.
Ну а мне сегодня хочется познакомить вас с табличным способом.
Давайте посмотрим на Слайд №12. Один и тот же граф описан двумя различными способами, в таблице на пересечении столбца и строки ставится единица, если между соответствующими вершинами есть ребро и 0 если такого ребра нет.
Давайте выявим правила и закономерности построения таблиц (учащиеся, рассматривая таблицу на слайде, вносят предложения, учитель подсказывает, направляет, совместными усилиями формулируют правила):
1. Количество столбцов и строк в таблице одинаковое.
2. Количество строк и столбцов на 1 больше количества вершин (1 столбец и строка отводятся на названия вершин).
3. Если на пересечении строки и столбца с именами х и у стоит 1, то она обязательно стоит и на пересечении столбца и строки с этими именами.
4. Количество 1 в таблице всегда четно.
А теперь посмотрим на таблицу на слайде №13 и попробуем рассказать все о графе, который она описывает. (учащиеся дают характеристики, описанному графу, если что-то пропускают, учитель задает вопросы):
1. Сколько вершин у графа?
2. Сколько четных вершин, назовите их.
3. Есть ли ребро между вершинами С и Е?
4. Какова степень вершины А? и т.д
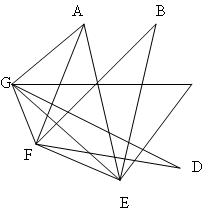
После того как таблица изучена, учитель предлагает, пользуясь таблицей построить граф в тетради. Перед этим совместно формулируется алгоритм: обозначаем вершины, соединяем ребрами согласно таблице.
В результате построения получается:
Вы заметили, что наши таблицы заполнены только 0 и 1, как называются такие таблицы? Двоичными матрицами. Поэтому и таблицы смежности часто называют матрицами смежности.
Но всегда ли двоичная матрица смежности подходит для описания графа (вспомните задачу о Пятачке, Вини - Пухе и т.д) ? Нет, если ребро имеет какую-то количественную характеристику, то в таблице смежности отображают уже не 0 и 1, а значение этой характеристики.
Посмотрим на слайд №14. Ответим на вопрос: Сколько стоит поездка по маршруту: А-С-Е, Е-В-С
Изобразим на доске соответствующий граф.
3. Первичная проверка понимания.
Работа с карточками
КАРТОЧКУ МОЖНО СКАЧАТЬ ЗДЕСЬ Медиа:Grsm.doc
4. Итог занятия
Учащиеся по просьбе учителя пытаются сопоставить два способа представления графов, (возможны субъективные оценки, вследствие различных преобладающих форм восприятия информации), перечисляют новое для себя из изученного на уроке.