Семинар ДООМ Теория Рамсея
(Новая: '''Из опыта изучения элементов теории графов на факультативных занятиях в 9 классах.''' '''Цель занятия'...) |
|||
| (не показаны 6 промежуточных версий 2 участников) | |||
| Строка 1: | Строка 1: | ||
| + | Тихомирова Лариса Николаевна 010 | ||
| + | |||
'''Из опыта изучения элементов теории графов на факультативных занятиях в 9 классах.''' | '''Из опыта изучения элементов теории графов на факультативных занятиях в 9 классах.''' | ||
| Строка 7: | Строка 9: | ||
Талантливый математик Фрэнк Пламптон Рамсей доказал, что полная неупорядоченность невозможна. Каждое достаточно большое множество чисел, точек или объектов обязательно содержит высоко упорядоченную структуру | Талантливый математик Фрэнк Пламптон Рамсей доказал, что полная неупорядоченность невозможна. Каждое достаточно большое множество чисел, точек или объектов обязательно содержит высоко упорядоченную структуру | ||
| − | + | РОНАЛЬД Л. ГРЭМ, ДЖОУЭЛ X. СПЕНСЕР | |
| + | |||
Как повествует написанный три с половиной тысячи лет назад клинописный текст, однажды древнешумерский учёный взглянул на звёздное небо и увидел льва, буйвола и скорпиона. Современный астроном скорее всего склонен описывать созвездие как временную группу звёзд, которую мы, земляне, наблюдаем с одной точки на краю обычной галактики. И всё же большинство любителей поглазеть на звёзды согласятся, что ночное небо выглядит сплошь усыпанным созвездиями, имеющими форму прямых линий, четырёхугольников и пятиугольников. Может ли так быть, что подобные геометрические фигуры порождаются какими-то неизвестными нам силами, действующими во Вселенной? | Как повествует написанный три с половиной тысячи лет назад клинописный текст, однажды древнешумерский учёный взглянул на звёздное небо и увидел льва, буйвола и скорпиона. Современный астроном скорее всего склонен описывать созвездие как временную группу звёзд, которую мы, земляне, наблюдаем с одной точки на краю обычной галактики. И всё же большинство любителей поглазеть на звёзды согласятся, что ночное небо выглядит сплошь усыпанным созвездиями, имеющими форму прямых линий, четырёхугольников и пятиугольников. Может ли так быть, что подобные геометрические фигуры порождаются какими-то неизвестными нам силами, действующими во Вселенной? | ||
Математика предлагает куда более простое объяснение. В 1928 году Фрэнк Пламптон Рамсей сделал доклад в Лондонском математическом обществе по работе «Об одной проблеме в формальной логике», в которой доказал, что такие упорядоченные конфигурации неизбежно присутствуют в любой большой структуре, будь то группа звёзд, совокупность случайно разбросанных камешков или последовательность чисел, полученных бросанием игральной кости. Если речь идёт о достаточно большом количестве звёзд, то всегда можно найти группу, которая с очень большой точностью образует какую-нибудь заданную конфигурацию: прямую линию, прямоугольник или, если уж мы заговорили о звёздах, большой ковш. Фактически теория Рамсея утверждает, что любая структура обязательно содержит упорядоченную подструктуру. Из теории Рамсея следует, что полный беспорядок невозможен. | Математика предлагает куда более простое объяснение. В 1928 году Фрэнк Пламптон Рамсей сделал доклад в Лондонском математическом обществе по работе «Об одной проблеме в формальной логике», в которой доказал, что такие упорядоченные конфигурации неизбежно присутствуют в любой большой структуре, будь то группа звёзд, совокупность случайно разбросанных камешков или последовательность чисел, полученных бросанием игральной кости. Если речь идёт о достаточно большом количестве звёзд, то всегда можно найти группу, которая с очень большой точностью образует какую-нибудь заданную конфигурацию: прямую линию, прямоугольник или, если уж мы заговорили о звёздах, большой ковш. Фактически теория Рамсея утверждает, что любая структура обязательно содержит упорядоченную подструктуру. Из теории Рамсея следует, что полный беспорядок невозможен. | ||
| − | Головоломка. | + | |
| + | ''Головоломка.'' | ||
| + | |||
Доказать, что в любой компании из шести человек найдутся трое людей либо попарно знакомых, либо попарно абсолютно незнакомых. | Доказать, что в любой компании из шести человек найдутся трое людей либо попарно знакомых, либо попарно абсолютно незнакомых. | ||
| + | |||
Мы можем решить эту головоломку многими способами. Можно перебрать все мыслимые комбинации и проверить, содержит ли каждая рассматриваемая группа трёх знакомых или трёх незнакомых людей. Но поскольку нам пришлось бы проверить 32 768 (или 215) комбинаций, то такой «метод грубой силы» не является ни практичным, ни поучительным. | Мы можем решить эту головоломку многими способами. Можно перебрать все мыслимые комбинации и проверить, содержит ли каждая рассматриваемая группа трёх знакомых или трёх незнакомых людей. Но поскольку нам пришлось бы проверить 32 768 (или 215) комбинаций, то такой «метод грубой силы» не является ни практичным, ни поучительным. | ||
Эту головоломку легко преобразовать в задачу о графах. Шесть вершин соответствуют шести людям. Соединим пару вершин, соответствующих двум знакомым людям, красной линией, а пару вершин, соответствующих двум незнакомым людям, синей линией. Теперь задача состоит в том, чтобы доказать, что, как бы мы не выбирали цвета линий, у нас неизбежно получится или красный треугольник (соответствующий тройке попарно знакомых), или синий треугольник (соответствующий тройке попарно незнакомых). | Эту головоломку легко преобразовать в задачу о графах. Шесть вершин соответствуют шести людям. Соединим пару вершин, соответствующих двум знакомым людям, красной линией, а пару вершин, соответствующих двум незнакомым людям, синей линией. Теперь задача состоит в том, чтобы доказать, что, как бы мы не выбирали цвета линий, у нас неизбежно получится или красный треугольник (соответствующий тройке попарно знакомых), или синий треугольник (соответствующий тройке попарно незнакомых). | ||
| Строка 17: | Строка 23: | ||
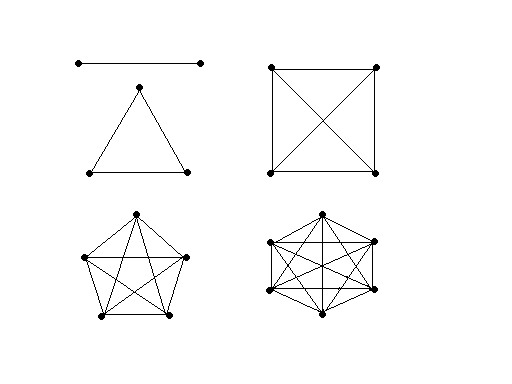
Теория графов изучает множества точек, или вершин, соединенных линиями. Если каждая из n вершин соединена линией с каждой другой вершиной, то граф называется полным графом с n вершинами и обозначается . На рисунке 1 показаны обычные способы изображения полных графов, имеющих от двух до шести вершин. | Теория графов изучает множества точек, или вершин, соединенных линиями. Если каждая из n вершин соединена линией с каждой другой вершиной, то граф называется полным графом с n вершинами и обозначается . На рисунке 1 показаны обычные способы изображения полных графов, имеющих от двух до шести вершин. | ||
| + | [[Изображение:Графы jpg.jpg]] | ||
| Строка 24: | Строка 31: | ||
| + | |||
Рис.1 | Рис.1 | ||
| − | + | ||
| + | Подграф полного графа – это какой угодно граф, содержащийся в полном графе в том смысле, что все его вершины и линии принадлежат этому полному графу. Легко видеть, что всякий полный граф является подграфом всякого полного графа с большим числом вершин. На рисунке 2 показаны четыре семейства графов: цепи, циклы, звезды и колеса. | ||
| + | |||
| + | [[Изображение:Семейства графов.jpg]] | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
Рис.2 | Рис.2 | ||
| + | |||
Рассмотрим задачу, в которой участвуют шесть карандашей различных цветов. Каждому цвету поставим в соответствие определенный тип графа, какой нам нравится. Например: | Рассмотрим задачу, в которой участвуют шесть карандашей различных цветов. Каждому цвету поставим в соответствие определенный тип графа, какой нам нравится. Например: | ||
| + | |||
1. красный-пятиугольник (5-вершинный цикл), | 1. красный-пятиугольник (5-вершинный цикл), | ||
2. оранжевый - тетраэдр, | 2. оранжевый - тетраэдр, | ||
| Строка 35: | Строка 54: | ||
5. синий – 8-вершинное колесо, | 5. синий – 8-вершинное колесо, | ||
6. фиолетовый – галстук-бабочка (два треугольника с одной общей вершиной). | 6. фиолетовый – галстук-бабочка (два треугольника с одной общей вершиной). | ||
| + | |||
Существуют ли полные графы, при любой шестицветной раскраске которых обязательно получится подграф одного из перечисленных выше типов? Другими словами, как бы мы ни раскрашивали такой полный граф шестью карандашами, мы непременно получим либо красный пятиугольник, либо оранжевый тетраэдр, либо желтую семивершинную звезду, и т.д. Теорема Рамсея утверждает, что все полученные графы, начиная с определенного конечного размера, обладают этим свойством (Каждое достаточно большое множество чисел, точек или объектов обязательно содержит высоко упорядоченную структуру). Наименьший граф из этого бесконечного семейства называется графом Рамсея для заданного множества подграфов. Число его вершин называется числом Рамсея для этого множества подграфов. | Существуют ли полные графы, при любой шестицветной раскраске которых обязательно получится подграф одного из перечисленных выше типов? Другими словами, как бы мы ни раскрашивали такой полный граф шестью карандашами, мы непременно получим либо красный пятиугольник, либо оранжевый тетраэдр, либо желтую семивершинную звезду, и т.д. Теорема Рамсея утверждает, что все полученные графы, начиная с определенного конечного размера, обладают этим свойством (Каждое достаточно большое множество чисел, точек или объектов обязательно содержит высоко упорядоченную структуру). Наименьший граф из этого бесконечного семейства называется графом Рамсея для заданного множества подграфов. Число его вершин называется числом Рамсея для этого множества подграфов. | ||
С каждым графом Рамсея связана как игра, так и головоломка. Игра в нашем примере заключается в следующем. Два игрока по очереди берут любой из шести карандашей и раскрашивают одну линию в графе Рамсея. Первый, кто закончит раскрашивание одного из заданных подграфов, считается проигравшим. Так как граф является графом Рамсея, игра не может закончиться вничью. | С каждым графом Рамсея связана как игра, так и головоломка. Игра в нашем примере заключается в следующем. Два игрока по очереди берут любой из шести карандашей и раскрашивают одну линию в графе Рамсея. Первый, кто закончит раскрашивание одного из заданных подграфов, считается проигравшим. Так как граф является графом Рамсея, игра не может закончиться вничью. | ||
Головоломка касается полного графа, имеющего на одну вершину меньше, чем граф Рамсея и состоит в нахождении раскраски этого графа, при которой не возникает ни одного из заданных подграфов. | Головоломка касается полного графа, имеющего на одну вершину меньше, чем граф Рамсея и состоит в нахождении раскраски этого графа, при которой не возникает ни одного из заданных подграфов. | ||
| − | Наиболее известная игра Рамсея (Сим) играется на полном графе из шести вершин | + | Наиболее известная игра Рамсея (Сим) играется на полном графе из шести вершин, который моделирует задачу о компании из шести человек. Число 6 есть число Рамсея для следующих двух подграфов: |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | 1. красный: треугольник , | |
| + | 2. синий: треугольник . | ||
| + | В классической теории Рамсея принято полные графы обозначать просто числами. Приведенный выше результат можно выразить компактной формулой: R(3,3)=6 Это значит, что число вершин наименьшего полного графа, который при любой двухцветной раскраске обязательно содержит одноцветный (красный или синий) треугольник, равно 6. Таким образом, если два игрока поочередно раскрашивают граф в красный и синий цвет, то один из них непременно проиграет, завершив построение одноцветного треугольника. Соответствующая головоломка состоит в том, чтобы раскрасить двумя цветами граф так, чтобы не было одноцветных треугольников (рис. 3). Решение аналогичных головоломок приведено на рис.4,5. | ||
| + | <gallery> | ||
| + | Изображение:Ramsey1.gif|Рис.3 | ||
| + | Изображение:Ramsey2.jpg|Рис.4 | ||
| + | Изображение:Ramsey3.jpg|Рис.5 | ||
| + | </gallery> | ||
| + | Специалисты по теории Рамсея стараются вычислить, сколь велико должно быть множество звёзд, чисел или каких-либо объектов, чтобы можно было гарантировать существование определённой желаемой подструктуры. На решение таких задач часто требуются десятилетия, и поддаются они только при самом изобретательном и тонком рассуждении. Пытаясь найти решения поставленной задачи, специалисты по теории Рамсея помогают тем самым инженерам в построении более совершенных сетей коммуникации и систем передачи и поиска информации. Они также открыли некоторые математические методы, которые пригодятся учёным следующего столетия. Возможно, самое важное заключается в том, что теория Рамсея исследует основополагающую структуру математики, т.е. структуру, пронизывающую всю Вселенную. | ||
| + | |||
| + | '''Литература''' | ||
| − | |||
| − | |||
| − | |||
| − | |||
1. Ronald L. Graham, Bruce L. Rothschild and Joel H. Spencer. Ramsey Theory. Second Edition. John Wiley & Sons, Inc., 1990. | 1. Ronald L. Graham, Bruce L. Rothschild and Joel H. Spencer. Ramsey Theory. Second Edition. John Wiley & Sons, Inc., 1990. | ||
| + | |||
2. М Гарднер. Рамсеевская теория графов. Квант №4, 1988г. | 2. М Гарднер. Рамсеевская теория графов. Квант №4, 1988г. | ||
| + | |||
| + | [[Категория:Проект ДООМ 2007-2008 (1 цикл)]] | ||
| + | |||
| + | [[Категория:Математика]] | ||
Текущая версия на 13:30, 8 июля 2009
Тихомирова Лариса Николаевна 010
Из опыта изучения элементов теории графов на факультативных занятиях в 9 классах.
Цель занятия – познакомить с основными понятиями теории графов Рамсея
и показать применение теории к решению головоломок и задач занимательного характера.(или история одной головоломки)
Талантливый математик Фрэнк Пламптон Рамсей доказал, что полная неупорядоченность невозможна. Каждое достаточно большое множество чисел, точек или объектов обязательно содержит высоко упорядоченную структуру
РОНАЛЬД Л. ГРЭМ, ДЖОУЭЛ X. СПЕНСЕР
Как повествует написанный три с половиной тысячи лет назад клинописный текст, однажды древнешумерский учёный взглянул на звёздное небо и увидел льва, буйвола и скорпиона. Современный астроном скорее всего склонен описывать созвездие как временную группу звёзд, которую мы, земляне, наблюдаем с одной точки на краю обычной галактики. И всё же большинство любителей поглазеть на звёзды согласятся, что ночное небо выглядит сплошь усыпанным созвездиями, имеющими форму прямых линий, четырёхугольников и пятиугольников. Может ли так быть, что подобные геометрические фигуры порождаются какими-то неизвестными нам силами, действующими во Вселенной? Математика предлагает куда более простое объяснение. В 1928 году Фрэнк Пламптон Рамсей сделал доклад в Лондонском математическом обществе по работе «Об одной проблеме в формальной логике», в которой доказал, что такие упорядоченные конфигурации неизбежно присутствуют в любой большой структуре, будь то группа звёзд, совокупность случайно разбросанных камешков или последовательность чисел, полученных бросанием игральной кости. Если речь идёт о достаточно большом количестве звёзд, то всегда можно найти группу, которая с очень большой точностью образует какую-нибудь заданную конфигурацию: прямую линию, прямоугольник или, если уж мы заговорили о звёздах, большой ковш. Фактически теория Рамсея утверждает, что любая структура обязательно содержит упорядоченную подструктуру. Из теории Рамсея следует, что полный беспорядок невозможен.
Головоломка.
Доказать, что в любой компании из шести человек найдутся трое людей либо попарно знакомых, либо попарно абсолютно незнакомых.
Мы можем решить эту головоломку многими способами. Можно перебрать все мыслимые комбинации и проверить, содержит ли каждая рассматриваемая группа трёх знакомых или трёх незнакомых людей. Но поскольку нам пришлось бы проверить 32 768 (или 215) комбинаций, то такой «метод грубой силы» не является ни практичным, ни поучительным. Эту головоломку легко преобразовать в задачу о графах. Шесть вершин соответствуют шести людям. Соединим пару вершин, соответствующих двум знакомым людям, красной линией, а пару вершин, соответствующих двум незнакомым людям, синей линией. Теперь задача состоит в том, чтобы доказать, что, как бы мы не выбирали цвета линий, у нас неизбежно получится или красный треугольник (соответствующий тройке попарно знакомых), или синий треугольник (соответствующий тройке попарно незнакомых). Теория Рамсея, имеющая дело с такими задачами, названа по имени Фрэнка Пламптона Рамсея, английского математика, философа и экономиста. Его отец, Артур С. Рамсей, был профессором математики и президентом колледжа Магдалины Кембриджского университета. В 1925 году молодой Рамсей, признанный самым лучшим студентом в области математики, окончил университет. Теория графов изучает множества точек, или вершин, соединенных линиями. Если каждая из n вершин соединена линией с каждой другой вершиной, то граф называется полным графом с n вершинами и обозначается . На рисунке 1 показаны обычные способы изображения полных графов, имеющих от двух до шести вершин.
Рис.1
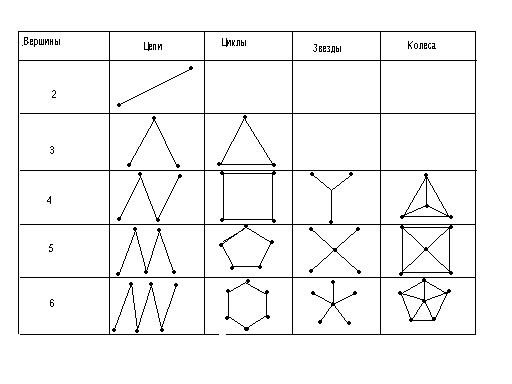
Подграф полного графа – это какой угодно граф, содержащийся в полном графе в том смысле, что все его вершины и линии принадлежат этому полному графу. Легко видеть, что всякий полный граф является подграфом всякого полного графа с большим числом вершин. На рисунке 2 показаны четыре семейства графов: цепи, циклы, звезды и колеса.
Рис.2
Рассмотрим задачу, в которой участвуют шесть карандашей различных цветов. Каждому цвету поставим в соответствие определенный тип графа, какой нам нравится. Например:
1. красный-пятиугольник (5-вершинный цикл), 2. оранжевый - тетраэдр, 3.желтый – 7-вершинная звезда, 4.зеленый – 13-вершинная цепь, 5. синий – 8-вершинное колесо, 6. фиолетовый – галстук-бабочка (два треугольника с одной общей вершиной).
Существуют ли полные графы, при любой шестицветной раскраске которых обязательно получится подграф одного из перечисленных выше типов? Другими словами, как бы мы ни раскрашивали такой полный граф шестью карандашами, мы непременно получим либо красный пятиугольник, либо оранжевый тетраэдр, либо желтую семивершинную звезду, и т.д. Теорема Рамсея утверждает, что все полученные графы, начиная с определенного конечного размера, обладают этим свойством (Каждое достаточно большое множество чисел, точек или объектов обязательно содержит высоко упорядоченную структуру). Наименьший граф из этого бесконечного семейства называется графом Рамсея для заданного множества подграфов. Число его вершин называется числом Рамсея для этого множества подграфов. С каждым графом Рамсея связана как игра, так и головоломка. Игра в нашем примере заключается в следующем. Два игрока по очереди берут любой из шести карандашей и раскрашивают одну линию в графе Рамсея. Первый, кто закончит раскрашивание одного из заданных подграфов, считается проигравшим. Так как граф является графом Рамсея, игра не может закончиться вничью. Головоломка касается полного графа, имеющего на одну вершину меньше, чем граф Рамсея и состоит в нахождении раскраски этого графа, при которой не возникает ни одного из заданных подграфов. Наиболее известная игра Рамсея (Сим) играется на полном графе из шести вершин, который моделирует задачу о компании из шести человек. Число 6 есть число Рамсея для следующих двух подграфов:
1. красный: треугольник , 2. синий: треугольник .
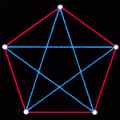
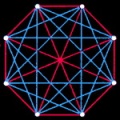
В классической теории Рамсея принято полные графы обозначать просто числами. Приведенный выше результат можно выразить компактной формулой: R(3,3)=6 Это значит, что число вершин наименьшего полного графа, который при любой двухцветной раскраске обязательно содержит одноцветный (красный или синий) треугольник, равно 6. Таким образом, если два игрока поочередно раскрашивают граф в красный и синий цвет, то один из них непременно проиграет, завершив построение одноцветного треугольника. Соответствующая головоломка состоит в том, чтобы раскрасить двумя цветами граф так, чтобы не было одноцветных треугольников (рис. 3). Решение аналогичных головоломок приведено на рис.4,5.
Специалисты по теории Рамсея стараются вычислить, сколь велико должно быть множество звёзд, чисел или каких-либо объектов, чтобы можно было гарантировать существование определённой желаемой подструктуры. На решение таких задач часто требуются десятилетия, и поддаются они только при самом изобретательном и тонком рассуждении. Пытаясь найти решения поставленной задачи, специалисты по теории Рамсея помогают тем самым инженерам в построении более совершенных сетей коммуникации и систем передачи и поиска информации. Они также открыли некоторые математические методы, которые пригодятся учёным следующего столетия. Возможно, самое важное заключается в том, что теория Рамсея исследует основополагающую структуру математики, т.е. структуру, пронизывающую всю Вселенную.
Литература
1. Ronald L. Graham, Bruce L. Rothschild and Joel H. Spencer. Ramsey Theory. Second Edition. John Wiley & Sons, Inc., 1990.
2. М Гарднер. Рамсеевская теория графов. Квант №4, 1988г.