Семинар ДООМ: Метод графов в задачах "Кенгуру"
(Новая: Метод графов в задачах «Кенгуру» Рано или поздно всякая правильная математи-ческая идея находила пр...) |
|||
| (не показаны 2 промежуточные версии 1 участника) | |||
| Строка 1: | Строка 1: | ||
Метод графов в задачах «Кенгуру» | Метод графов в задачах «Кенгуру» | ||
| − | Рано или поздно всякая правильная | + | Рано или поздно всякая правильная математическая идея находила применение в том или ином деле. |
| − | Алексей Николаевич Крылов | + | (Алексей Николаевич Крылов) |
| − | Кто сегодня не играет в «Кенгуру». Большинство учителей математики | + | Кто сегодня не играет в «Кенгуру». Большинство учителей математики удивленно пожмет плечами: «Таких нет». Потому что, на сегодняшний день, это самая массовая и хорошо организованная в международном масштабе математическая олимпиада. |
| − | Игра-конкурс «Кенгуру-математика для всех» возник в Австрии. Идея этого конкурса принадлежит известному математику и педагогу Питеру Холлорану. | + | Игра-конкурс «Кенгуру-математика для всех» возник в Австрии. Идея этого конкурса принадлежит известному математику и педагогу Питеру Холлорану. Целью конкурса является - привитие самому широкому кругу учащихся интереса к математике. Удивительный мир математики предстает перед участниками конкурса-игры с самой привлекательной стороны: со стороны мира занимательных, нестан-дартных задач; мира, который наполнен добрыми персонажами детских сказок; мира, в котором все просто и очень интересно и совсем не страшно сделать первый шаг, а потом второй, третий… |
Все это замечательно, однако мудрость гласит: « Хорош тот экспромт, который как следует подготовлен». Другими словами учитель математики должен готовить своих воспитанников к участию в олимпиаде. | Все это замечательно, однако мудрость гласит: « Хорош тот экспромт, который как следует подготовлен». Другими словами учитель математики должен готовить своих воспитанников к участию в олимпиаде. | ||
| − | В текстах «Кенгуру» за последние годы встречается достаточное количество задач, которые решаются методом графов. Любой ребенок, решающий задачу, | + | В текстах «Кенгуру» за последние годы встречается достаточное количество задач, которые решаются методом графов. Любой ребенок, решающий задачу, непроизвольно пытается изобразить условие в виде схемы, некоторого рисунка. И это понятно, визуализация условия упрощает поиск решения, поэтому метод графов воспринимается детьми естественным образом. |
| − | Теоретическая и практическая основа по теории графов, предложенная в | + | Теоретическая и практическая основа по теории графов, предложенная в дистанционной обучающей олимпиаде по математике ДООМ, позволяет учащимся даже без помощи учителя освоить основные понятия этой теории и научиться применять их в решении задач, и что самое главное, сделать самые первые шаги к самообучению с помощью Интернет-технологий. |
| − | Если знания получены и не нашли дальнейшего применения – это плохо. Олимпиада ДООМ заканчивается, а расставаться не хочется. На носу «Кенгуру». Давайте посмотрим, какие задачи «Кенгуру» решаются методом графов. Такое | + | Если знания получены и не нашли дальнейшего применения – это плохо. Олимпиада ДООМ заканчивается, а расставаться не хочется. На носу «Кенгуру». Давайте посмотрим, какие задачи «Кенгуру» решаются методом графов. Такое задание было предложено Парной Даше, ученице 7а класса, капитану команды Новички 019. Результат ее поисков представлен участникам ДООМа на блиц-турнире. |
Попытаюсь сделать несложную классификацию задач на графы в «Кенгуру». | Попытаюсь сделать несложную классификацию задач на графы в «Кенгуру». | ||
| Строка 15: | Строка 15: | ||
1. Задачи на перебор вариантов, комбинаторные. Хорошо решаются с помощью деревьев. Например: | 1. Задачи на перебор вариантов, комбинаторные. Хорошо решаются с помощью деревьев. Например: | ||
| − | Задача.У Саши есть 4 карточки с цифрами 1,2,3 и 4.Он составляет из них трехзначные | + | Задача.У Саши есть 4 карточки с цифрами 1,2,3 и 4.Он составляет из них трехзначные числа. Сколько различных чисел, делящихся на 6, он может получить? |
(А) 6 (В) 4 (С) 2 (D) 8 (E) 10 | (А) 6 (В) 4 (С) 2 (D) 8 (E) 10 | ||
| Строка 21: | Строка 21: | ||
Построить дерево вариантов здесь не сложно, остается из полученных трехзначных чисел отобрать те, которые делятся на 6. | Построить дерево вариантов здесь не сложно, остается из полученных трехзначных чисел отобрать те, которые делятся на 6. | ||
| − | Задача. Четыре человека сидят на скамейке. В некоторый момент они встают со скамьи, а затем садятся снова | + | Задача. Четыре человека сидят на скамейке. В некоторый момент они встают со скамьи, а затем садятся снова. Сколькими способами можно сесть так, чтобы ни один из них не сидел на ранее занятом месте. |
(А) 24 (В) 9 (С) 1 (D) 4 (E) 12 | (А) 24 (В) 9 (С) 1 (D) 4 (E) 12 | ||
| Строка 33: | Строка 33: | ||
[[Изображение:Граф 2.jpg]] | [[Изображение:Граф 2.jpg]] | ||
| − | Анализ схемы позволяет наметить пути возможного движения и сосчитать их | + | Анализ схемы позволяет наметить пути возможного движения и сосчитать их количество. |
1) А-В-Д 3*4=12; | 1) А-В-Д 3*4=12; | ||
| Строка 51: | Строка 51: | ||
(А) 18; (В) 4; (С) 5; (Д) 6; (Е) 7. | (А) 18; (В) 4; (С) 5; (Д) 6; (Е) 7. | ||
| − | 5. Логические задачи, задачи «кто есть кто», задачи на переливание и | + | 5. Логические задачи, задачи «кто есть кто», задачи на переливание и взвешивание. |
Задача. Когда идет дождь, кошка сидит в комнате или в подвале. Когда кошка в комнате, мышка сидит в норке, а сыр лежит в холодильнике. Если сыр на столе, а кошка - в подвале, то мышка – в комнате. Сейчас идет дождь, а сыр лежит на столе. Тогда обязательно | Задача. Когда идет дождь, кошка сидит в комнате или в подвале. Когда кошка в комнате, мышка сидит в норке, а сыр лежит в холодильнике. Если сыр на столе, а кошка - в подвале, то мышка – в комнате. Сейчас идет дождь, а сыр лежит на столе. Тогда обязательно | ||
| Строка 61: | Строка 61: | ||
(E) такая ситуация не возможна. | (E) такая ситуация не возможна. | ||
| − | Задача. Старый гном разложил свои сокровища в 3 разноцветных сундука, стоящих у стены: в один – драгоценные камни, в другой - золотые монеты, а в третий – | + | Задача. Старый гном разложил свои сокровища в 3 разноцветных сундука, стоящих у стены: в один – драгоценные камни, в другой - золотые монеты, а в третий – магические книги. Он помнит, что |
- красный сундук, правее, чем драгоценные камни; | - красный сундук, правее, чем драгоценные камни; | ||
- магические книги правее, чем красный сундук. | - магические книги правее, чем красный сундук. | ||
| − | В каком сундуке лежат магические книги, если зеленый сундук стоит левее, чем | + | В каком сундуке лежат магические книги, если зеленый сундук стоит левее, чем синий? |
(А) в синем; | (А) в синем; | ||
| Строка 82: | Строка 82: | ||
6. Задачи «Начертить фигуру одним росчерком пера. | 6. Задачи «Начертить фигуру одним росчерком пера. | ||
| − | Задача. Петя хочет нарисовать кенгуру, не отрывая карандаш от бумаги и не | + | Задача. Петя хочет нарисовать кенгуру, не отрывая карандаш от бумаги и не проводя по одной линии дважды. С какой точки он должен начать? |
[[Изображение:граф 3.jpg]] | [[Изображение:граф 3.jpg]] | ||
| Строка 88: | Строка 88: | ||
(А) А; (В) В; (С) С; (Д) Д; (Е) нет такой точки | (А) А; (В) В; (С) С; (Д) Д; (Е) нет такой точки | ||
| − | 7. Задачи, которые решаются с помощью кругов Эйлера ( Не смогли найти в текстах с 1995 по 2004, но они точно есть.) | + | 7. Задачи, которые решаются с помощью кругов Эйлера (Не смогли найти в текстах с 1995 по 2004, но они точно есть.) |
| − | Эта - простая и далеко не полная классификация задач по содержанию, которые можно решить методом графов. Можно предложить какие-нибудь другие | + | Эта - простая и далеко не полная классификация задач по содержанию, которые можно решить методом графов. Можно предложить какие-нибудь другие классификации, например по использованной теории. |
| + | [[Рыщенкова Ольга Евгеньевна]] [http://itc.tgl.ru/wiki/index.php/%D0%A3%D1%87%D0%B0%D1%81%D1%82%D0%BD%D0%B8%D0%BA:%D0%A0%D1%8B%D1%89%D0%B5%D0%BD%D0%BA%D0%BE%D0%B2%D0%B0_%D0%9E%D0%BB%D1%8C%D0%B3%D0%B0_%D0%95%D0%B2%D0%B3%D0%B5%D0%BD%D1%8C%D0%B5%D0%B2%D0%BD%D0%B0] | ||
| − | [[Категория:Проект ДООМ]] | + | |
| + | [[Категория:Проект ДООМ 2007-2008 (1 цикл)]] | ||
Текущая версия на 15:10, 10 января 2008
Метод графов в задачах «Кенгуру»
Рано или поздно всякая правильная математическая идея находила применение в том или ином деле. (Алексей Николаевич Крылов)
Кто сегодня не играет в «Кенгуру». Большинство учителей математики удивленно пожмет плечами: «Таких нет». Потому что, на сегодняшний день, это самая массовая и хорошо организованная в международном масштабе математическая олимпиада. Игра-конкурс «Кенгуру-математика для всех» возник в Австрии. Идея этого конкурса принадлежит известному математику и педагогу Питеру Холлорану. Целью конкурса является - привитие самому широкому кругу учащихся интереса к математике. Удивительный мир математики предстает перед участниками конкурса-игры с самой привлекательной стороны: со стороны мира занимательных, нестан-дартных задач; мира, который наполнен добрыми персонажами детских сказок; мира, в котором все просто и очень интересно и совсем не страшно сделать первый шаг, а потом второй, третий… Все это замечательно, однако мудрость гласит: « Хорош тот экспромт, который как следует подготовлен». Другими словами учитель математики должен готовить своих воспитанников к участию в олимпиаде. В текстах «Кенгуру» за последние годы встречается достаточное количество задач, которые решаются методом графов. Любой ребенок, решающий задачу, непроизвольно пытается изобразить условие в виде схемы, некоторого рисунка. И это понятно, визуализация условия упрощает поиск решения, поэтому метод графов воспринимается детьми естественным образом. Теоретическая и практическая основа по теории графов, предложенная в дистанционной обучающей олимпиаде по математике ДООМ, позволяет учащимся даже без помощи учителя освоить основные понятия этой теории и научиться применять их в решении задач, и что самое главное, сделать самые первые шаги к самообучению с помощью Интернет-технологий. Если знания получены и не нашли дальнейшего применения – это плохо. Олимпиада ДООМ заканчивается, а расставаться не хочется. На носу «Кенгуру». Давайте посмотрим, какие задачи «Кенгуру» решаются методом графов. Такое задание было предложено Парной Даше, ученице 7а класса, капитану команды Новички 019. Результат ее поисков представлен участникам ДООМа на блиц-турнире.
Попытаюсь сделать несложную классификацию задач на графы в «Кенгуру».
1. Задачи на перебор вариантов, комбинаторные. Хорошо решаются с помощью деревьев. Например:
Задача.У Саши есть 4 карточки с цифрами 1,2,3 и 4.Он составляет из них трехзначные числа. Сколько различных чисел, делящихся на 6, он может получить?
(А) 6 (В) 4 (С) 2 (D) 8 (E) 10
Построить дерево вариантов здесь не сложно, остается из полученных трехзначных чисел отобрать те, которые делятся на 6.
Задача. Четыре человека сидят на скамейке. В некоторый момент они встают со скамьи, а затем садятся снова. Сколькими способами можно сесть так, чтобы ни один из них не сидел на ранее занятом месте.
(А) 24 (В) 9 (С) 1 (D) 4 (E) 12
2. Задачи на пересчет количества путей. Хорошо решаются с помощью схемы маршрутов. Например:
(А) 13 (В) 33 (С) 42 (D) 26 (E) 40
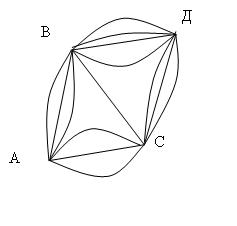
Задача. Сколько путей, идущих по стрелкам, ведут из А в D?
Анализ схемы позволяет наметить пути возможного движения и сосчитать их количество.
1) А-В-Д 3*4=12;
2) А-В-С-Д 3*1*3=9;
3) А-С-Д 3*3=9;
4) А-С-В-Д 3*1*4=12
Итого 12+9+9+12= 42
3. Задачи на оптимизацию (самый короткий маршрут, самый удобный путь, самое меньшее время, наименьшее количество рабочих дней и т.д)
Задача. Во дворе бегают 14 кошек и котят. Каждая кошка-мама вывела на прогулку не меньше двух своих котят. Каким может быть наибольшее количество кошек – мам.
(А) 18; (В) 4; (С) 5; (Д) 6; (Е) 7.
5. Логические задачи, задачи «кто есть кто», задачи на переливание и взвешивание.
Задача. Когда идет дождь, кошка сидит в комнате или в подвале. Когда кошка в комнате, мышка сидит в норке, а сыр лежит в холодильнике. Если сыр на столе, а кошка - в подвале, то мышка – в комнате. Сейчас идет дождь, а сыр лежит на столе. Тогда обязательно
(А) кошка в комнате; (В) мышка в норке; (С) кошка в комнате или мышка в норке; (D) кошка в подвале, а мышка в комнате; (E) такая ситуация не возможна.
Задача. Старый гном разложил свои сокровища в 3 разноцветных сундука, стоящих у стены: в один – драгоценные камни, в другой - золотые монеты, а в третий – магические книги. Он помнит, что - красный сундук, правее, чем драгоценные камни; - магические книги правее, чем красный сундук. В каком сундуке лежат магические книги, если зеленый сундук стоит левее, чем синий?
(А) в синем; (В) в зеленом; (С) в красном; (Д) нельзя определить; (Е) гном что-то запомнил неверно.
Задача. Восемь мальчиков живут на одной улице, каждый в своем доме. Андрей живет рядом с Бернардом, Генрих напротив Клавдия, Эрик рядом с Франциском, Даниэль рядом с Андреем, Франциск напротив Даниэля и рядом с Генрихом, Лех рядом с Эриком. Таким образом
(А) Клавдий живет около Франциска; (В) Генрих – напротив Андрея; (С) Эрик – напротив Бернарда; (Д) Клавдий – рядом с Даниэлем; (Е) Лех – рядом с Генрихом.
6. Задачи «Начертить фигуру одним росчерком пера.
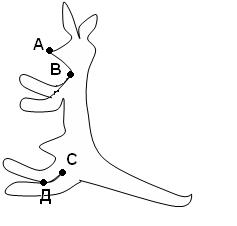
Задача. Петя хочет нарисовать кенгуру, не отрывая карандаш от бумаги и не проводя по одной линии дважды. С какой точки он должен начать?
(А) А; (В) В; (С) С; (Д) Д; (Е) нет такой точки
7. Задачи, которые решаются с помощью кругов Эйлера (Не смогли найти в текстах с 1995 по 2004, но они точно есть.)
Эта - простая и далеко не полная классификация задач по содержанию, которые можно решить методом графов. Можно предложить какие-нибудь другие классификации, например по использованной теории.