Семинар ДООМ Практические приложения подобия треугольников
(→<span style="color:#008B8B">Дистанционный урок по математике</span>) |
Nika (обсуждение | вклад) |
||
| (не показаны 44 промежуточные версии 2 участников) | |||
| Строка 1: | Строка 1: | ||
| + | __NOTOC__ | ||
| + | |||
== <span style="color:#008B8B">Дистанционный урок по математике</span> == | == <span style="color:#008B8B">Дистанционный урок по математике</span> == | ||
Автор: '''Сайфутдинова Елена Валерьевна''' [[Участник:Сайфутдинова Елена Валерьевна]] | Автор: '''Сайфутдинова Елена Валерьевна''' [[Участник:Сайфутдинова Елена Валерьевна]] | ||
| Строка 6: | Строка 8: | ||
Уважаемые участники методического семинара, предлагаю Вашему вниманию разработку дистанционного урока по математике по теме '''«Практические приложения подобия треугольников»''', материалы которого могут быть использованы для проведения традиционных уроков в школе. | Уважаемые участники методического семинара, предлагаю Вашему вниманию разработку дистанционного урока по математике по теме '''«Практические приложения подобия треугольников»''', материалы которого могут быть использованы для проведения традиционных уроков в школе. | ||
| − | === Преамбула === | + | === <span style="color:#008B8B">Преамбула</span> === |
«Измерь самого себя – и ты станешь настоящим геометром!» – воскликнул средневековый философ Марсилио Сичино. Измерять самих себя мы не будем, а вот измерить высоту дерева, соседнего здания или какой-нибудь исторической достопримечательности, почему бы и нет? | «Измерь самого себя – и ты станешь настоящим геометром!» – воскликнул средневековый философ Марсилио Сичино. Измерять самих себя мы не будем, а вот измерить высоту дерева, соседнего здания или какой-нибудь исторической достопримечательности, почему бы и нет? | ||
| − | === Форма проведения === | + | === <span style="color:#008B8B">Форма проведения</span> === |
веб-форум | веб-форум | ||
| − | === Продолжительность === | + | === <span style="color:#008B8B">Продолжительность</span> === |
2 дня | 2 дня | ||
| − | === Требования к учащимся === | + | === <span style="color:#008B8B">Требования к учащимся</span> === |
'''Учащиеся должны знать:''' | '''Учащиеся должны знать:''' | ||
| Строка 31: | Строка 33: | ||
применять данные понятия и признаки для решения простейших геометрических задач. | применять данные понятия и признаки для решения простейших геометрических задач. | ||
| − | === Аннотация урока === | + | === <span style="color:#008B8B">Аннотация урока</span> === |
Подобие треугольников широко используется при решении самых разных прикладных задачах, а определения и формулировки свойств, теорем, которые получены самостоятельно экспериментальным путем, всегда запоминаются лучше и основательнее. | Подобие треугольников широко используется при решении самых разных прикладных задачах, а определения и формулировки свойств, теорем, которые получены самостоятельно экспериментальным путем, всегда запоминаются лучше и основательнее. | ||
| Строка 37: | Строка 39: | ||
Кроме того, материал, связанный с подобием, позволяет увидеть и содержательно реализовать межпредметные связи с алгеброй (пропорциональность, уравнение), физикой (геометрическая оптика), историей (исторические справки о великих математиках древности). | Кроме того, материал, связанный с подобием, позволяет увидеть и содержательно реализовать межпредметные связи с алгеброй (пропорциональность, уравнение), физикой (геометрическая оптика), историей (исторические справки о великих математиках древности). | ||
| − | === Цели урока === | + | === <span style="color:#008B8B">Цели урока</span> === |
'''Личностные:''' | '''Личностные:''' | ||
| Строка 57: | Строка 59: | ||
* организация коммуникаций для демонстрации и сравнения разработок учащихся по проблеме измерения расстояний до недоступной точки. | * организация коммуникаций для демонстрации и сравнения разработок учащихся по проблеме измерения расстояний до недоступной точки. | ||
| − | === Программа === | + | === <span style="color:#008B8B">Программа</span> === |
| − | '''Учебный предмет и класс:''' Геометрия, 8- | + | '''Учебный предмет и класс:''' Геометрия, 8-9 класс. |
'''Раздел/тема:''' Подобие треугольников/ Применение подобия треугольников к доказательству теорем и решению прикладных задач. | '''Раздел/тема:''' Подобие треугольников/ Применение подобия треугольников к доказательству теорем и решению прикладных задач. | ||
| Строка 69: | Строка 71: | ||
'''Этапы урока по минутам:''' | '''Этапы урока по минутам:''' | ||
| − | * Модуль 1, Задание 1 – повторение (30 мин) | + | * Модуль 1, Задание 1 – повторение (30 мин) [http://www.docme.ru/doc/6711/modul._-1 Модуль 1] |
| − | * Задание 2, Модуль 2 – изучение нового материала (30 мин) | + | * Задание 2, Модуль 2 – изучение нового материала (30 мин) [http://www.docme.ru/doc/6712/modul._-2 Модуль 2] |
* Задание 3 – геометрический тренинг (5 мин) | * Задание 3 – геометрический тренинг (5 мин) | ||
| − | * Задание 4, Модуль 3 – решение прикладных задач (60 мин) | + | * Задание 4, Модуль 3 – решение прикладных задач (60 мин) [http://www.docme.ru/doc/6713/modul._-3 Модуль 3] |
| − | * Задание 5, Модуль 4 – дополнительная прикладная задача (30 мин) | + | * Задание 5, Модуль 4 – дополнительная прикладная задача (30 мин) [http://www.docme.ru/doc/6714/modul._-4 Модуль 4] |
* Задание 6 – итоговый контроль (20 мин) | * Задание 6 – итоговый контроль (20 мин) | ||
* Задание 7 – рефлексия (5 мин) | * Задание 7 – рефлексия (5 мин) | ||
| + | |||
| + | == <span style="color:#008B8B">Сценарий коммуникаций в форуме</span> == | ||
| + | |||
| + | Здравствуйте, дорогие ребята! Я рада приветствовать вас на дистанционном уроке «Практические приложения подобия треугольников». Понятие подобия является одним из важнейших в курсе геометрии. Нас везде окружают реальные предметы, дающие наглядное представление о подобных фигурах: географические карты, фотографии, модели автомобилей, кораблей, самолетов и т.д. Главная проблема урока: Можно ли, не используя специальных измерительных приборов, вычислить расстояние до недоступной точки? Как понятие подобия помогает решить эту проблему. По окончании урока вы научитесь применять подобие треугольников при доказательстве теорем и решении прикладных задач, а именно, определять расстояние до недоступной точки. А пока, в качестве разминки выполните Задание 1. Если у вас возникнут затруднения, то вы можете обратиться к Модулю 1. [http://www.docme.ru/doc/6711/modul._-1 Модуль 1] | ||
| + | |||
| + | |||
| + | === <span style="color:#008B8B">Задание 1 «Понятие подобия»</span> === | ||
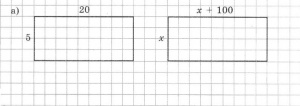
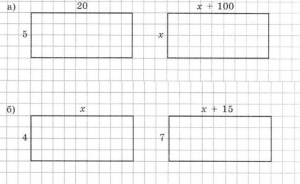
| + | [[Изображение:Картинка для урока 1.JPG|200px|thumb|right|Рисунок 1]] | ||
| + | [[Изображение:Картинка для урока 2.JPG|200px|thumb|right|Рисунок 2]] | ||
| + | а) На приведенных чертежах (Рисунок 1) изображены фигура А и фрагмент подобной ей фигуры А'. Проведи недостающие линии и дострой фигуру А'. | ||
| + | |||
| + | б) Сколько всего подобных треугольников изображено на чертежах (Рисунок 2)? | ||
| + | |||
| + | в) Методом подобия пользуются архитекторы, конструкторы, геодезисты, художники и многие другие специалисты. Перед тем как строить дом, завод или какое-нибудь другое сооружение, сначала создают его план – уменьшенное изображение будущего строения. Увеличивая фотоснимки, тоже получают подобные изображения. Составь свой расширенный список профессий которые в своей деятельности используют понятие подобия. Прокомментируй свою работу. | ||
| + | |||
| + | - Указать точные даты возникновения основных понятий математики в древнейшие времена невозможно. Еще до возникновения письменности у первобытных народов стали складываться некоторые представления о числах и фигурах. И все же за каждым математическим понятием, обозначением, доказательством «стоят» люди. Например, доказательство первых теорем приписывают Фалесу Милетскому, а понятие «координата» впервые ввел в употребление Г.В.Лейбниц. Сейчас вам предлагается выполнить «Исследовательскую работу» на предмет введения в геометрию нового понятия, и доказательство его свойств. | ||
| + | |||
| + | === <span style="color:#008B8B">Задание 2 «Исследовательская работа»</span> === | ||
| + | План работы | ||
| + | * 1 этап. Приготовь макет треугольника. Для этого вырежи из бумаги произвольный треугольник. | ||
| + | * 2 этап. Найди середины любых двух сторон твоего треугольника. Как это можно сделать, не прибегая к измерительным приборам? | ||
| + | * 3 этап. На модели проведи отрезок соединяющий середины двух сторон твоего треугольника. Какое название ты бы мог придумать такому отрезку? Что в нем особенного? Сколько таких отрезков можно построить для одного треугольника? | ||
| + | * 4 этап. Сравни длину получившегося отрезка с длиной третьей стороны треугольника. Что еще интересного ты заметил? | ||
| + | * 5 этап. По результатам 4 этапа задания сформулируй и докажи теорему о свойствах отрезка, соединяющего середины двух сторон треугольника. | ||
| + | |||
| + | После выполнения этого задания вы сравните полученные результаты с культурно-историческим аналогом описанном в модуле 2. | ||
| + | |||
| + | [http://www.docme.ru/doc/6712/modul._-2 Модуль 2] | ||
| + | |||
| + | === <span style="color:#008B8B">Задание 3 «Геометрический тренинг»</span> === | ||
| + | [[Изображение:Картинка для урока 3.JPG|200px|thumb|right|Рисунок 3]] | ||
| + | В любой области знаний, а в геометрии особенно, очень важно смотреть и видеть, замечать различные особенности геометрических фигур, делать выводы из замеченных особенностей. Эти умения, которые вместе можно назвать «геометрическим зрением», необходимо постоянно тренировать и развивать. Внимательно посмотри на рисунок 3 и среди геометрических фигур найди спрятанную звезду. Удачи! | ||
| + | |||
| + | === <span style="color:#008B8B">Задание 4 «Измерение высоты здания»</span> === | ||
| + | |||
| + | Вы никогда не задавались вопросом: как люди в глубокой древности измерили радиус Земли и высоту египетских пирамид? А можно ли самим, без специальных технических средств измерить высоту дерева, соседней «высотки» или измерить ширину реки? | ||
| + | |||
| + | «Фараона многое в тебе восхищает, Фалес; но особенно ему понравилось, как измерил ты высоту пирамиды, не приложив никакого труда и не пользуясь никаким орудием. Ты поставил посох там, где кончалась тень от пирамиды, так, что солнечный луч, касаясь их вершин, образовал два треугольника; и ты показал, что как длина одной тени относится к длине другой тени, так и высота пирамиды относится к высоте посоха» Плутарх «Пир семи мудрецов». В чем состоят затруднения решения подобных задач? Сделай чертеж и составь к нему краткий комментарий. Какой способ определения высоты пирамиды мог бы предложить ты? | ||
| + | Измерь своим оригинальным способом высоту своей школы, дома в котором ты живешь или какой-нибудь достопримечательности вашего города (населенного пункта). | ||
| + | |||
| + | Познакомьтесь, как подобную задачу в глубокой древности решил Фалес, а также познакомьтесь с другими методами решения аналогичных задач. [http://www.docme.ru/doc/6713/modul._-3 Модуль 3] | ||
| + | |||
| + | Проанализируйте свои результаты. | ||
| + | |||
| + | === <span style="color:#008B8B">Задание 5 «Радиус Земли»</span> === | ||
| + | |||
| + | Известный греческий математик, астроном и философ Эратосфен, живший в III веке до н.э., впервые в истории науки сумел измерить радиус Земли. Никаких кругосветных путешествий он для этого не совершал. Воспользовался же он следующими фактами. | ||
| + | 22 июня, в день летнего солнцестояния (когда Солнце поднимается выше всего над горизонтом) в городе Александрия Египетская, где жил Эратосфен, тень от вертикального столба была в 8 раз меньше высоты этого столба. В этот же день в городе Сиене, находившемся на 4400 стадиев (800 км) южнее, Солнце стояло в зените, и вертикальный столб не отбрасывал тени. | ||
| + | Пользуясь этими данными, определи величину радиуса Земли. | ||
| + | Попытайся все необходимые рассуждения и геометрические построения сделать самостоятельно. | ||
| + | Как еще можно было бы вычислить радиус Земли? | ||
| + | |||
| + | В случае затруднения обратись к модулю 4. [http://www.docme.ru/doc/6714/modul._-4 Модуль 4] | ||
| + | |||
| + | === <span style="color:#008B8B">Задание 6 «Итоговый тест»</span> === | ||
| + | [[Изображение:Картинка для урока 4.JPG|300px|thumb|right|Рисунок 4]] | ||
| + | [[Изображение:Картинка для урока 5.jpg|300px|thumb|right|Рисунок 5]] | ||
| + | |||
| + | Задачи для теста | ||
| + | |||
| + | # Диаметр глобуса равен 40 см; диаметр Земли – 12000 км. Определи расстояние от Новосибирска до Москвы, если на глобусе эти города разделены расстоянием 10 см. | ||
| + | # Высота Эйфелевой башни в Париже равен 300 м. Определи, какого роста человечков надо вылепить из пластилина, чтобы они были соразмерны макету высотой 150 см. Рост человека для простоты считай равным 2 м. | ||
| + | # Составь задачи по схемам на рисунках 4, 5 и реши их. | ||
| + | # Над центром круговой площадки радиусом 6 м на высоте 10 м над землей висит фонарь. Площадка окружена забором, отбрасывающим кольцевую тень шириной 4 м. Определи высоту забора. | ||
| + | # Обезьяна, рост которой равен 1 м, поднимается вверх по канату, находящемуся между | ||
| + | расположенной на уровне земли лампой и вертикальной стеной. Конец каната касается земли в 4 м от лампы и в 12 м от стены. Определи размер тени от обезьяны на стене в тот момент, когда она: а) стоит на земле; б) поднялась на высоту собственного роста; в) поднялась на два своих роста; г) поднялась на три своих роста. | ||
| + | |||
| + | === <span style="color:#008B8B">Задание 7 «Рефлексия»</span> === | ||
| + | |||
| + | Кто не слышал о загадочном Бермудском треугольнике, в котором бесследно исчезают корабли и самолеты? А ведь знакомый всем нам с детства треугольник также таит в себе немало интересного и загадочного, и вы убедились, что свойство подобия треугольников помогает решить немало практических задач.Пришло время посмотреть, как вы усвоили материал данного урока. | ||
| + | |||
| + | # Перечислите трудности, с которыми Вы столкнулись при изучении темы данной. | ||
| + | # Каким образом Вы преодолевали трудности? За счет чего? | ||
| + | # Что Вам удалось больше всего при изучении темы и почему? | ||
| + | # Что не получилось и почему? | ||
| + | |||
| + | === <span style="color:#008B8B">Домашнее задание 8 «Трактат»</span> === | ||
| + | |||
| + | Представьте, что у Вас есть возможность написать трактат будущим школьникам. В трактате опишите ваши основные достижения и результаты, дайте наставления, «советы бывалого» по изучению темы «Практические приложения подобия треугольников», попытайтесь определить способы и виды деятельности, благодаря которым Вам удалось решить проблемы и достигнуть своих результатов. Какие рекомендации и пожелания по добыче знаний Вы дадите будущим ученикам? | ||
| + | |||
| + | [[Категория:Проект ДООМ 2010-2011]] | ||
Текущая версия на 11:51, 18 января 2011
Дистанционный урок по математике
Автор: Сайфутдинова Елена Валерьевна Участник:Сайфутдинова Елена Валерьевна
Координатор команды Пифагорчики Участник:Пифагорчики ID 149
Уважаемые участники методического семинара, предлагаю Вашему вниманию разработку дистанционного урока по математике по теме «Практические приложения подобия треугольников», материалы которого могут быть использованы для проведения традиционных уроков в школе.
Преамбула
«Измерь самого себя – и ты станешь настоящим геометром!» – воскликнул средневековый философ Марсилио Сичино. Измерять самих себя мы не будем, а вот измерить высоту дерева, соседнего здания или какой-нибудь исторической достопримечательности, почему бы и нет?
Форма проведения
веб-форум
Продолжительность
2 дня
Требования к учащимся
Учащиеся должны знать:
- определение пропорциональных отрезков;
- определение подобных треугольников;
- определение подобных фигур;
- признаки подобия треугольников.
Учащиеся должны уметь:
применять данные понятия и признаки для решения простейших геометрических задач.
Аннотация урока
Подобие треугольников широко используется при решении самых разных прикладных задачах, а определения и формулировки свойств, теорем, которые получены самостоятельно экспериментальным путем, всегда запоминаются лучше и основательнее. В любой области знаний, а в геометрии особенно, очень важно смотреть и видеть, замечать различные особенности геометрических фигур, делать выводы из замеченных особенностей. Эти умения, которые вместе можно назвать «геометрическим зрением», необходимо постоянно тренировать и развивать. Кроме того, материал, связанный с подобием, позволяет увидеть и содержательно реализовать межпредметные связи с алгеброй (пропорциональность, уравнение), физикой (геометрическая оптика), историей (исторические справки о великих математиках древности).
Цели урока
Личностные:
- приобретение веры в себя, в свои потенциальные возможности;
- реализация творческих, креативных способностей личности.
Предметные:
- изучение понятия и свойства средней линии треугольника;
- развитие умений обобщать, абстрагировать и конкретизировать свойства изучаемых объектов и отношений, и применять их при решении практических задач;
- развитие геометрической зоркости.
Креативные:
- получение и обозначение новых геометрических объектов опытным путем;
- разработка и поиск новых методов решения известных задач.
Когнетивные:
- познание объектов окружающей реальности;
- изучение способов решения возникающих проблем;
- проведение практическо - исследовательской работы на местности.
Оргдеятельностные:
- овладение навыками самоорганизации учебной деятельности;
- организация коммуникаций для демонстрации и сравнения разработок учащихся по проблеме измерения расстояний до недоступной точки.
Программа
Учебный предмет и класс: Геометрия, 8-9 класс.
Раздел/тема: Подобие треугольников/ Применение подобия треугольников к доказательству теорем и решению прикладных задач.
Основная цель: Развитие навыков решения прикладных задач по теме «Подобие треугольников».
Главная проблема урока: Можно ли, не используя специальных измерительных приборов, вычислить расстояние до недоступной точки?
Круг реальных объектов действительности, предлагаемых учащимся при изучении: Высота здания, высота дерева, радиус земного шара.
Этапы урока по минутам:
- Модуль 1, Задание 1 – повторение (30 мин) Модуль 1
- Задание 2, Модуль 2 – изучение нового материала (30 мин) Модуль 2
- Задание 3 – геометрический тренинг (5 мин)
- Задание 4, Модуль 3 – решение прикладных задач (60 мин) Модуль 3
- Задание 5, Модуль 4 – дополнительная прикладная задача (30 мин) Модуль 4
- Задание 6 – итоговый контроль (20 мин)
- Задание 7 – рефлексия (5 мин)
Сценарий коммуникаций в форуме
Здравствуйте, дорогие ребята! Я рада приветствовать вас на дистанционном уроке «Практические приложения подобия треугольников». Понятие подобия является одним из важнейших в курсе геометрии. Нас везде окружают реальные предметы, дающие наглядное представление о подобных фигурах: географические карты, фотографии, модели автомобилей, кораблей, самолетов и т.д. Главная проблема урока: Можно ли, не используя специальных измерительных приборов, вычислить расстояние до недоступной точки? Как понятие подобия помогает решить эту проблему. По окончании урока вы научитесь применять подобие треугольников при доказательстве теорем и решении прикладных задач, а именно, определять расстояние до недоступной точки. А пока, в качестве разминки выполните Задание 1. Если у вас возникнут затруднения, то вы можете обратиться к Модулю 1. Модуль 1
Задание 1 «Понятие подобия»
а) На приведенных чертежах (Рисунок 1) изображены фигура А и фрагмент подобной ей фигуры А'. Проведи недостающие линии и дострой фигуру А'.
б) Сколько всего подобных треугольников изображено на чертежах (Рисунок 2)?
в) Методом подобия пользуются архитекторы, конструкторы, геодезисты, художники и многие другие специалисты. Перед тем как строить дом, завод или какое-нибудь другое сооружение, сначала создают его план – уменьшенное изображение будущего строения. Увеличивая фотоснимки, тоже получают подобные изображения. Составь свой расширенный список профессий которые в своей деятельности используют понятие подобия. Прокомментируй свою работу.
- Указать точные даты возникновения основных понятий математики в древнейшие времена невозможно. Еще до возникновения письменности у первобытных народов стали складываться некоторые представления о числах и фигурах. И все же за каждым математическим понятием, обозначением, доказательством «стоят» люди. Например, доказательство первых теорем приписывают Фалесу Милетскому, а понятие «координата» впервые ввел в употребление Г.В.Лейбниц. Сейчас вам предлагается выполнить «Исследовательскую работу» на предмет введения в геометрию нового понятия, и доказательство его свойств.
Задание 2 «Исследовательская работа»
План работы
- 1 этап. Приготовь макет треугольника. Для этого вырежи из бумаги произвольный треугольник.
- 2 этап. Найди середины любых двух сторон твоего треугольника. Как это можно сделать, не прибегая к измерительным приборам?
- 3 этап. На модели проведи отрезок соединяющий середины двух сторон твоего треугольника. Какое название ты бы мог придумать такому отрезку? Что в нем особенного? Сколько таких отрезков можно построить для одного треугольника?
- 4 этап. Сравни длину получившегося отрезка с длиной третьей стороны треугольника. Что еще интересного ты заметил?
- 5 этап. По результатам 4 этапа задания сформулируй и докажи теорему о свойствах отрезка, соединяющего середины двух сторон треугольника.
После выполнения этого задания вы сравните полученные результаты с культурно-историческим аналогом описанном в модуле 2.
Задание 3 «Геометрический тренинг»
В любой области знаний, а в геометрии особенно, очень важно смотреть и видеть, замечать различные особенности геометрических фигур, делать выводы из замеченных особенностей. Эти умения, которые вместе можно назвать «геометрическим зрением», необходимо постоянно тренировать и развивать. Внимательно посмотри на рисунок 3 и среди геометрических фигур найди спрятанную звезду. Удачи!
Задание 4 «Измерение высоты здания»
Вы никогда не задавались вопросом: как люди в глубокой древности измерили радиус Земли и высоту египетских пирамид? А можно ли самим, без специальных технических средств измерить высоту дерева, соседней «высотки» или измерить ширину реки?
«Фараона многое в тебе восхищает, Фалес; но особенно ему понравилось, как измерил ты высоту пирамиды, не приложив никакого труда и не пользуясь никаким орудием. Ты поставил посох там, где кончалась тень от пирамиды, так, что солнечный луч, касаясь их вершин, образовал два треугольника; и ты показал, что как длина одной тени относится к длине другой тени, так и высота пирамиды относится к высоте посоха» Плутарх «Пир семи мудрецов». В чем состоят затруднения решения подобных задач? Сделай чертеж и составь к нему краткий комментарий. Какой способ определения высоты пирамиды мог бы предложить ты? Измерь своим оригинальным способом высоту своей школы, дома в котором ты живешь или какой-нибудь достопримечательности вашего города (населенного пункта).
Познакомьтесь, как подобную задачу в глубокой древности решил Фалес, а также познакомьтесь с другими методами решения аналогичных задач. Модуль 3
Проанализируйте свои результаты.
Задание 5 «Радиус Земли»
Известный греческий математик, астроном и философ Эратосфен, живший в III веке до н.э., впервые в истории науки сумел измерить радиус Земли. Никаких кругосветных путешествий он для этого не совершал. Воспользовался же он следующими фактами. 22 июня, в день летнего солнцестояния (когда Солнце поднимается выше всего над горизонтом) в городе Александрия Египетская, где жил Эратосфен, тень от вертикального столба была в 8 раз меньше высоты этого столба. В этот же день в городе Сиене, находившемся на 4400 стадиев (800 км) южнее, Солнце стояло в зените, и вертикальный столб не отбрасывал тени. Пользуясь этими данными, определи величину радиуса Земли. Попытайся все необходимые рассуждения и геометрические построения сделать самостоятельно. Как еще можно было бы вычислить радиус Земли?
В случае затруднения обратись к модулю 4. Модуль 4
Задание 6 «Итоговый тест»
Задачи для теста
- Диаметр глобуса равен 40 см; диаметр Земли – 12000 км. Определи расстояние от Новосибирска до Москвы, если на глобусе эти города разделены расстоянием 10 см.
- Высота Эйфелевой башни в Париже равен 300 м. Определи, какого роста человечков надо вылепить из пластилина, чтобы они были соразмерны макету высотой 150 см. Рост человека для простоты считай равным 2 м.
- Составь задачи по схемам на рисунках 4, 5 и реши их.
- Над центром круговой площадки радиусом 6 м на высоте 10 м над землей висит фонарь. Площадка окружена забором, отбрасывающим кольцевую тень шириной 4 м. Определи высоту забора.
- Обезьяна, рост которой равен 1 м, поднимается вверх по канату, находящемуся между
расположенной на уровне земли лампой и вертикальной стеной. Конец каната касается земли в 4 м от лампы и в 12 м от стены. Определи размер тени от обезьяны на стене в тот момент, когда она: а) стоит на земле; б) поднялась на высоту собственного роста; в) поднялась на два своих роста; г) поднялась на три своих роста.
Задание 7 «Рефлексия»
Кто не слышал о загадочном Бермудском треугольнике, в котором бесследно исчезают корабли и самолеты? А ведь знакомый всем нам с детства треугольник также таит в себе немало интересного и загадочного, и вы убедились, что свойство подобия треугольников помогает решить немало практических задач.Пришло время посмотреть, как вы усвоили материал данного урока.
- Перечислите трудности, с которыми Вы столкнулись при изучении темы данной.
- Каким образом Вы преодолевали трудности? За счет чего?
- Что Вам удалось больше всего при изучении темы и почему?
- Что не получилось и почему?
Домашнее задание 8 «Трактат»
Представьте, что у Вас есть возможность написать трактат будущим школьникам. В трактате опишите ваши основные достижения и результаты, дайте наставления, «советы бывалого» по изучению темы «Практические приложения подобия треугольников», попытайтесь определить способы и виды деятельности, благодаря которым Вам удалось решить проблемы и достигнуть своих результатов. Какие рекомендации и пожелания по добыче знаний Вы дадите будущим ученикам?