Конкурсный тур
| (не показаны 12 промежуточных версий 1 участника) | |||
| Строка 1: | Строка 1: | ||
| + | <div style="background-color:#F0FFFF "> | ||
| + | |||
'''Задача 1.''' | '''Задача 1.''' | ||
| Строка 15: | Строка 17: | ||
''Решение'' | ''Решение'' | ||
| + | Так как Валя была в белых туфлях, а у Нины ни туфли ни платья не были красными, остается Тамара у которой туфли красные. А мы знаем, что у Тамары туфли и платье одного цвета – красные. Значит у Вали голубое платье и белые туфли (так как у двух других платья и туфли ни совпали). Остается у Лиды беле платье и голубые туфли | ||
Тамара красное платье и туфли, Лида белое платье и голубые туфли, Валя голубое платье и белые туфли, | Тамара красное платье и туфли, Лида белое платье и голубые туфли, Валя голубое платье и белые туфли, | ||
| Строка 26: | Строка 29: | ||
Из города А в город В можно добраться 6 дорогами, из города Б в город В 4 получаем 6*4=24 способами. Кроме того в город В можно добраться из А через город Г 2*2=4 способа. Складываем 24+4 = 28 дорог. | Из города А в город В можно добраться 6 дорогами, из города Б в город В 4 получаем 6*4=24 способами. Кроме того в город В можно добраться из А через город Г 2*2=4 способа. Складываем 24+4 = 28 дорог. | ||
| − | '''Задача | + | '''Задача 4.''' |
Антон, Борис и Виктор купили 3 билета на футбол на 1-е, 2-е, 3-е места первого ряда стадиона. Сколькими способами мальчики могут занять эти места? | Антон, Борис и Виктор купили 3 билета на футбол на 1-е, 2-е, 3-е места первого ряда стадиона. Сколькими способами мальчики могут занять эти места? | ||
| Строка 33: | Строка 36: | ||
Если один из мальчиков будет сидеть на первом месте то на втором месте может сидеть один из двух оставшихся, тогда третье место займет тот мальчик который остался. Итого 3*2*1=6 способов. | Если один из мальчиков будет сидеть на первом месте то на втором месте может сидеть один из двух оставшихся, тогда третье место займет тот мальчик который остался. Итого 3*2*1=6 способов. | ||
| − | [[Изображение:Задача на билеты.jpg]] | + | [[Изображение:Задача на билеты.jpg|500px]] |
| + | |||
| + | '''Задача 5.''' | ||
| + | Кросс осенний вспоминая, Спорят белки два часа: | ||
| + | |||
| + | - Победил в забеге заяц, | ||
| + | |||
| + | А второй была лиса! | ||
| + | |||
| + | Нет, твердит другая белка, - | ||
| + | |||
| + | Ты мне эти шутки брось. | ||
| + | |||
| + | Заяц был вторым, конечно, | ||
| + | |||
| + | Первым был, я помню, - лось | ||
| + | |||
| + | - Я, - промолвил филин важный, | ||
| + | |||
| + | В спор чужой не стану лезть, | ||
| + | |||
| + | Но у вас в словах у каждой | ||
| + | |||
| + | По одной ошибке есть | ||
| + | |||
| + | Белки фыркнули сердито, | ||
| + | |||
| + | Неприятно стало им, | ||
| + | |||
| + | Вы же, взвесив все, найдите, | ||
| + | |||
| + | Кто был первым, кто вторым | ||
| + | |||
| + | ''Решение'' | ||
| + | |||
| + | И в первом и во втором случае выходит, что заяц это – ложь. Следовательно, верный остается следующий вариант: | ||
| + | |||
| + | 1 – лось, 2 – лиса, 3 – заяц | ||
| + | |||
| + | |||
| + | '''Задача 6.''' | ||
| + | |||
| + | ни Воронов, ни Журавлев не умеют играть на баяне; | ||
| + | *Журавлев не знаком с Вороновым; | ||
| + | *писатель и художник в воскресенье уезжают на дачу к Павлову; | ||
| + | *писатель собирается написать очерк о Синицыне и Воронове. | ||
| + | *Требуется определить, кто есть кто. | ||
| + | |||
| + | ''Решение'' | ||
| + | |||
| + | Использовав табличный способ решения и наши логические рассуждения получаем | ||
| + | |||
| + | *Воронов – математик, | ||
| + | *Павлов – баянист, | ||
| + | *Журавлев – писатель | ||
| + | *Синицын – Художник. | ||
| + | |||
| + | '''Задача 7.''' | ||
| + | [[Изображение:Post-9-1212207616.jpg||thumb|200px|right]] | ||
| + | |||
| + | Однажды Винни-Пух захотел полакомиться медом и пошел к пчелам в гости. По дороге нарвал букет цветов, чтобы подарить труженицам пчелкам. Пчелки очень обрадовались, увидев мишку с букетом цветов, и сказали: «У нас есть большая бочка с медом. Мы дадим тебе меда, если ты сможешь с помощью двух сосудов вместимостью 3 л и 5 л налить себе 4 л!» Винни-Пух долго думал, но все-таки смог решить задачку. Как он это сделал? | ||
| + | |||
| + | ''Решение'' | ||
| + | |||
| + | способ I | ||
| + | |||
| + | [[Изображение:Задача_с_винипухом.jpg]] | ||
| + | |||
| + | способ II | ||
| + | |||
| + | [[Изображение:Задача с винипухом2.jpg]] | ||
| + | |||
| + | '''Задача 8.''' | ||
| + | |||
| + | Тому Сойеру нужно покрасить забор. Он имеет 12 л краски и хочет отлить из этого количества половину, но у него нет сосуда вместимостью в 6 л. У него 2 сосуда: один – вместимостью в 8 л, а другой – вместимостью в 5 л. Каким образом налить 6 л краски в сосуд на 8 л? Какое наименьшее число переливаний необходимо при этом сделать? | ||
| + | |||
| + | ''Решение'' | ||
| + | |||
| + | Сначала нужно налить 8 литров в 8л., потом из 8л. наливаете полный 5л., в результате получается, что в 12л. - 4 литра, в 8л - 3литра, а в 5л. - 5 литров. | ||
| + | Переливаете из 5л. в 12л. всю воду (или что там за жидкость), а из 8л. переливаете все 3 литра в 5л. В результате 9 литров в 12л, 0 литров в 8л., и 3 литра в 5л. | ||
| + | Переливаете из 12л. 8 литров в пустой 8л.,и в 12 л. остается 1 литр. | ||
| + | Из 8л. доливаете в 5л., пока 5л. не станет полным, (в 5л. было 3л., след. долили мы еще 2литра из 8л.) Тогда в 8л. как раз остается 6л. | ||
| + | |||
| + | [[Изображение:12345677777.jpg]] | ||
| + | |||
| + | '''Задача 9.''' | ||
| + | |||
| + | У Буратино есть 27 золотых монет. Но известно, что Кот Базилио заменил одну монету на фальшивую, а она по весу тяжелее настоящих. Как за три взвешивания на чашечных весах без гирь Буратино определить фальшивую монету? | ||
| + | |||
| + | ''Решение'' | ||
| + | |||
| + | '''1. Взвешивание'''. Разделим 27 монет на три кучки по 9 монет в каждой. Возьмем две кучки и положим их на весы. Если чашка с весами опуститься в низ, то в этой кучи фальшивая монета. Если чаши весов покажут равновесие, тогда фальшивая монета находится в кучке которая осталась в сторонке. Так мы нашли кучку в которой есть фальшивая монета. | ||
| + | |||
| + | '''2. Взвешивание.''' У нас осталось 9 монет, разделим их на три кучки по 3 монеты в каждой. На веси ложем две кучки по три монеты в каждой. Если чашка весов опустилась в низ, то в этой кучке фальшивая монета. Если вес моет одинаковый, то значит, фальшивая монета осталась в третей кучке в сторонке. | ||
| + | |||
| + | '''3. Взвешивание. '''У нас осталось 3 монеты, разделим их на три. Две монеты положим на чашу весов. Если чаша опустилась, то фальшивая монета находится на этой чаше. Если вес монет одинаковый то фальшивая монета, та которую не взвешивали. | ||
| + | |||
| + | |||
| + | '''Задача 10.''' | ||
| + | |||
| + | Дядюшке Скруджу принесли 8 одинаковых по виду монет, одна из которых не золотая, а фальшивая и легче других. Помогите Скруджу определить фальшивую монету. Какое минимальное число взвешиваний ему потребуется? | ||
| + | |||
| + | ''Решение'' | ||
| + | |||
| + | Разделим монеты на кучки по 3, 3, 2 монеты. Положим на чаши весов кучки по 3 монеты – по результату этого взвешивания мы точно узнаем, в какой из кучек находится фальшивка. | ||
| + | Если весы покажут равенство, то фальшивая монета в третьей кучке. Тогда кладем на чаши весов монеты из третьей кучки. Фальшивкой будет та, которая легче. Если весы покажут неравенство. Тогда кладем на чаши весов по монете из более легкой кучки; если установилось равенство, то фальшивкой является третья монета из этой кучки; если неравенство – то более легкая монета и есть фальшивка. Следовательно, потребуется два взвешивания | ||
| + | |||
| + | |||
| + | '''Задача 11.''' | ||
| + | |||
| + | Среди школьников шестого класса проводилось анкетирование по любимым мультфильмам. Самыми популярными оказались три мультфильма: «Белоснежка и семь гномов», «Губка Боб Квадратные Штаны», «Волк и теленок». Всего в классе 38 человек. «Белоснежку и семь гномов» выбрали 21 ученик, среди которых трое назвали еще «Волк и теленок», шестеро – «Губка Боб Квадратные Штаны», а один написал все три мультфильма. Мультфильм «Волк и теленок» назвали 13 ребят, среди которых пятеро выбрали сразу два мультфильма. Сколько человек выбрали мультфильм «Губка Боб Квадратные Штаны»? | ||
| + | |||
| + | |||
| + | ''Решение'' | ||
| + | |||
| + | [[Изображение:Диаграмма про кино.jpg]] | ||
| + | |||
| + | В этой задаче 3 множества, которые пересекаются между собой. | ||
| + | 23-3-6-1=11 – ребята выбрали только «Белоснежку и семь гномов» | ||
| + | 13-3-1-2=7 ребята смотрят «Волк и теленок» | ||
| + | 38-(11+3+1+6+2+7)=8 – человек смотрят «Губку Боб» | ||
| + | Делаем выводы, что «Губка Боб Квадратные штаны выбрали 8+2+1+6=17 человек. | ||
| + | |||
| + | '''Задача 12.''' | ||
| + | |||
| + | У Светланы 3 юбки и 5 кофт, удачно сочетающихся по цвету. Сколько различных комбинаций одежды имеется у Светланы? | ||
| + | |||
| + | ''Решение'' | ||
| + | |||
| + | 5*3=15 комбинаций одежд | ||
| + | |||
| + | '''Задача 13.''' | ||
| + | |||
| + | Сколькими способами можно выложить в ряд красный, черный, синий и зеленый шарики? | ||
| + | |||
| + | ''Решение'' | ||
| + | |||
| + | На первое место можно положить любой из четырех шариков, на второе – любой из трех оставшихся, на третье – любой из двух оставшихся, а на четвертое – последний оставшийся шарик. Итак, ответ: 4 * 3 *2 * 1 = 4 | ||
| + | |||
| + | '''Задача 14.''' | ||
| + | |||
| + | Сколькими способами можно поселить 7 студентов в три комнаты: одноместную, двухместную и четырехместную? | ||
| + | |||
| + | ''Решение'' | ||
| + | |||
| + | 7!/1!*2!*4!=5040/1*1*2*1*2*3*4=5040/48=105 способов размещения | ||
| + | |||
| + | '''Задача 15.''' | ||
| + | |||
| + | У двух начинающих коллекционеров по 20 марок и по 10 значков. Честным обменом называется обмен одной марки на одну марку или одного значка на один значок. Сколькими способами коллекционеры могут осуществить честный обмен? | ||
| + | |||
| + | ''Решение'' | ||
| + | |||
| + | 14!/(14-5)!=14!/9!=10*11*12*13*14=240240 способов | ||
| + | |||
| + | '''Задача 16.''' | ||
| + | |||
| + | . Сколькими способами можно составить расписание на день из 5 различных уроков, если изучается 14 предметов? | ||
| + | |||
| + | ''Решение'' | ||
| + | |||
| + | 14!/(14-5)!=14!/9!=10*11*12*13*14=240240 способов | ||
| + | |||
| + | '''Задача 17.''' | ||
| + | |||
| + | В кондитерском магазине продавались 4 сорта пирожных: эклеры, песочные, наполеоны и слоеные. Сколькими способами можно купить 7 пирожных. | ||
| + | |||
| + | ''Решение'' | ||
| + | |||
| + | 7!/(7-4)!=7!/3!=4*5*6*7=840 способов | ||
| + | |||
| + | '''Задача 18.''' | ||
| + | |||
| + | Три стрелка независимо друг от друга стреляют по цели. Вероятность попадания в цель для первого стрелка равна 0,75, для второго - 0,8, для третьего - 0,9. Определить вероятность того, что в цель попадёт хотя бы один стрелок. | ||
| + | |||
| + | ''Решение'' | ||
| + | |||
| + | Найдем вероятность противоположного события: | ||
| + | |||
| + | I стрелок 1-0,75=0,25 | ||
| + | |||
| + | II стрелок 1-0,8 = 0,2 | ||
| + | |||
| + | III стрелок 1-0,9 = 0,1 | ||
| + | |||
| + | Произведение всех трех событий: | ||
| + | |||
| + | 0,25*0,2*0,1=0,005 | ||
| + | |||
| + | Вероятность одного попадания равна 1-0,005=0,995 | ||
| + | |||
| + | '''Задача 19.''' | ||
| + | |||
| + | Подбрасываем две монетки. Какова вероятность выпадения хотя бы одного герба? | ||
| + | |||
| + | ''Решение'' | ||
| + | |||
| + | всего возможно 4 события: | ||
| + | |||
| + | - оба раза выпадают гербы; | ||
| + | |||
| + | - оба раза выпадают цифры; | ||
| + | |||
| + | - первый раз – герб, а второй – цифра; | ||
| + | |||
| + | |||
| + | - первый раз – цифра, а второй – герб. | ||
| + | |||
| + | Все 4 события равновозможные. | ||
| + | |||
| + | Вероятность выпадения двух орлов – 1/4, двух решек -1/4, одного орла и одной решки равна | ||
| + | |||
| + | 2/4=1/2 или 0,5 | ||
| + | |||
| + | '''Задача 20.''' | ||
| + | |||
| + | [[Медиа:Анкета_по_выявлению_учебных_интересов.doc|Анкета по выявлению учебных интересов]] | ||
| + | |||
| + | [[Категория:Проект ДООМ 2010-2011]] | ||
Текущая версия на 16:04, 11 января 2011
Задача 1.
Аня, Женя, Нина спросили, какие оценки им поставили за контрольную работу. Учитель ответил: «Плохих оценок нет. У вас троих оценки разные. У Ани не «3». У Нины не «3» и не «5». Кто какую оценку получил?
Решение У Нины может быть только "4". Остались две отметки " "3" и "5". А у Ани не "3", значит "5". Осталась одна отметка "3" у Жени.
Ответ:
Аня-5,Нина-4, Женя-3
Задача 2.
Три подруги были на выпускном балу в белом, красном и голубом платье. Их туфли были тех же трёх цветов. Только у Тамары цвета платья и туфель совпадали. Валя была в белых туфлях. Ни платье, ни туфли Лиды не были красными. Определите цвета платьев и туфель у подруг.
Решение Так как Валя была в белых туфлях, а у Нины ни туфли ни платья не были красными, остается Тамара у которой туфли красные. А мы знаем, что у Тамары туфли и платье одного цвета – красные. Значит у Вали голубое платье и белые туфли (так как у двух других платья и туфли ни совпали). Остается у Лиды беле платье и голубые туфли
Тамара красное платье и туфли, Лида белое платье и голубые туфли, Валя голубое платье и белые туфли,
Задача 3.
В Стране Чудес есть четыре города: А, Б и В и Г. Из города А в город Б ведет 6 дорог, а из города Б в город В – 4 дороги, Из города А в город Г – две дороги, и из города Г в город В – тоже две дороги. Сколькими способами можно проехать от А до В?
Решение
Из города А в город В можно добраться 6 дорогами, из города Б в город В 4 получаем 6*4=24 способами. Кроме того в город В можно добраться из А через город Г 2*2=4 способа. Складываем 24+4 = 28 дорог.
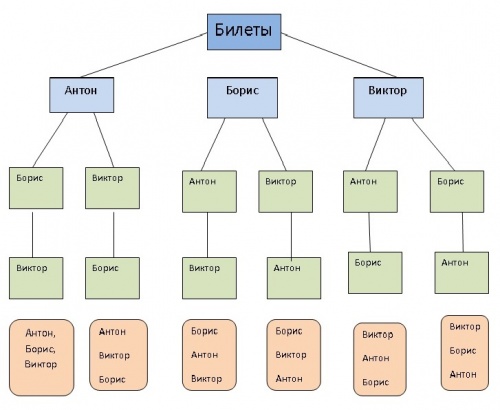
Задача 4.
Антон, Борис и Виктор купили 3 билета на футбол на 1-е, 2-е, 3-е места первого ряда стадиона. Сколькими способами мальчики могут занять эти места?
Решение Если один из мальчиков будет сидеть на первом месте то на втором месте может сидеть один из двух оставшихся, тогда третье место займет тот мальчик который остался. Итого 3*2*1=6 способов.
Задача 5. Кросс осенний вспоминая, Спорят белки два часа:
- Победил в забеге заяц,
А второй была лиса!
Нет, твердит другая белка, -
Ты мне эти шутки брось.
Заяц был вторым, конечно,
Первым был, я помню, - лось
- Я, - промолвил филин важный,
В спор чужой не стану лезть,
Но у вас в словах у каждой
По одной ошибке есть
Белки фыркнули сердито,
Неприятно стало им,
Вы же, взвесив все, найдите,
Кто был первым, кто вторым
Решение
И в первом и во втором случае выходит, что заяц это – ложь. Следовательно, верный остается следующий вариант:
1 – лось, 2 – лиса, 3 – заяц
Задача 6.
ни Воронов, ни Журавлев не умеют играть на баяне;
- Журавлев не знаком с Вороновым;
- писатель и художник в воскресенье уезжают на дачу к Павлову;
- писатель собирается написать очерк о Синицыне и Воронове.
- Требуется определить, кто есть кто.
Решение
Использовав табличный способ решения и наши логические рассуждения получаем
- Воронов – математик,
- Павлов – баянист,
- Журавлев – писатель
- Синицын – Художник.
Задача 7.
Однажды Винни-Пух захотел полакомиться медом и пошел к пчелам в гости. По дороге нарвал букет цветов, чтобы подарить труженицам пчелкам. Пчелки очень обрадовались, увидев мишку с букетом цветов, и сказали: «У нас есть большая бочка с медом. Мы дадим тебе меда, если ты сможешь с помощью двух сосудов вместимостью 3 л и 5 л налить себе 4 л!» Винни-Пух долго думал, но все-таки смог решить задачку. Как он это сделал?
Решение
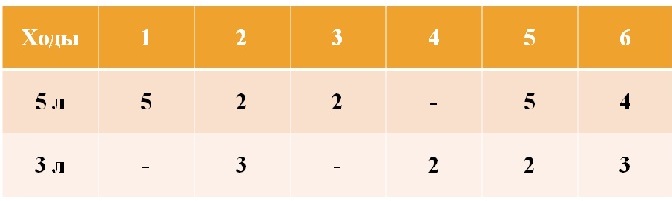
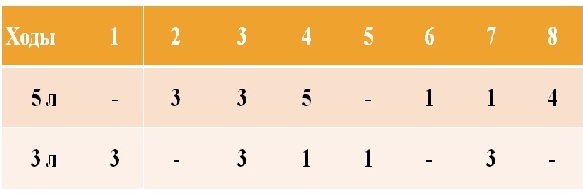
способ I
способ II
Задача 8.
Тому Сойеру нужно покрасить забор. Он имеет 12 л краски и хочет отлить из этого количества половину, но у него нет сосуда вместимостью в 6 л. У него 2 сосуда: один – вместимостью в 8 л, а другой – вместимостью в 5 л. Каким образом налить 6 л краски в сосуд на 8 л? Какое наименьшее число переливаний необходимо при этом сделать?
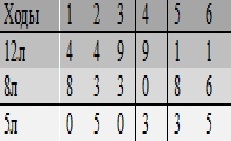
Решение
Сначала нужно налить 8 литров в 8л., потом из 8л. наливаете полный 5л., в результате получается, что в 12л. - 4 литра, в 8л - 3литра, а в 5л. - 5 литров. Переливаете из 5л. в 12л. всю воду (или что там за жидкость), а из 8л. переливаете все 3 литра в 5л. В результате 9 литров в 12л, 0 литров в 8л., и 3 литра в 5л. Переливаете из 12л. 8 литров в пустой 8л.,и в 12 л. остается 1 литр. Из 8л. доливаете в 5л., пока 5л. не станет полным, (в 5л. было 3л., след. долили мы еще 2литра из 8л.) Тогда в 8л. как раз остается 6л.
Задача 9.
У Буратино есть 27 золотых монет. Но известно, что Кот Базилио заменил одну монету на фальшивую, а она по весу тяжелее настоящих. Как за три взвешивания на чашечных весах без гирь Буратино определить фальшивую монету?
Решение
1. Взвешивание. Разделим 27 монет на три кучки по 9 монет в каждой. Возьмем две кучки и положим их на весы. Если чашка с весами опуститься в низ, то в этой кучи фальшивая монета. Если чаши весов покажут равновесие, тогда фальшивая монета находится в кучке которая осталась в сторонке. Так мы нашли кучку в которой есть фальшивая монета.
2. Взвешивание. У нас осталось 9 монет, разделим их на три кучки по 3 монеты в каждой. На веси ложем две кучки по три монеты в каждой. Если чашка весов опустилась в низ, то в этой кучке фальшивая монета. Если вес моет одинаковый, то значит, фальшивая монета осталась в третей кучке в сторонке.
3. Взвешивание. У нас осталось 3 монеты, разделим их на три. Две монеты положим на чашу весов. Если чаша опустилась, то фальшивая монета находится на этой чаше. Если вес монет одинаковый то фальшивая монета, та которую не взвешивали.
Задача 10.
Дядюшке Скруджу принесли 8 одинаковых по виду монет, одна из которых не золотая, а фальшивая и легче других. Помогите Скруджу определить фальшивую монету. Какое минимальное число взвешиваний ему потребуется?
Решение
Разделим монеты на кучки по 3, 3, 2 монеты. Положим на чаши весов кучки по 3 монеты – по результату этого взвешивания мы точно узнаем, в какой из кучек находится фальшивка. Если весы покажут равенство, то фальшивая монета в третьей кучке. Тогда кладем на чаши весов монеты из третьей кучки. Фальшивкой будет та, которая легче. Если весы покажут неравенство. Тогда кладем на чаши весов по монете из более легкой кучки; если установилось равенство, то фальшивкой является третья монета из этой кучки; если неравенство – то более легкая монета и есть фальшивка. Следовательно, потребуется два взвешивания
Задача 11.
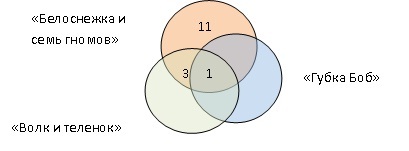
Среди школьников шестого класса проводилось анкетирование по любимым мультфильмам. Самыми популярными оказались три мультфильма: «Белоснежка и семь гномов», «Губка Боб Квадратные Штаны», «Волк и теленок». Всего в классе 38 человек. «Белоснежку и семь гномов» выбрали 21 ученик, среди которых трое назвали еще «Волк и теленок», шестеро – «Губка Боб Квадратные Штаны», а один написал все три мультфильма. Мультфильм «Волк и теленок» назвали 13 ребят, среди которых пятеро выбрали сразу два мультфильма. Сколько человек выбрали мультфильм «Губка Боб Квадратные Штаны»?
Решение
В этой задаче 3 множества, которые пересекаются между собой. 23-3-6-1=11 – ребята выбрали только «Белоснежку и семь гномов» 13-3-1-2=7 ребята смотрят «Волк и теленок» 38-(11+3+1+6+2+7)=8 – человек смотрят «Губку Боб» Делаем выводы, что «Губка Боб Квадратные штаны выбрали 8+2+1+6=17 человек.
Задача 12.
У Светланы 3 юбки и 5 кофт, удачно сочетающихся по цвету. Сколько различных комбинаций одежды имеется у Светланы?
Решение
5*3=15 комбинаций одежд
Задача 13.
Сколькими способами можно выложить в ряд красный, черный, синий и зеленый шарики?
Решение
На первое место можно положить любой из четырех шариков, на второе – любой из трех оставшихся, на третье – любой из двух оставшихся, а на четвертое – последний оставшийся шарик. Итак, ответ: 4 * 3 *2 * 1 = 4
Задача 14.
Сколькими способами можно поселить 7 студентов в три комнаты: одноместную, двухместную и четырехместную?
Решение
7!/1!*2!*4!=5040/1*1*2*1*2*3*4=5040/48=105 способов размещения
Задача 15.
У двух начинающих коллекционеров по 20 марок и по 10 значков. Честным обменом называется обмен одной марки на одну марку или одного значка на один значок. Сколькими способами коллекционеры могут осуществить честный обмен?
Решение
14!/(14-5)!=14!/9!=10*11*12*13*14=240240 способов
Задача 16.
. Сколькими способами можно составить расписание на день из 5 различных уроков, если изучается 14 предметов?
Решение
14!/(14-5)!=14!/9!=10*11*12*13*14=240240 способов
Задача 17.
В кондитерском магазине продавались 4 сорта пирожных: эклеры, песочные, наполеоны и слоеные. Сколькими способами можно купить 7 пирожных.
Решение
7!/(7-4)!=7!/3!=4*5*6*7=840 способов
Задача 18.
Три стрелка независимо друг от друга стреляют по цели. Вероятность попадания в цель для первого стрелка равна 0,75, для второго - 0,8, для третьего - 0,9. Определить вероятность того, что в цель попадёт хотя бы один стрелок.
Решение
Найдем вероятность противоположного события:
I стрелок 1-0,75=0,25
II стрелок 1-0,8 = 0,2
III стрелок 1-0,9 = 0,1
Произведение всех трех событий:
0,25*0,2*0,1=0,005
Вероятность одного попадания равна 1-0,005=0,995
Задача 19.
Подбрасываем две монетки. Какова вероятность выпадения хотя бы одного герба?
Решение
всего возможно 4 события:
- оба раза выпадают гербы;
- оба раза выпадают цифры;
- первый раз – герб, а второй – цифра;
- первый раз – цифра, а второй – герб.
Все 4 события равновозможные.
Вероятность выпадения двух орлов – 1/4, двух решек -1/4, одного орла и одной решки равна
2/4=1/2 или 0,5
Задача 20.
Анкета по выявлению учебных интересов