Десятичная система счисления
TopT (обсуждение | вклад) |
TopT (обсуждение | вклад) |
||
| (не показаны 6 промежуточных версий 2 участников) | |||
| Строка 1: | Строка 1: | ||
| + | Автор-составитель: Миронов | ||
| + | |||
ДЕСЯТИЧНАЯ СИСТЕМА СЧИСЛЕНИЯ, способ записи чисел, при котором один и тот же знак (цифра) из десяти: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 имеет различные значения в зависимости от того места, где он расположен. Десять единиц 1-го разряда (места, занимаемого в числе) образуют единицу следующего разряда - число 10, десять единиц 2-го разряда образуют единицу 3-го разряда - число 100 и т.д. Например, 362=3Ч100+6Ч10+2. Для обозначения больших чисел употребляется (с 14 в.) слово "миллион" (1000000) и его степени (с 15 в.): биллион (миллиард) 106?2 триллион 106?3 квадриллион 106?4 квинтиллион 106?5 секстиллион 106?6 септиллион 106?7 окталлион 106?8 нонниллион 106?9 С 17 в. во Франции и некоторых других странах биллионом стали называть число 109, триллионом 1012, квадриллионом 1015 и т.д. Однако в Великобритании, Германии и некоторых других странах прежнее значение слов сохранилось. | ДЕСЯТИЧНАЯ СИСТЕМА СЧИСЛЕНИЯ, способ записи чисел, при котором один и тот же знак (цифра) из десяти: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 имеет различные значения в зависимости от того места, где он расположен. Десять единиц 1-го разряда (места, занимаемого в числе) образуют единицу следующего разряда - число 10, десять единиц 2-го разряда образуют единицу 3-го разряда - число 100 и т.д. Например, 362=3Ч100+6Ч10+2. Для обозначения больших чисел употребляется (с 14 в.) слово "миллион" (1000000) и его степени (с 15 в.): биллион (миллиард) 106?2 триллион 106?3 квадриллион 106?4 квинтиллион 106?5 секстиллион 106?6 септиллион 106?7 окталлион 106?8 нонниллион 106?9 С 17 в. во Франции и некоторых других странах биллионом стали называть число 109, триллионом 1012, квадриллионом 1015 и т.д. Однако в Великобритании, Германии и некоторых других странах прежнее значение слов сохранилось. | ||
Целое число x в десятичной системе счисления представляется в виде конечной линейной комбинации степеней числа 10: | Целое число x в десятичной системе счисления представляется в виде конечной линейной комбинации степеней числа 10: | ||
| − | [[Изображение: | + | [[Изображение:Exa1mple.jpg]] ,где [[Изображение:Example1.jpg]] это целые числа, называемые цифрами, удовлетворяющие неравенству [[Изображение:Example2.jpg]] |
PS:где n — число разрядов целой части числа, m — число разрядов дробной части числа! | PS:где n — число разрядов целой части числа, m — число разрядов дробной части числа! | ||
[[Изображение:Example3.jpg]] | [[Изображение:Example3.jpg]] | ||
[[Изображение:Example4.jpg]] | [[Изображение:Example4.jpg]] | ||
| + | |||
Дополнительный материал по ссылкам ниже: | Дополнительный материал по ссылкам ниже: | ||
| + | |||
[http://bse.sci-lib.com/article024435.html тут] | [http://bse.sci-lib.com/article024435.html тут] | ||
| + | |||
[http://www.pandia.ru/271830/ и вот тут] | [http://www.pandia.ru/271830/ и вот тут] | ||
| + | |||
--[[Участник:TopT|TopT]] 07:35, 16 сентября 2011 (MSD) | --[[Участник:TopT|TopT]] 07:35, 16 сентября 2011 (MSD) | ||
| + | |||
| + | [[Категория: Информатика и ИКТ]] | ||
| + | [http://master-test.net/ru/teacher/quiz/editor/id/9710 Тест] | ||
Текущая версия на 10:46, 28 сентября 2011
Автор-составитель: Миронов
ДЕСЯТИЧНАЯ СИСТЕМА СЧИСЛЕНИЯ, способ записи чисел, при котором один и тот же знак (цифра) из десяти: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 имеет различные значения в зависимости от того места, где он расположен. Десять единиц 1-го разряда (места, занимаемого в числе) образуют единицу следующего разряда - число 10, десять единиц 2-го разряда образуют единицу 3-го разряда - число 100 и т.д. Например, 362=3Ч100+6Ч10+2. Для обозначения больших чисел употребляется (с 14 в.) слово "миллион" (1000000) и его степени (с 15 в.): биллион (миллиард) 106?2 триллион 106?3 квадриллион 106?4 квинтиллион 106?5 секстиллион 106?6 септиллион 106?7 окталлион 106?8 нонниллион 106?9 С 17 в. во Франции и некоторых других странах биллионом стали называть число 109, триллионом 1012, квадриллионом 1015 и т.д. Однако в Великобритании, Германии и некоторых других странах прежнее значение слов сохранилось.
Целое число x в десятичной системе счисления представляется в виде конечной линейной комбинации степеней числа 10:
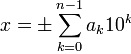,где 
это целые числа, называемые цифрами, удовлетворяющие неравенству 
PS:где n — число разрядов целой части числа, m — число разрядов дробной части числа!
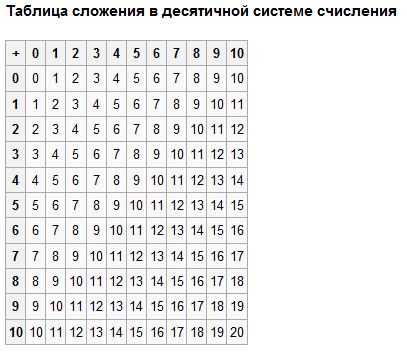
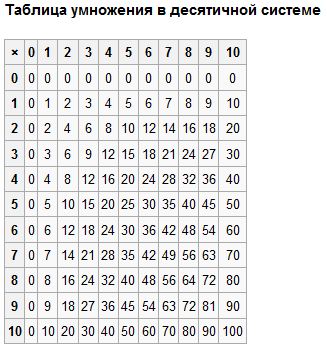
Дополнительный материал по ссылкам ниже:
