Фибоначчиева система счисления
Бетева (обсуждение | вклад) (Новая: '''Фибоначчиева система счисления''' — смешанная система счисления для целых чисел на основе чисел Фиб...) |
Бетева (обсуждение | вклад) |
||
| (не показаны 9 промежуточных версий 1 участника) | |||
| Строка 1: | Строка 1: | ||
| + | Автор-составитель : [http://www.tgl.net.ru/wiki/index.php/Участник:Бетева Бетева] | ||
| + | |||
| + | |||
'''Фибоначчиева система счисления''' — смешанная система счисления для целых чисел на основе чисел Фибоначчи F2=1, F3=2, F4=3, F5=5, F6=8 и т.д. | '''Фибоначчиева система счисления''' — смешанная система счисления для целых чисел на основе чисел Фибоначчи F2=1, F3=2, F4=3, F5=5, F6=8 и т.д. | ||
'''Последовательность Фибоначчи''' определяется следующим образом: | '''Последовательность Фибоначчи''' определяется следующим образом: | ||
| − | + | ||
| − | + | [[Изображение:Ф0.png]] | |
| − | + | [[Изображение:Ф1.png]] | |
| + | [[Изображение:Фн.png]] | ||
| + | |||
Несколько первых её членов : | Несколько первых её членов : | ||
| − | + | [[Изображение:Нескпер.png]] | |
''' История''' | ''' История''' | ||
| Строка 26: | Строка 31: | ||
* Из предыдущего равенства при k = n вытекает: | * Из предыдущего равенства при k = n вытекает: | ||
[[Изображение:Из_предыд_равенства.png]] | [[Изображение:Из_предыд_равенства.png]] | ||
| + | |||
| + | * НОД-равенство: | ||
| + | [[Изображение:Нод_равенство.png]] | ||
| + | |||
| + | '''Фибоначчиева система счисления''' | ||
| + | |||
| + | Теорема Цекендорфа утверждает, что любое натуральное число n можно представить единственным образом в виде суммы чисел Фибоначчи: | ||
| + | |||
| + | [[Изображение:Суммчислфиб.png]] | ||
| + | |||
| + | где k1 >= k2+2, k2 >= k3+2, ... , kr >= 2 (т.е. в записи нельзя использовать два соседних числа Фибоначчи). | ||
| + | |||
| + | Отсюда следует, что любое число можно однозначно записать в фибоначчиевой системе счисления, например: | ||
| + | |||
| + | [[Изображение:Отсюдаслед.png]] | ||
| + | [[Изображение:Отсюдаслед2.png]] | ||
| + | [[Изображение:Отсюдаслед3.png]] | ||
| + | |||
| + | причём ни в каком числе не могут идти две единицы подряд. | ||
| + | |||
| + | Нетрудно получить и правило прибавления единицы к числу в фибоначчиевой системе счисления: если младшая цифра равна 0, то её заменяем на 1, а если равна 1 (т.е. в конце стоит 01), то 01 заменяем на 10. Затем "исправляем" запись, последовательно исправляя везде 011 на 100. В результате за линейное время будет получена запись нового числа. | ||
| + | |||
| + | Перевод числа в фибоначчиеву систему счисления осуществляется простым "жадным" алгоритмом: просто перебираем числа Фибоначчи от больших к меньшим и, если некоторое [[Изображение:Некоторое.png]] , то [[Изображение:Фк.png]] входит в запись числа [[Изображение:Ннн.png]], и мы отнимаем [[Изображение:Фк.png]] от [[Изображение:Ннн.png]] и продолжаем поиск. | ||
| + | |||
| + | '''В теории информации''' | ||
| + | |||
| + | На основе фибоначчиевой системы счисления строится код (кодирование) Фибоначчи — универсальный код для натуральных чисел (1, 2, 3…), использующий последовательности битов. Поскольку комбинация 11 запрещена в Фибоначчиевой системе счисления, её можно использовать как маркер конца записи. Для составления кода Фибоначчи по записи числа в фибоначчиевой системе счисления следует переписать цифры в обратном порядке (так, что старшая единица оказывается последним символом) и приписать в конце ещё раз 1 (см. таблицу). То есть, кодовая последовательность имеет вид: | ||
| + | |||
| + | ε2ε3…εn1, | ||
| + | |||
| + | где n — номер самого старшего разряда с единицей. | ||
| + | |||
| + | '''Арифметика''' | ||
| + | |||
| + | Сложение чисел в позиционных системах счисления выполняется с использованием переноса, позволяющего устранять последствия переполнения разряда. Например, в двоичной системе: 01 + 01 = 02 = 10. | ||
| + | |||
| + | В фибоначчиевой системе счисления дело обстоит сложнее: | ||
| + | |||
| + | * Во-первых, вес старших разрядов не является кратным весу разряда, из которого требуется перенос. При сложении двух единиц в одном разряде требуется перенос не только влево, но и вправо: 0200 = 1001. При переносе в отсутствующие разряды ε1 и ε0 следует помнить, что | ||
| + | F1=1=F2 и F0=0. | ||
| + | * Во-вторых, требуется избавляться от соседних единиц: 011 = 100. Правило для раскрытия двоек является следствием этого равенства: | ||
| + | 0200 = 0100 + 0011 = 0111 = 1001. | ||
| + | |||
| + | '''Источники:''' | ||
| + | [http://www.e-maxx.ru/algo/fibonacci_numbers] | ||
| + | [http://ru.wikipedia.org/wiki/%D0%A4%D0%B8%D0%B1%D0%BE%D0%BD%D0%B0%D1%87%D1%87%D0%B8%D0%B5%D0%B2%D0%B0_%D1%81%D0%B8%D1%81%D1%82%D0%B5%D0%BC%D0%B0_%D1%81%D1%87%D0%B8%D1%81%D0%BB%D0%B5%D0%BD%D0%B8%D1%8F] | ||
| + | |||
| + | |||
| + | [[Категория: Информатика и ИКТ]] | ||
Текущая версия на 11:20, 20 сентября 2011
Автор-составитель : Бетева
Фибоначчиева система счисления — смешанная система счисления для целых чисел на основе чисел Фибоначчи F2=1, F3=2, F4=3, F5=5, F6=8 и т.д.
Последовательность Фибоначчи определяется следующим образом:
История
Эти числа ввёл в 1202 г. Леонардо Фибоначчи (Leonardo Fibonacci) (также известный как Леонардо Пизанский (Leonardo Pisano)). Однако именно благодаря математику 19 века Люка (Lucas) название "числа Фибоначчи" стало общеупотребительным. Впрочем, индийские математики упоминали числа этой последовательности ещё раньше: Гопала (Gopala) до 1135 г., Хемачандра (Hemachandra) — в 1150 г.
Свойства
Числа Фибоначчи обладают множеством интересных математических свойств.
Вот лишь некоторые из них:
* Соотношение Кассини:
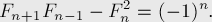
* Правило "сложения":
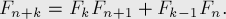
* Из предыдущего равенства при k = n вытекает:
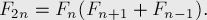
* НОД-равенство:
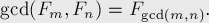
Фибоначчиева система счисления
Теорема Цекендорфа утверждает, что любое натуральное число n можно представить единственным образом в виде суммы чисел Фибоначчи:
где k1 >= k2+2, k2 >= k3+2, ... , kr >= 2 (т.е. в записи нельзя использовать два соседних числа Фибоначчи).
Отсюда следует, что любое число можно однозначно записать в фибоначчиевой системе счисления, например:
причём ни в каком числе не могут идти две единицы подряд.
Нетрудно получить и правило прибавления единицы к числу в фибоначчиевой системе счисления: если младшая цифра равна 0, то её заменяем на 1, а если равна 1 (т.е. в конце стоит 01), то 01 заменяем на 10. Затем "исправляем" запись, последовательно исправляя везде 011 на 100. В результате за линейное время будет получена запись нового числа.
Перевод числа в фибоначчиеву систему счисления осуществляется простым "жадным" алгоритмом: просто перебираем числа Фибоначчи от больших к меньшим и, если некоторое ![]() , то
, то ![]() входит в запись числа
входит в запись числа ![]() , и мы отнимаем
, и мы отнимаем ![]() от
от ![]() и продолжаем поиск.
и продолжаем поиск.
В теории информации
На основе фибоначчиевой системы счисления строится код (кодирование) Фибоначчи — универсальный код для натуральных чисел (1, 2, 3…), использующий последовательности битов. Поскольку комбинация 11 запрещена в Фибоначчиевой системе счисления, её можно использовать как маркер конца записи. Для составления кода Фибоначчи по записи числа в фибоначчиевой системе счисления следует переписать цифры в обратном порядке (так, что старшая единица оказывается последним символом) и приписать в конце ещё раз 1 (см. таблицу). То есть, кодовая последовательность имеет вид:
ε2ε3…εn1,
где n — номер самого старшего разряда с единицей.
Арифметика
Сложение чисел в позиционных системах счисления выполняется с использованием переноса, позволяющего устранять последствия переполнения разряда. Например, в двоичной системе: 01 + 01 = 02 = 10.
В фибоначчиевой системе счисления дело обстоит сложнее:
* Во-первых, вес старших разрядов не является кратным весу разряда, из которого требуется перенос. При сложении двух единиц в одном разряде требуется перенос не только влево, но и вправо: 0200 = 1001. При переносе в отсутствующие разряды ε1 и ε0 следует помнить, что
F1=1=F2 и F0=0.
* Во-вторых, требуется избавляться от соседних единиц: 011 = 100. Правило для раскрытия двоек является следствием этого равенства:
0200 = 0100 + 0011 = 0111 = 1001.
