Семинар ДООМ Окружность и круг
Дамира (обсуждение | вклад) |
Дамира (обсуждение | вклад) |
||
| (не показаны 2 промежуточные версии 1 участника) | |||
| Строка 240: | Строка 240: | ||
2)Почему для вычерчивания окружности используют циркуль и почему колеса делают круглыми, а, например, не квадратными или треугольными? | 2)Почему для вычерчивания окружности используют циркуль и почему колеса делают круглыми, а, например, не квадратными или треугольными? | ||
| + | |||
| + | 3)"Классные инструменты в классе" | ||
| + | Знакомство со средствами визуализации сервиса Classtools, позволяющими организовать сетевое взаимодействие школьников | ||
| + | Дидактический материал[http://classtools.net/widgets/quiz_5/n6Wlb.htm '''''Найди продолжение'''''] | ||
| + | |||
[[Категория:Проект ДООМ 2009-2010]] | [[Категория:Проект ДООМ 2009-2010]] | ||
Текущая версия на 18:03, 19 ноября 2011
Участник: Молдагалиева Дамира Ароновна, IDm063
Предметная область: математика
Тема урока: Окружность и круг.(3ч). Первый урок.
Класс: 5
Учебник: И.И. Зубарева, А.Г. Мордкович.
Цели:
1) Создать условия контроля знаний и умений для изучения новой темы.
2) Содействовать воспитанию интереса к предмету, иллюстрируя параллельно процесс получения знаний в школе с жизненной ситуацией, знакомство с историей возникновения математических понятий, приобретение навыков исследовательской работы, воспитывать в детях чувство локтя и ответственность друг за друга.
3) Обеспечить в процессе преподавания сохранение здоровья учащихся.
Подготовка к уроку: компьютер, интерактивная доска, сундучок, напечатанные в WORD задания
Учитель: Сегодня нам предстоит изучение новой темы «Окружность и круг». Древние греки считали окружность и круг воплощением совершенства. В русском языке слово «круглый» стало обозначать высокую степень чего-либо. Мы говорим: «круглый отличник», «круглый сирота», «круглый год» и т.д. Обращение учителя к классу: привести пример из окружающей обстановки, имеющей форму круга.( Дети отвечают)
1. Учитель: Сегодня мы с вами побываем в цирке. Цирковая арена имеет форму круга. Причем, в какой бы стране мира мы не побывали бы, везде, где есть цирк, цирковая арена одинаковых размеров. А как вы думаете, ребята, почему? (Ответ: Артисты цирка часто выезжают на гастроли, и если бы арены не были стандартными, то приходилось бы терять много времени на привыкание к новой площадке, на корректировку программы, а ведь речь идет не только о людях, но и о животных. При работе с животными очень важно не нарушать условий дрессировки.).
Итак, мы в фойе здания. К нам подходит клоун, чтобы с нами познакомиться. В руке у него золотой сундучок. Он обещает приз тому, кто отгадает, что в сундучке. То, что лежит в этом волшебном сундучке, изобрел очень талантливый юноша, который придумал гончарный круг, первую в мире пилу. Под пеплом Помпеи археологи обнаружили много таких предметов, изготовленных из бронзы. В нашей стране это было обнаружено при раскопках в Нижнем Новгороде. В Древней Греции умение пользоваться этим предметом считалось верхом мастерства, а уж умение решать задачи с его помощью-признаком большого ума и высокого положения в обществе. Этот предмет незаменим в архитектуре и строительстве. За многие сотни лет конструкция его не изменилась. В настоящее время им умеет пользоваться любой школьник. Вопрос: что лежит в золотом сундучке?
Чтобы облегчить поиск ответа учитель предлагает задание на повторение: (фронтальная работа)
| 7/15 | 24 | 12 | 7/60 | 22/45 | 0 | 58/10 |
| ц | и | р | к | у | л | ь |
1.Найдите х. х/18=2/3; Р
2.Что больше:7/15или22/45? У
3.Назвать правильную дробь: 15/15; 26/15; 7/15; Ц
4.Перевести в неправильную дробь: 5,8. Ь
5.Какую часть часа составляет 7 минут? К
6.Задание по принципу игры «Устами младенца.» Л
• Бывают в счете футбольного матча - 5 баллов.
• Никогда не стоит первым - 4 балла.
• Особое правило при делении - 3 балла.
• Меньше единицы. - 2 балла.
• Не относят к натуральным числам - 1 балл.
7.Найти число, если 2/3 его равны 16. И
Дети записывают полученные баллы в индивидуальную карту ученика. Текст у каждого на столе в напечатанном виде и сопровождается показом на экране.
Значит, для построения окружности используют циркуль, а цирк и циркуль – слова-родственники, потому что оба происходят от латинского «циркус», т.е. круг.
Цирк, конечно, не может обойтись без факира. Он предлагает выполнить за ним следующие указания: представьте, что в середине острова стоит остроконечная башня, а от нее расходятся прямые улицы. Все они ведут к морю. Чтобы жители не упали в воду, вся территория обнесена красным канатом. Нарисуйте у себя в тетради этот остров с помощью циркуля. ( Дети с помощью учителя чертят окружность.)
Каждый раз, когда мы чертим окружность, остается точка от иголки циркуля. Эта точка называется центром окружности. Слово « центр» произошло от латинского слова «центриум» - палка с заостренным концом, которой погоняли быков; позднее оно стало означать заостренную ножку циркуля, а потом и точку, которую оставляет циркуль на листе бумаги. Улиц в городе много, но по какой идти, чтобы добраться от моря к башне? Проведите несколько дорог на чертеже вашего города. Измерьте их длины. Сделайте вывод. ( Все дороги имеют одинаковую длину). У этих дорог-отрезков есть название-радиус. Давайте общими усилиями скажем, что такое радиус.( Радиус-отрезок, соединяющий центр окружности с любой точкой окружности.) Колесо - одно из великих достижений человечества, которое было изобретено в 4 веке до н.э. на Древнем Востоке. «Радиус» переводится как «спица колеса».
Вопросы классу: • Для чего нужна была геометрия в этом изобретении?
• Где расположена ось колеса?
Факир:Пройдемся по нашему городу. Его жители очень любят играть в кегли.
Смысл игры заключается в том, чтобы шаром сбить кегли, стоящую по кругу. Выигрывает тот, кто сбивает кеглю, стоящую дальше других.
Начертите в тетрадях окружность. Нарисуйте шар и кегли, измерьте расстояния от шара до кеглей. Отметьте самое большое расстояние. Самое большое расстояние - это отрезок, проходящий через центр и соединяющий две точки окружности. Называется этот отрезок- диаметр. Диаметр ( в переводе с греческого) - отрезок, соединяющий две точки окружности и проходящий через центр.
Вопрос: Как связаны между собой радиус и диаметр?
Из скольких радиусов состоит диаметр?
Окружность мы нарисовали,
На ней две точки разных взяли,
Отрезком их соединим,
Ему название дадим.
Отрезок именуют гордо:
Ведь он не что-нибудь,
а …(хорда).
Окружность - удивительно гармоничная фигура; древние греки считали ее самой совершенной. Совершенство окружности - в расположении всех ее точек на одинаковом расстоянии от центра. Именно окружность - единственная кривая, которая может «скользить сама по себе», вращаясь вокруг центра.
Вопросы факиру. (если есть)
Учитель: В своей речи я употребила слова «окружность» и «круг». Это одно и тоже или нет?
У круга есть одна подруга,
Знакома всем ее наружность:
Она идет по краю круга
И называется окружность.
Окружность - линия, все точки которой расположены на одинаковом расстоянии от центра.
Круг- часть плоскости, ограниченная окружностью.
Основное свойство окружности дает ответ на вопросы, почему для ее вычерчивания используют циркуль и почему колеса делают круглыми, а, например, не квадратными или треугольными? Подумайте и вы над этими вопросами дома.
Поработаем с правилами геометрических понятий. На карточках написано начало правила, а на отдельных листочках - их продолжения. Найдите для каждого правила его продолжение. ( работа в парах).
| Окружность- замкнутая линия … | …все точки которой расположены на одинаковом расстоянии от центра. |
|---|---|
| Круг- часть плоскости… | …ограниченная окружностью. |
| Радиус-отрезок… | …соединяющий центр окружности с любой точкой окружности. |
| Диаметр - отрезок… | …соединяющий две точки окружности и проходящий через центр. |
| Хорда-это отрезок, соединяющий… | …две точки окружности. |
| Диаметр-это хорда.. | …проходящая через центр. |
Повторив правила новых геометрических понятий, поработаем самостоятельно. Для каждого из понятий подберите соответствующий ему рисунок.
| Круг | Радиус | Окружность | Хорда | Центр | Диаметр |
|---|
Оценка 5 - без единой ошибки
Оценка 4 - 1 ошибка
Оценка 3 - 2 ошибки
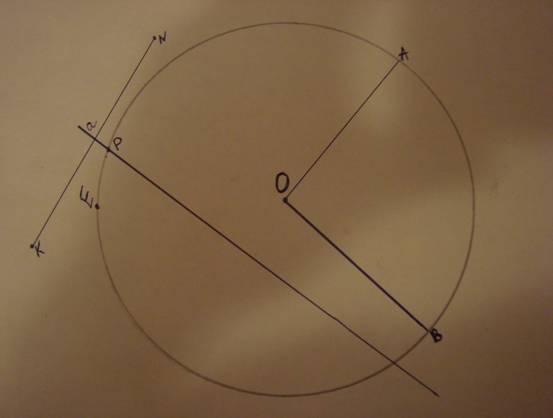
• Назовите точки, принадлежащие окружности.
• Назовите точки, принадлежащие кругу.
• Пересекает ли прямая или отрезок окружность.
• Назовите центр окружности.
• Отмечен ли радиус у данной окружности? Назовите его.
• Какие точки не принадлежит ни окружности, ни прямой?
• Показан ли диаметр данной окружности?
По итогам урока учащиеся сдают индивидуальные карты. При проверке можно увидеть, кто понял новую тему, а кто нет. На втором уроке данной темы провести корректирующую работу.
| № | Вид контроля | Вид задания | Оценка |
|---|---|---|---|
| 1. | Устные упражнения | ||
| 2. | Взаимоконтроль | Работа по карточкам(обучающий) | |
| 3. | контроль и взаимоконтроль | Задания по новой теме |
Рефлексия:
1. Что для себя нового узнали на уроке?
2. Что понравилось, а что нет?
- Выбор учащимися картинок по итогам урока.
Домашняя работа.
1)№412
2)Почему для вычерчивания окружности используют циркуль и почему колеса делают круглыми, а, например, не квадратными или треугольными?
3)"Классные инструменты в классе" Знакомство со средствами визуализации сервиса Classtools, позволяющими организовать сетевое взаимодействие школьников Дидактический материалНайди продолжение