Блиц-конкурс ДООМ
(→Команда 120 "ГРАФиТЫ") |
Nika (обсуждение | вклад) |
||
| (не показаны 2 промежуточные версии 2 участников) | |||
| Строка 664: | Строка 664: | ||
Из Ленинграда вылетел прямо на север дирижабль. Пролетев в северном направлении 500км, он повернул на восток. Пролетев в эту сторону 500км, дирижабль сделал новый поворот - на юг и прошел в южном направлении 500км. Затем он повернул на запад и, пролетев 500км, опустился на землю. Спрашивается: где расположено место спуска дирижабля относительно Ленинграда - к западу, к востоку, к северу или к югу?<br> | Из Ленинграда вылетел прямо на север дирижабль. Пролетев в северном направлении 500км, он повернул на восток. Пролетев в эту сторону 500км, дирижабль сделал новый поворот - на юг и прошел в южном направлении 500км. Затем он повернул на запад и, пролетев 500км, опустился на землю. Спрашивается: где расположено место спуска дирижабля относительно Ленинграда - к западу, к востоку, к северу или к югу?<br> | ||
id_122 - 0б<br> | id_122 - 0б<br> | ||
| + | id_102 - 0б<br> | ||
Решение.<br> | Решение.<br> | ||
На первый взгляд можно подумать, что задача содержит противоречие. Но дирижабль летел не по контуру квадрата, а по шарообразной форме Земли. Медианы к северу сближаются, поэтому, пройдя 500км по параллельному кругу, расположенному на 500 км севернее широты Ленинграда, дирижабль отошел к востоку на большее число градусов, чем пролетел потом в обратном направлении. В результате дирижабль, закончив полет, оказался восточнее Ленинграда.<br> | На первый взгляд можно подумать, что задача содержит противоречие. Но дирижабль летел не по контуру квадрата, а по шарообразной форме Земли. Медианы к северу сближаются, поэтому, пройдя 500км по параллельному кругу, расположенному на 500 км севернее широты Ленинграда, дирижабль отошел к востоку на большее число градусов, чем пролетел потом в обратном направлении. В результате дирижабль, закончив полет, оказался восточнее Ленинграда.<br> | ||
| Строка 707: | Строка 708: | ||
id_122 - 5б<br> | id_122 - 5б<br> | ||
id_120 - 5б<br> | id_120 - 5б<br> | ||
| + | id_102 - 5б<br> | ||
| + | |||
Решение.<br> | Решение.<br> | ||
Можно начертить данную фигуру, т.к. если пересечения линий обозначить вершинами, то все они четные, значит, по закономерности можно начертить данную фигуру одним росчерком пера.<br> | Можно начертить данную фигуру, т.к. если пересечения линий обозначить вершинами, то все они четные, значит, по закономерности можно начертить данную фигуру одним росчерком пера.<br> | ||
| Строка 716: | Строка 719: | ||
id_114 - 5б<br> | id_114 - 5б<br> | ||
id_120 - 5б<br> | id_120 - 5б<br> | ||
| + | id_102 - 1б<br> | ||
<br> | <br> | ||
Решение.<br> | Решение.<br> | ||
| Строка 735: | Строка 739: | ||
id_114 - 5б<br> | id_114 - 5б<br> | ||
id_103 - 5б <br> | id_103 - 5б <br> | ||
| + | id_102 - 1б<br> | ||
Решение и ответ.<br> | Решение и ответ.<br> | ||
<table border=1 cellspacing=10> <tr> <td>1 год<br> | <table border=1 cellspacing=10> <tr> <td>1 год<br> | ||
| Строка 1534: | Строка 1539: | ||
| − | + | [[Категория: Архив проекта ДООМ 2007-2008 (2 цикл)]] | |
| − | [[Категория: | + | |
Текущая версия на 09:00, 22 сентября 2008
Вернуться на главную страницу проекта
Надеемся, вам понравилось решать задачи, которые были подготовлены организаторами олимпиады. Но мы думаем, что у каждого из вас есть интересные задачи по теме олимпиады в вашей копилке, и хотим, чтобы вы поделились ими с нами и с соперниками. Поэтому предлагаем вам принять участие в блиц-конкурсе.
Авторам задач:
- Условие задачи размещается командой в разделе с именем команды (см. ниже) с указанием e-mail команды не позднее 26 марта 2008 года.
- Авторы, разместившие свои задачи в вики-среде, высылают текст задач с решениями на адрес организаторов олимпиады (doom@mec.tgl.ru) не позднее 5 апреля 2008 года.
- Авторы оценивают решения своих задач, присланные соперниками, и результаты оценивания размещают в разделе с именем команды (см. ниже) сразу под условием задачи, а результат оценивания командой своих задач выслают на адрес организаторов олимпиады (doom@mec.tgl.ru) до 12 апреля.
- Авторы задач могут прокомментировать решение своих задач и выставить балл по пятибалльной шкале на странице «Обсуждение» той команды, чье решение они оценивают.
Участникам проекта:
- Решение задач, выложенных в разделе с именем команды (см. ниже), высылаются авторам задач (на указанный e-mail) и организаторам олимпиады (doom@mec.tgl.ru) командами, решившими задачу, до 5 апреля.
- Свой вариант решения задачи команда размещает в разделе с именем команды (см. ниже) под результатами оценивания 14 апреля и 15 апреля 2007 г.
- Отдать свой голос за лучшую задачу можно до 15 апреля на вкладке Обсуждение данной страницы.
Чтобы внести информацию в раздел с именем команды, выполните следующие действия:
- Нажмите ссылку [править] напротив названия своей команды и в поле визуального редактора впишите название своей команды и текст задач (результаты оценивания, решение задач).
- Нажмите кнопку Записать страницу.
Команда 101 "Введите название команды"
Команда 102 "Просто класс"
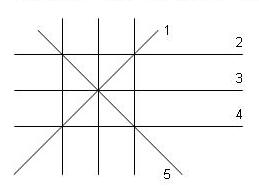
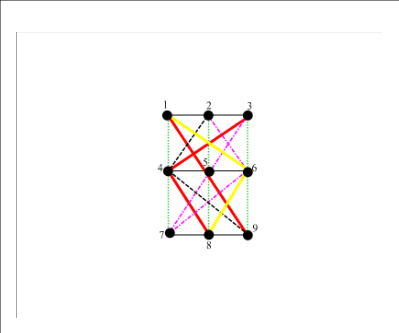
Задача 1. На цирковой арене выступал канатоходец. На высоте 3 метров от земли на 5 столбах были натянуты канаты, по которым он должен был проходить. Канаты были натянуты так, как это показано на рис. 1.
Канатоходец должен был пройти по восьми канатам таким образом, чтобы по каждому из них пройти всего один раз. И это ему всегда удавалось, хотя он и не возвращался в то же место, откуда выходил. Но во время одного из выступлений оборвался канат №8, и осталось всего семь канатов (рис. 2).
Может ли теперь канатоходец пройти все канаты, проходя по каждому из них всего один раз? Покажите, как ходил канатоходец, когда все канаты были целы, и ответьте на поставленный вопрос.
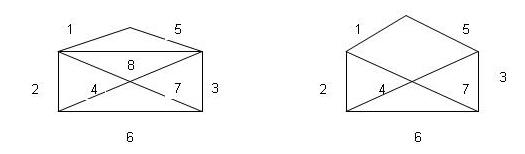
Решение
Оценки:
id_103 - 4
id_109 - 3
id_111 - 5
id_116 - 5
id_122 - 5
id_132 - 4
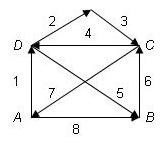
Задача 2. В саду Александра Ивановича тропинки проложены, как это показано на рис. 3, а у Бориса Борисовича - как показано на рис. 4.Кто из них может обойти все свои тропинки, пройдя по каждой всего один раз?

Ответ: Александр Иванович. В его графе все вершины четные
Оценки:
id_109 - 4
id_111 - 5
id_116 - 4
id_122 - 5
id_132 - 5
Задача 3. Садовник имел квадратную клумбу 4x4 м, на которой он выращивал 16 кустов георгинов. Расстояние между кустами составляло 1 м. Пока кусты еще не расцвели, цветовод обходил все кусты, идя по кратчайшему пути, но когда чудесные цветы распустились, садовник обходил их по самому длинному пути. К каждому цветку он подходил только один раз. Как выглядел самый короткий путь от куста к кусту, а как самый длинный?
Решение.
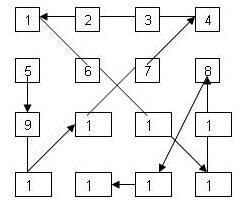
Оценки id_122 - 5
id_132 - 5
Задача 4. В стране 27 городов, каждые два из которых соединены авиалинией. Сколько авиалиний в стране?
Решение351 авиалиния. Каждый город соединен авиалинией с остальными, итого: . Но при таком способе подсчета мы каждую авиалинию считаем дважды
Задача 5. Алеша, Боря и Митя учатся в одном классе. Один ездит домой из школы на автобусе, другой - на трамвае, третий - на троллейбусе. Однажды после уроков Алеша пошел проводить друга до остановки автобуса. Когда мимо них проходил троллейбус, третий друг крикнул из окна: «Боря, ты забыл в школе тетрадь!» Кто на чем ездит домой?
Решение
построим граф, из которого видно, что Алексей ездит со школы домой на трамвае, Витя – на троллейбусе, а Борис – на автобусе. 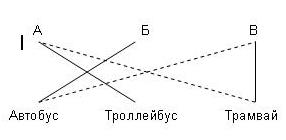
Оценки:
id_103 - 5
id_109 - 5
id_111 - 5
id_120 - 1
id_122 - 5
Задача 6. Начертите каждую из фигур, изображенных на рис. 5, не отрывая карандаша от бумаги и не проводя более раза по одной и той же линии.
Указать признак, по которому можно было заранее судить о том, можно ли нарисовать конкретную фигуру одним росчерком или нет?
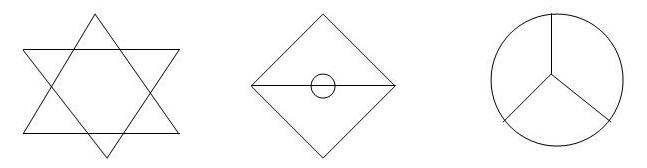
Решение Назовем каждый перекресток, в котором сходятся линии данной фигуры, узлом: четным, если в нем сходится четное число линий, и нечетным, если число сходящихся в нем линий нечетное. Рассмотрим фигуру а, в которой все узлы четные. Начнем свой маршрут из любой точки. Проходя через узел, мы проводим две линии: подводящую к узлу и выводящую из него. Так как из каждого четного узла есть столько же выходов, сколько и входов в него, то по мере продвижения от узла к узлу каждый раз непроведенных линий становится на две меньше, следовательно, принципиально возможно, обойдя их все, вернуться в исходную точку. Фигуру а можно, например, обойти так: A-N-A-G-B-D-F-G-A Фигуру б с двумя нечетными узлами А и В тоже можно начертить одним росчерком. Начнем обход с одного нечетного узла и пройдем по какой-нибудь линии до другого нечетного узла, например, по АСВ. Тем самым мы исключили по одной линии из каждого нечетного узла. В результате оба нечетных узла стали четными, и мы получили оставшуюся фигуру только с четными узлами (треугольник BDA с окружностью), которую, как было показано, можно начертить одним росчерком. Если фигура имеет четыре нечетных узла (таковой является фигура г), то ее можно нарисовать не одним росчерком, а двумя, но это уже не соответствует условию нашей задачи.
Оценки:
id_109 - 5
id_111 - 5
id_116 - 5
id_120 - 5
id_122 - 5
id_132 - 2
Задача 7. В древней рукописи приведено описание города, расположенного на 8 островах. Острова соединены между собой и с
материком мостами. На материк выходят 5 мостов; на 4 островах берут начало по 4 моста, на 3 островах берут начало по 3 моста и на один остров можно пройти только по одному мосту.
Может ли быть такое расположение мостов?
Решение Построим граф и найдем число степени каждой вершины и их сумму. 5+4*4+3*3+1=31 – число нечетное, а по свойству графов число должно быть четное. Значит такого расположения мотсов быть не может.
Оценки
id_111 - 5
id_122 - 5
Задача 8. Учитель математики, проверив контрольные работы у трех
друзей: Алексея, Бориса и Василия, сказал им: «Все вы написали работу, причем получили разные отметки («3», «4», «5»). У Василия — не «5», у Бориса — не «4», а у Алексея,
по моему, «4». Впоследствии оказалось, что учитель ошибся: одному ученику сказал отметку верно, а другим двум неверно. Какие отметки получил каждый из учеников?
Решение
1 случай: верно сказал Алексей. Значит у него 4, значит, Борису и Василию учитель сказал неверно. Получаем, что Борис тоже получил 4, значит этот случай неверный. 2 случай: верно сказали Василию. У него не 5, у Алексея не 4, у Бориса 4, т. е. у Алексея – 5 , у Василия 3. 3 случай: Учитель сказал правду Борису, тогда он получил не 4, Алексей не 4, Василий 5, т. о. 4 никто не получил. Ответ: верное решение – случай 2, Борис – 4, Алексей – 5, Василий – 3.
Оценки:
id_103 - 1
id_111 - 5
id_122 - 5
Задача 9. Три брата — Александр, Борис и Сергей преподают различные предметы в школах Самары, Тольятти и Жигулевска. Александр работает не в Самаре, а Борис не в Тольятти. Самаровец преподает не математику. Тот, кто работает в Тольятти, преподает химию. Борис преподает физику. Какую дисциплину преподает Сергей и в школе какого города?
Решение
сначала определим предмет, который преподают братья
Математика Химия Физика
Самара - -
Тольятти - + -
Жигулевск -
Из таблицы следует, что житель Самары преподает физику, а значит, математику преподает житель Жигулевска. Теперь выясним, как зовут жителей Самары, Тольятти и Жигулевска. Для этого снова воспользуемся таблицей. Так как по условию задачи Борис преподает физику, а из предыдущего рассуждения мы выяснили, что житель Самары преподает физику, то получим, что Борис живет в Самаре.
Александр Борис Сергей
Самара - + -
Тольятти -
Жигулевск -
Больше никаких сведений о зависимости между именем и городом у нас нет. Рассмотрим два возможных случая: 1. Пусть Александр работает в Тольятти. Тогда Сергей будет работать в Жигулевске. 2. Пусть Александр работает в Жигулевске. Тогда Сергей будет работать в Тольятти. Оба случая возможны.
Таким образом, Сергей работает в Жигулевске учителем математики или в Тольятти учителем химии.
Оценки:
id_103 - 5
id_109 - 1
id_111 - 1
id_116 - 5
id_120 - 1
id_122 - 2
Задача 10. Нарисуй 8-мь точек и соедини их отрезками, так чтобы отрезки не пересекались и из каждой точки исходили ровно 4 отрезка .
Решение
Оценки:
id_103 - 1
id_122 - 5
Задача 11. Вдоль прямой дороги стоят 6-ть домов. Где надо вырыть колодец, чтобы сумма расстояний от него до домов была наименьшей.
Решение
Колодец следует строить между третьим и четвертым домом. Чтобы сумма ХА+ХY была наименьшей, точка Х должна находиться на отрезке XY.

Оценки:
id_111 - 2
Задача 12. Коля, Борис, Вова и Юра заняли 4-ре первых места в соревнованиях, причем никакие 2-в мальчика не делили между собой места. На вопрос: « Кто какое место занял?», Коля ответил: « Ни первое, ни четвертое». Боря сказал: « Второе», а Вова заметил, что он был не последний. Кто какое место занял.
Решение
из графа видно, что Вова занял первое место, Боря – второе, Юра – четвертое, а Коля – третье. 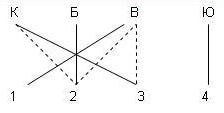
Оценки:
id_111 - 5
id_116 - 5
id_120 - 5
id_122 - 5
Задача 13. 100 город соединены авиалиниями. Доказать, что есть два города, через которые проходит одинаковое число авиалиний.
Решение Т. к. городов всего 100, то авиалиний может быть от 0 до 99, но не может быть, когда один город ни с кем не соединен, а другой соединен со всеми.
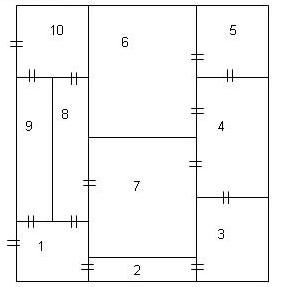
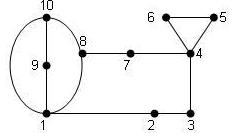
Задача 14. На рисунке привели план подземного лабиринта. Можно ли, начиная из комнат 1. обойти комнаты, так, чтобы пройти все двери комнат, только один раз? В какой комнате закончится обход?
Решение Заменим комнаты точками, а двери – отрезками. Так как у нас два нечетных узла 1 и 5, то данная фигура является уникурсальной. Значит, можно, начиная с одного нечетного узла (1), обойдя все узлы по одному разу, прийти другой нечетный узел (5).
Ответ: можно, закончив обход в комнате 5.
Оценки:
id_111 - 1
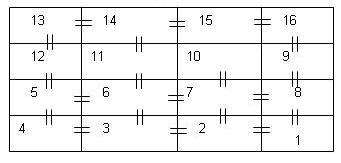
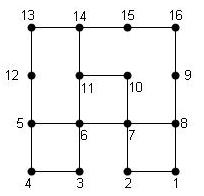
Задача 15. На рисунке изображен план подвала из 10 комнат, можно ли пройти через все двери всех комнат, запирая каждую дверь, через которую проходите? С какой комнаты нужно начать движение?
Решение
Заменяя комнаты точками, а двери – дугами, отрезками, получим фигуру с двумя нечетными узлами 8 и 10, значит, она является уникурсальной, т.е. можно пройти через все двери комнат, запирая каждый раз ту, через которую прошли.
Ответ: можно, начав движение с комнаты 8 или 10.
Оценки:
id_109 - 5
id_111 - 5
Задача 16 Дед рассказал своим внучатам: « В комнате было 5 стульев, на них сидели 4 матери, 4 дочки, 3 бабушки, 2 прабабушки и одна прапрабабушка. Возможно ли это?
Ответ: да, это были дочь, мать, бабушка, прабабушка и прапрабабушка.
Оценки:
id_111 - 5
id_122 - 5
Задача 17 как девять деревьев посадить в восемь рядов, чтобы в каждом ряду было по 3 дерева.
Оценки:
id_109 - 5
id_122 - 5
Задача 18 . Сколько четырехзначных чисел можно составить из чисел 3,4,5,6( цифры в записи не повторяются).
Решение 4*3*2*1=24, так как цифры в числе не повторяются и: на 1-м месте может быть любая из четырех цифр; на 2-м месте может быть любая из оставшихся трех цифр; на 3-м месте – любая из оставшихся двух цифр; На 4-м – оставшаяся цифра.
Оценки:
id_109 - 5
id_120 - 5
id_122 - 5
Задача 19.
Осенний кросс.
Кросс осенний вспоминая,
Спорят белки два часа:
«Победил в забеге заяц,
А второй пришла лиса!»
«Нет, твердит другая белка,-
Ты мне шутки эти брось.
Заяц был вторым, конечно,
Первым был, я помню, - лось!»
«Я, промолвил филин важный,-
В спор чужой не стану лесть.
Но у вас в словах у каждой
По одной ошибке есть».
Белки фыркнули сердито.
Неприятно стало им.
Вы уж, взвесив все, решите,
Кто был первым, кто вторым.
Решение согласно наполовину верным условиям: a) Заяц – I, лиса – II, b) Заяц – II, лось – I. Если Заяц – I, то лиса – не II, тогда заяц – не II и лось – I, следовательно, заяц – не I, а лиса – II. Окончательно получаем: лось – I, лиса – II, заяц – III.
Оценки:
id_103 - 5
id_109 - 5
id_120 - 1
id_122 - 5
Задача 20.
В универмаге встретил я
Осла, козу и кошку,
Они купили красный мяч
И желтую гармошку.
Зайдя потом, увидел я
Осла, козу и белку,
Они купили красный плащ
И белую тарелку.
Зашел я в третий, встретил там
Опять осла и кошку.
Они купили в этот раз
Лишь желтую матрешку.
Мне срочно нужен твой совет,
Задумайся немножко.
Скажи: какой любимый цвет
У белки и у кошки.
И кто не сделал ни одной
Покупки в магазинах.
Поскольку не было, увы,
Товаров ярко-синих.
(Каждый из героев покупает товары одного любимого цвета)
Решение
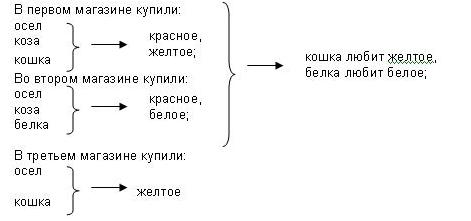
Оценки:
id_103 - 5
id_109 - 4
id_122 - 5
e-mail: mou58@mail.ru
Команда 103 "Перезнайки 103"
Задача №1
Павел Иванович Чичиков побывал у известных вам помещиков по одному разу у каждого. (Герои произведения Гоголя "Мертвые души". Он посещал их в следюющем порядке: Манилова, Коробочку, Ноздрева, Собакевича, Плюшкина, Тентетникова, генерала Бетрищева, Констанжогло, полковника Кошкарева. Найдена схема на которой Чичиков набросал взаимное расположение имений и проселочных дорог, соединяющих их. Установите, какое имение кому принадлежит, если ни по одной из дорог Чичиков не проезжал более одного раза.
Задача №2
На рисунке изображен план подземелья, в одной из комнат которого скрыты богатства рыцаря. После смерти рыцаря его наследники нашли завещание, в котором было сказано, что для отыскания сокровищ достаточно войти в одну из крайних комнат подземелья, пройти через все двери, причем в точности по одному разу через каждую; сокровища скрыты за той дверью, которая будет пройдена последней. В какой комнате были скрыты сокровища?
Задача №3
У Аси есть любимый костюм, в котором она ходит в школу.Она одевает к нему белую, голубую, розовую или красную блузку. А в качестве "сменки" берёт босоножки или туфли. Кроме того у Аси есть 3 разных бантика (№1,№2,№3), подходящих ко всем блузкам. Сколько дней она будет ходить в красной блузке и босоножках?
e-mail: Почтовый ящик нашей команды, ждём писем
Команда 104 "Проводники по графикам"
===Задача о трех домах и трех колодцах===
Имеется три дома и три колодца, каким-то образом расположенные на плоскости. Провести от каждого дома к каждому колодцу тропинку так, чтобы тропинки не пересекались.
===Задача о четырех красках===
Разбиение на плоскости на непересекающиеся области называется картой. Области на карте называются соседними, если они имеют общую границу. Задача состоит в раскрашивании карты таким образом, чтобы никакие две соседние области не были закрашены одним цветом.
===Задача о планетах===
Между девятью планетами солнечной системы установлено космическое сообщение. Рейсовые ракеты летают по следующим маршрутам: Земля – Меркурий; Плутон – Венера; Земля – Плутон; Плутон – Меркурий; Меркурий – Вене; Уран – Нептун; Нептун – Сатурн; Сатурн – Юпитер; Юпитер – Марс и Марс – Уран. Можно ли долететь на рейсовых ракетах с Земли до Марса?
===Задача о телефонах===
В городе Маленьком 15 телефонов. Можно ли их соединить проводами так, чтобы каждый телефон был соединен ровно с пятью другими?
===Волшебная задача===
В Тридевятом царстве только один вид транспорта – ковер-самолет. Из столицы выходит 21 ковролиния, из города Дальний – одна, а из всех остальных городов, – по 20. Докажите, что из столицы можно долететь в город Дальний.
e-mail: school61@edu.tgl.ru
Команда 105 "Введите название команды"
Команда 106 "Введите название команды"
Команда 107 "Введите название команды"
Команда 108 "Введите название команды"
Команда 109 "ГРАФ"
Задача 1.
На острове живут рыцари, которые всегда говорят правду , и лжецы, которые всегда лгут. Путник встретил троих островитян и спросил каждого из них: «Сколько рыцарей среди твоих спутников?». Первый ответил: «Ни одного». Второй сказал: «Один». Что сказал третий?
Решение:
Ответ: один. Если первый- рыцарь, то в сил его слов второй и третий – лжецы. Что невозможно из-за высказывания второго островитянина. Значит, первый- лжец. Если второй- лжец, то в силу его слов третий тоже лжец, но тогда первый сказал правду, а он должен был соврать. Значит, второй- рыцарь. В силу его слов третий тоже рыцарь. Третий честно ответит: «Один»
Оценки:
id_102-4
id_110-1
id_122-0
Задача 2.
Сколько 3х- значных чисел можно составить из цифр 1,3,5,7. используя в записи числа каждую из них не более одного раза?
Решение:
Строим дерево. При условии, что на первом месте в числе будет стоять цифра 1, можно будет составить 6 чисел, если на первом месте будут стоять цифры 3,5,7. 4 * 3 *2 = 24 Ответ: 24
Оценки:
id_102-4
id_110-5
id_122-5
Команда 110 "Умники"
Задача №1
1) В бригаде строителей было 5 человек: Андреев, Борисов, Иванов, Петров, Сидоров. Профессии у них были разные: один из них маляр, другой—плотник, третий—штукатур, четвёртый—каменщик, пятый—электрик. Они рассказали о себе следующее.
Петров и Иванов никогда не держали в руках малярной кисти. Петров и Борисов живут в одном доме со штукатуром. Андреев и Петров подарили электрику красивую вазу. Борисов и Петров помогали плотнику строить гараж. Борисов и Сидоров по субботам встречаются у электрика, а штукатур по воскресеньям приходит в гости к Андрееву. У кого из них какая профессия?
Ответ: Борисов- маляр, Андреев- плотник, Иванов- электрик, Петров- каменщик, Сидоров- штукатур.
Задача №2
2) Смит, Джонс и Робинсон работают в одной поездной бригаде машинистом, кондуктором и кочегаром. Профессии их названы не обязательно в том же порядке, что и фамилии. В поезде, который обслуживает бригада, едут трое пассажиров с теми же фамилиями. В дальнейшем каждого пассажира мы будем почтительно называть «мистер» (м-р)
2. М-р Робинсон живет в Лос-Анджелесе.
3. Кондуктор живет в Омахе.
4. М-р Джонс давно позабыл всю алгебру, которой его учили в колледже.
5. Пассажир – однофамилец кондуктора живет в Чикаго.
6. Кондуктор и один из пассажиров, известный специалист по математической физике, хотя в одну церковь.
7. Смит всегда выигрывает у кочегара, когда им случается встречаться за партией в бильярд. Как фамилия машиниста?
Ответ: Смит-машинист.
Задача №3
3). В одном городе живёт 5 человек. Их имена Леонид, Михаил, Николай, Олег, и Пётр. Их фамилии Атаров, Бартенев, Кленов, Данидин и Иванов.
Бартенев знаком только с двумя из перечисленных мужчин.
Пётр знаком со всеми, кроме одного.
Леонид знает только одного из всех. Данилин и Михаил незнакомы. Николай и Иванов не знают друг друга.
Михаил, Николай и Олег знакомы между собой. Атаров незнаком только с одним из всех. Только один из всех знаком с Кленовым.
Назовите имена и фамилии каждого. С кем знаком каждый из них?
Решение: Леонид, который знаком только с одним из остальных мужчин, не может ни Бартеневым, ни Атаровым. Петр не может быть Бартеневым так как Петр знаком с тремя мужчинами. Очевидно что Данилин—не Михаил и Николай — не Иванов. Поскольку у Кленова лишь один знакомый, он не может быть ни Михаилом, ни Николаем, ни Олегом, так как вся эта "троица" знакома между собой. Учитывая, что член "троицы" Михаил не знаком с Данилиным, можно сделать вывод, что Данилин - не Олег и не Николай. Как уже установлено, Кленов может быть либо Петром, либо Леонидом. Но Пётр знаком со всеми, кроме одного, а нам известно, что Кленова знает только один из всех. Следовательно, имя Кленова Леонид. Теперь ясно, что Данилин - Петр, так как все остальные варианты уже отпали. Можно сделать чертёж. Соединим прямыми линиями те пары точек, которые соответствуют людям, знакомым друг с другом. Нетрудно также сделать вывод, что с Кленовым знаком Данилин. Легко видеть, что с двумя мужчинами знаком только Михаил. Следовательно, его фамилия—Бартенев. Теперь нетрудно сделать вывод, что Атаров — Николай, а Иванов - Олег. Кленов знаком только с Данилиным. Данилин знаком с Кленовым, Атаровым и Ивановым, Бартенев знаком с Атаровым н Ивановым, Иванов знаком с Бартеневым, Данилиным и Атаровым, а Атаров — с Данилиным, Бартеневым и Ивановым.
Ответ: Кленов знаком только с Данилиным. Данилин знаком с Кленовым, Атаровым и Ивановым, Бартенев знаком с Атаровым н Ивановым, Иванов знаком с Бартеневым, Данилиным и Атаровым, а Атаров — с Данилиным, Бартеневым и Ивановым.
E-mail: polyakova@other.omsu.omskreg.ru или
mou062@omsk.edu.ru
ОЦЕНКИ
id_113 3
id_114 4
id_ 120 3
id_122 4
Команда 111 "Лемниската"
Головоломка 1.
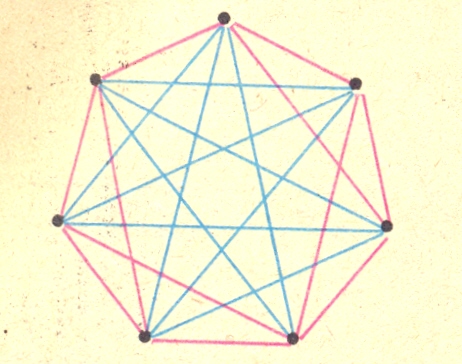
Нарисуйте полный граф с семью вершинами. Можно ли раскрасить этот граф двумя цветами (красным и синим) так, чтобы не получилось синих треугольников и получилось не более четырех красных треугольников?
id 132 - 0
Решение:
Головоломка 2.
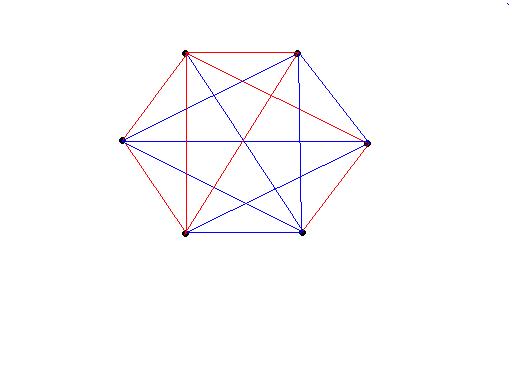
Докажите, что в любой компании из шести человек найдутся трое людей либо попарно знакомых, либо попарно абсолютно незнакомых.
id 102 - 2
id 132 - 4
Решение
Эту головоломку легко преобразовать в задачу о графах. Шесть вершин соответствуют шести людям. Соединим пару вершин, соответствующих двум знакомым людям, красной линией, а пару вершин, соответствующих двум незнакомым людям, синей линией. Как бы мы ни выбирали цвета линий, у нас неизбежно получится или красный треугольник (соответствущий тройке попарно знакомых), или синий треугольник (соответствующий тройке попарно незнакомых).
E-mail команды: shuric_80@mail.ru
Команда 112 "Введите название команды"
Команда 113 "Графство кривых зеркал"
Задача 1. Полет дирижабля
Из Ленинграда вылетел прямо на север дирижабль. Пролетев в северном направлении 500км, он повернул на восток. Пролетев в эту сторону 500км, дирижабль сделал новый поворот - на юг и прошел в южном направлении 500км. Затем он повернул на запад и, пролетев 500км, опустился на землю. Спрашивается: где расположено место спуска дирижабля относительно Ленинграда - к западу, к востоку, к северу или к югу?
id_122 - 0б
id_102 - 0б
Решение.
На первый взгляд можно подумать, что задача содержит противоречие. Но дирижабль летел не по контуру квадрата, а по шарообразной форме Земли. Медианы к северу сближаются, поэтому, пройдя 500км по параллельному кругу, расположенному на 500 км севернее широты Ленинграда, дирижабль отошел к востоку на большее число градусов, чем пролетел потом в обратном направлении. В результате дирижабль, закончив полет, оказался восточнее Ленинграда.
Ответ: место спуска дирижабля относительно Ленинграда расположено к востоку
Задача 2.
Барсук позвал к себе гостей:
Медведя, рысь и белку,
И подарили барсуку
Подсвечник и тарелку.
Когда же он позвал к себе
Рысь, белку, мышку, волка,
То он в подарок получил
Подсвечник и иголку.
Им были вновь приглашены
Волк, мышка и овечка,
И получил в подарок он
Иголку и колечко.
Он снова пригласил овцу,
Медведя, волка, белку,
И подарили барсуку,
Колечко и тарелку.
Нам срочно нужен ваш совет
(На миг дела отбросьте):
Хотим понять, какой предмет
Каким дарился гостем.
И кто из шестерых гостей
Явился без подарка?
Не можем мы сообразить,
Сидим...Мудрим...Запарка!
id_122 - 3б
id_114 - 4б
id_120 - 3б
Решение и ответ.
Представим схематически условие задачи:  Из 1) и 2), получаем, что медведь подарил тарелку, а подсвечник подарила рысь или белка. Добавляем условие 4), получаем, что подсвечник подарила рысь.
Из 2) видно, что иголку подарила мышка или волк, но из 4) заключаем, что волк иголку не дарил, значит, иголку подарила мышка. Из 3) получаем, что колечко подарила овечка,
Из 1) и 2), получаем, что медведь подарил тарелку, а подсвечник подарила рысь или белка. Добавляем условие 4), получаем, что подсвечник подарила рысь.
Из 2) видно, что иголку подарила мышка или волк, но из 4) заключаем, что волк иголку не дарил, значит, иголку подарила мышка. Из 3) получаем, что колечко подарила овечка,
в результате имеем: медведь подарил тарелку, рысь – подсвечник, мышка – иголку, овечка – колечко, а без подарка явились волк и белка.
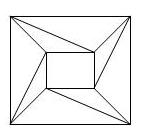
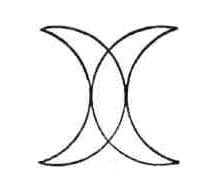
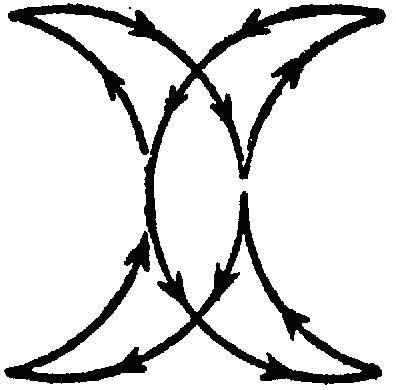
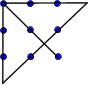
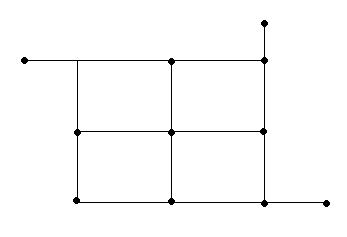
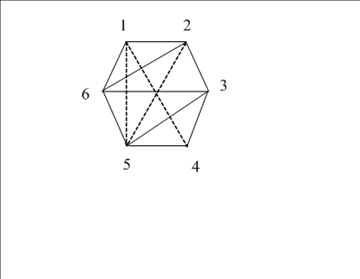
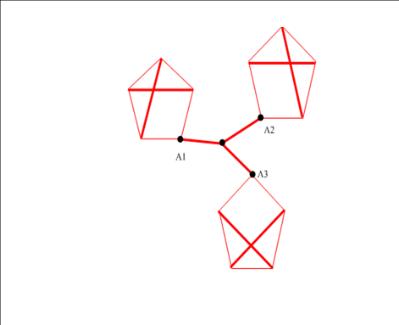
Задача 3.
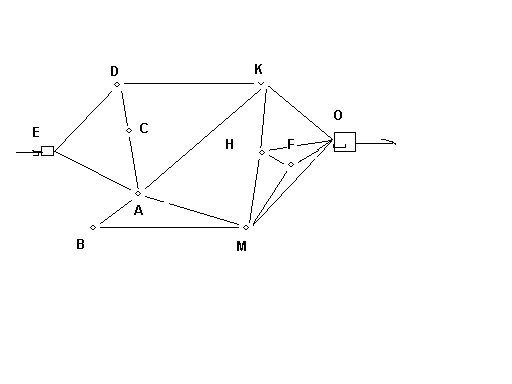
Можно ли начертить данную фигуру одним росчерком?
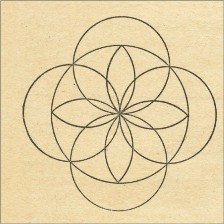
id_122 - 5б
id_120 - 5б
id_102 - 5б
Решение.
Можно начертить данную фигуру, т.к. если пересечения линий обозначить вершинами, то все они четные, значит, по закономерности можно начертить данную фигуру одним росчерком пера.
Задача 4. Музыкальные инструменты и иностранные языки
Каждая из трех девушек - Анна, Галина, Виктория и Светлана - умеет играть только на одном музыкальном инструменте и знает только один иностранный язык. Анна играет на виолончеле. Говорящая по-французски играет на скрипке. Светлана не органистка. Виктория не говорит по-немецки. Анна не знает итальянского языка. Галина не играет на скрипке и не говорит по-английски. Светлана не знает французского. Виктория не арфистка. Органистка не говорит по-итальянски. Какой язык знает и на каком инструменте играет Светлана?
id_122 - 5б
id_114 - 5б
id_120 - 5б
id_102 - 1б
Решение.
Нарисуем граф с вершинами и, ф, н, а – название языков, с, а, о, в – название инструментов, Анна, Галина, Виктория, Светлана – имена девушек.
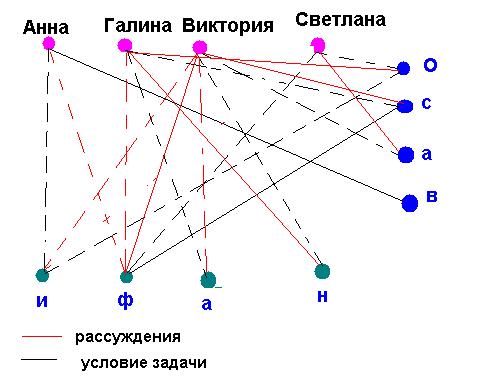
Укажем на нем условия задачи. По условию задачи Анна играет на виолончели. Из него видно, что Галина не играет на скрипке, значит, она не знает французского языка. Т.к. говорящая по-французски играет на скрипке, то Анна не говорит на этом языке. Значит, по-французски говорит Виктория, а, следовательно, играет на скрипке. Тогда Светлана являясь не органисткой, играет на арфе. А Галина получается орфистка, не говорящая по-итальянски и не знает английского, значит, она говорит по-немецки. Анне остается английский язык, а Светлане итальянский.
Ответ: Светлана говорит по-итальянски и играет на арфе
Задача 5.
В конструкторском бюро работают Антонов, Борисов, Кириллов и Дроздов. Все хотят отдыхать летом, и поэтому при составлении графика отпусков всегда возникают бесконечные споры. Попробуйте помочь составить график отпусков на 4 года, который бы удовлетворял следующим пожеланиям сотрудников:
1) в отпуск сотрудники хотят идти только с мая по август;
2) продолжительность отпуска - один месяц;
3) в каждом месяце в отпуск может пойти только один человек;
4) за четыре года каждый из четырех сотрудников должен получить отпуск по одному разу в каждом из трех месяцев;
5) в первый год Кириллов хочет отдыхать в июле;
6) во второй год Антонову отпуск нужен в мае;
7) в третий год Дроздову отпуск нужен в июне;
8) Борисов на четвертый год предполагает уйти в отпуск в июле;
9) в августе все хотят отдыхать следующим образом: в первый год-Дроздов, во второй-Кириллов, в третий-Борисов, в четвертый-Антонов.
id_122 - 5б
id_114 - 5б
id_103 - 5б
id_102 - 1б
Решение и ответ.
| 1 год Май - Борисов |
2 год |
3 год |
4 год |
Условие задачи помечено курсивом, полужирный – рассуждения. Т.к. Антонов был в мае на 2 год, то на первый он будет в июне, Борисову достается май. Антонов в 3 год получается идет в отпуск в июле, а Кириллову достается май в этот год. Кириллову достается в 4 год июнь, а Дроздову май. Во 2 год Дроздову достается июль, а Борисову – июнь.
Ждем ответы по адресу: doom_school41@mail.ru
Команда 114 "Тандем"
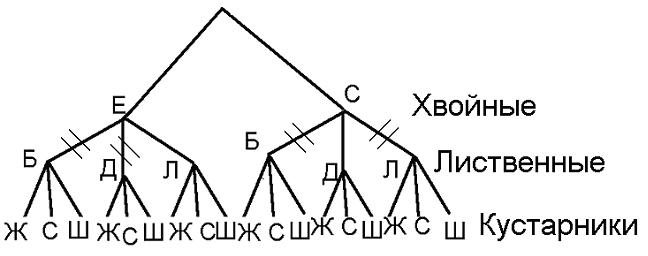
Задача 1. Для озеленения района по плану архитектора нужно посадить аллею зеленых саженцев, чередуя хвойные, лиственные деревья и кустарник. Были предложены три группы растений. В первую группу входят хвойные деревья: ель и сосна, во вторую группу – лиственные деревья: берёза, дуб, липа; в третью группу – кустарники: жасмин, сирень, шиповник. Найдите все варианты озеленения, если известно, что дуб плохо влияет на рост жасмина и сирени, липа – на рост шиповника. Несовместимы: сосна и берёза, сосна и липа, ель и дуб, ель и берёза.
ОТВЕТ: 3 варианта: 1) Ель – липа – жасмин; 2) Ель – липа – сирень; 3) Сосна – дуб шиповник.
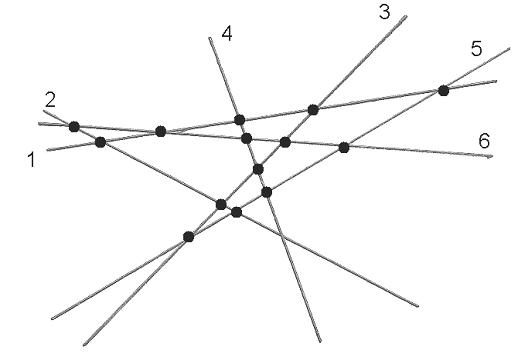
Задача 2. На плоскости нужно нарисовать 6 различных прямых. Какое наибольшее число пересечений этих прямых возможно?
Оценки:
id_113 - 3 балла,
id_122 - 5 баллов.
Решение:
ОТВЕТ: 15
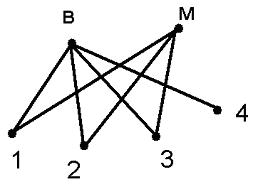
Задача 3. В шахматном турнире по круговой системе, в котором участвуют 6 школьников, сыграно 10 партий. Известно, что каждый участник сыграл не менее двух встреч, Ваня провел 4 встречи, а Миша – 3. Сыграл ли ещё кто-нибудь, кроме Вани, больше, чем Миша, если Ваня и Миша между собой не встречались?
Оценки:
id_102 - 0 баллов.
Решение:
Построим граф, показывающий встречи Вани и Миши:
Нужно провести еще 3 ребра, соединяющих некоторые пары, помеченных числами 1, 2, 3,4. В каждом из случаев проведения этих ребер появится вершина, из которой будет выходить 4 ребра.
ОТВЕТ: существует участник, кроме Вани, который провел больше встреч, чем Миша.
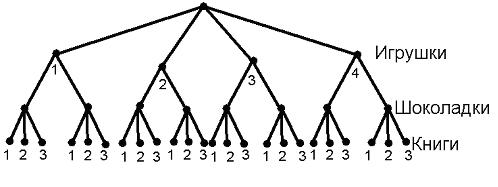
Задача 4. В новогодний подарок для первоклассника входит одна игрушка, одна шоколадка и одна книжка. Для формирования подарков купили игрушки четырёх видов, шоколадки двух сортов и книги трех авторов. В классе 25 учеников. Докажите, что хотя бы двое из них получат одинаковые подарки.
Оценки:
id_113 - 5 баллов,
id_102 - 5 баллов,
id_122 - 5 баллов.
Решение:
Процесс формирования подарков можно изобразить деревом:
Получили 24 различных варианта различных подарков. Но в классе 25 учеников. Поэтому хотя бы одна пара должна получить одинаковые подарки.
Задача 5. В небольшой роще находится заяц. Выскочив из норы и бегая от дерева к дереву, он оставил следы и, наконец, спрятался под деревом. (рис.1).
Опытный охотник определил, что между каждыми двумя деревьями заяц пробегал не более раза. Под каким деревом находится нора зайца, и где сейчас он спрятался?
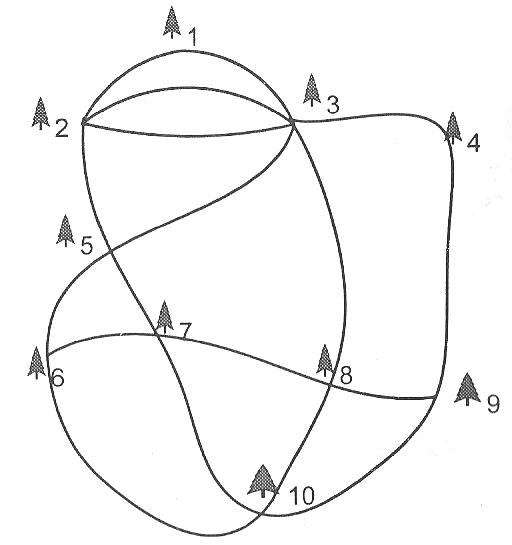
Оценки:
id_113 - 5 баллов,
id_120 - 5 баллов,
id_102 - 4 балла,
id_122 - 0 баллов.
Решение:
Будем считать каждое дерево вершиной графа, а путь зайца от дерева к дереву – ребром графа. Все вершины этого графа имеют четную степень. Значит, нора зайца находится под деревом, обозначенным цифрой 6, а сам заяц под деревом, обозначенным цифрой 9, или наоборот.
ОТВЕТ: Задача имеет два решения.
E-mail команды: kta-08@yandex.ru
Команда 115 "Введите название команды"
Команда 116 "Умницы и умники"
1. Сергеев, Панин, Борисов и Леднев соревновались на звание лучшего рыболова. Но ведь рыба рыбе - рознь. Поэтому договорились оценивать каждую рыбу по-разному: поймал судака - получай 5 очков, за леща - 4, за окуня - 2, за ерша - 1. Единственного судака поймал Сергеев. Было выловлено 3 окуня. Все рыбаки вместе набрали 18 очков. Меньше всего очков заработал Панин, хотя и наловил рыбы больше всех. Панин и Борисов вместе набрали очков столько же, сколько Сергеев и Леднев. И наконец, все набрали разное количество очков. Определите улов каждого рыбака.
2. Ваня живет выше Сени, Сеня - ниже Наташи. Кто живет выше - Наташа или Ваня?
3. Сколько треугольников, прямоугольников, квадратов на рисунке?
Решения присылать по адресу: doom2_school41@mail.ru
Команда 117 "Введите название команды"
Команда 118 "Введите название команды"
Команда 120 "ГРАФиТЫ"
Решите с помощью графа.
ЗАДАЧА 1.
В купе одного из вагонов поезда Москва – Одесса ехали москвич, ленинградец, туляк, киевлянин, харьковчанин и одессит. Их фамилии начинались буквами А, Б, В, Г, Д и Е.
В дороге выяснилось, что А и москвич – врачи; Д и ленинградец – учителя, а туляк и В – инженеры. Б и Е – участники Отечественной войны, а туляк в армии совсем не служил. Харьковчанин старше А, одессит старше В. Б и москвич сошли в Киеве, а В и харьковчанин в Виннице. Определите профессию каждого из этих шести пассажиров и место жительства каждого из них.
П р и м е ч а н и е. Не лишен интереса вопрос о необходимости и достаточности количества фактов, устанавливаемых условием этой задачи. Может быть заинтересуетесь этим небольшим исследованием?
Комментарии. Ни одна команда пока не ответила на вопрос о необходимости и достаточности количества фактов.
Таким образом,
Тандем_114 - 4 балла (нет решения)
Граф_109 - 2 балла (не опредили место жтельства каждого пассажира)
Пентаграма_122 - 4+ балла. Молодцы, подробное решение задачи.
Решение: Задачи такого рода решаются методом исключения. Перечислим факты, содержащиеся в условии: 1) А и москвич – врачи. 2) Д и ленинградец – учителя. 3) В и туляк – инженеры. 4) Б и Е – участники Отечественной войны, а туляк в армии не служил. 5) Харьковчанин старше А. 6) Одессит старше В. 7) Б и москвич сошли в Киеве. 8) В и харьковчанин сошли в Виннице. Из этих фактов, как логические следствия, выявляются скрытые факты. Например, из фактов (1) и (2) следует, что А – не москвич (1), но А – и не ленинградец (1-2); Д – не ленинградец (2), но Д – и не москвич (1-2) и т.п. Построим граф. Итак, А не москвич и не ленинградец; Д не ленинградец и не москвич; В не туляк, не москвич и не ленинградец (условие 1, 2 3); А не туляк (условие3); Д не туляк (условие 3); Б не туляк (условие 4); Е не туляк (условие 4);
Следовательно, Г – туляк.
А не харьковчанин (условие 5); В не одессит (условие 6); Б не москвич (условие 7);
Следовательно, Е – москвич.
В – не харьковчанин (условие 8).
Следовательно, В – киевлянин.
Из графа видим,
Что Б – ленинградец,
А – одессит,
Д – харьковчанин.
Теперь легко определяются и специальности пассажиров: А и Е врачи, Б и Д – учителя, В и Г – инженеры.
Всего из условия задачи было почерпнуто 17 фактов. Достаточность этого количества фактов следует из того, что зада все-таки решена и в процессе решения не было никаких противоречий. Но все ли 17 фактов являются необходимыми для решения задачи? Очевидно – нет, так как два факта, например, подтверждают. Что В – не москвич. Какое же количество фактов является необходимым? Так как каждый пассажир является жителем одного из городов, то для установления методом исключения местожительства первого пассажира необходимо 5 фактов, указывающих, в каких пяти городах он не живет. После этого, для установления местожительства второго пассажира достаточно располагать только четырьмя фактами того же типа и т.п. Всего, следовательно, для наиболее экономичного построения задачи о шести пассажирах и для её решения необходимо и достаточно иметь 5+4+3+2+1=15 фактов указанного типа. В этой задаче два факта лишние. Ответ: А – одессит, Б – ленинградец, В – киевлянин, Г – туляк. Д – харьковчанин, Е – москвич. А и Е – врачи, Б и Д – учителя, В и Г – инженеры.
ЗАДАЧА 2.
Десять мальчиков: Александр, Борис, Василий, Георгий, Дмитрий, Евгений, Захар, Иван, Кирилл и Леонид – учатся все в разных классах одной десятилетней школы.
1) Старший брат Дмитрия оканчивает 7-ой класс, а младший брат Евгения учится в 5-ом классе. Александр старше Кирилла на один класс, а Леонид старше Евгения на два класса.
2) Василий не оканчивает школу в этом году. Иван при окончании 4-го класса получил похвальную грамоту. Борис – пионервожатый в 5-ом классе, а Василий в 4-ом классе.
3) Александр, Кирилл и шестиклассник занимаются в гимнастической секции, а одновременно с ними тренируются баскетболисты, среди которых всегда Борис, Евгений и восьмиклассник.
4) Александр и семиклассник живут на улице Ленина, Георгий и пятиклассник – на улице Куйбышева, Дмитрий, первоклассник и восьмиклассник – на Садовой, а Кирилл и десятиклассник – На Октябрьской.
5) Борис помогает в учёбе Евгению, Дмитрий – Ивану, Георгий – Александру.
Кто из них в каком классе учится?
Комментарии.Наша олимпиада называется "Тайна графов". Здесь мы учимся решать задачи с помощью графов. Но есть ещё один способ решения логических задач: спомощью, так называемой, таблицы истинности. Именно этим способом и воспользовались командЫ Пентаграмма_122 и Тандем_114. Мы согласны, что данную задачу легче решить именно так.
Тандем_114 - 5 баллов.
Пентаграмма_122 - 5+ баллов.
Граф_109 - 3 балла (нет решения)
Ответ: В 1 классе – Захар, во 2 классе – Кирилл, в 3 классе – Александр, в 4 классе – Григорий, в 5 классе – Иван, в 6 классе – Дмитрий, в 7 классе – Евгений, в 8 классе – Василий, в 9 классе – Леонид, в 10 классе – Борис.
Изобразите одним "росчерком пера".
ЗАДАЧА 3.
Комментарии.Уважаемые соперники, команда Перезнайки_103 и команда МОУ 58. Вопрос задачи №3 и №4 не звучит "можно или нельзя",. Условие задачи четко сформулировано "Изобразите...".
Пентаграмма_122 - 5 баллов.
Граф_109 - 5 баллов.
ЗАДАЧА 4.
Тандем_114 - 5 баллов.
Пентаграмма_122 - 5 баллов.
Граф_109 - 5 баллов.
E-mail: komanda8800@mail.ru
Команда 121 "Введите название команды"
Команда 122 "Пентаграмма"
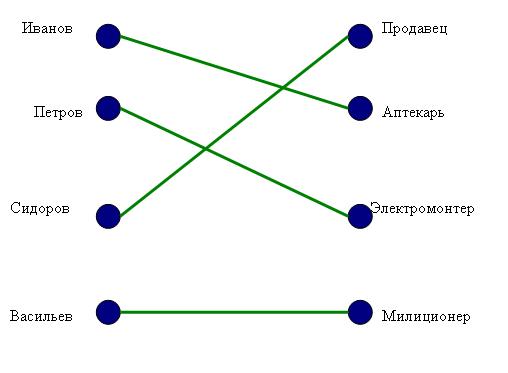
Задача1. Иванов, Петров, Сидоров и Васильев живут в одном городе. Их профессии - продавец, аптекарь, электромонтер и милиционер. Иванов и Петров - соседи и всегда на работу ездят вместе. Петров старше Сидорова. Иванов обыгрывает Васильева в домино. Продавец ходит на работу пешком. Милиционер не живет рядом с аптекарем. Электромонтер и милиционер встречались единственный раз, когда милиционер задержал электромонтера за нарушение правил уличного движения. Милиционер старше аптекаря и электромонтера. Кто чем занимается?
Решение:
Ответ: Иванов – аптекарь, Петров – электромонтер, Сидоров – продавец, Васильев – милиционер.
Оценки: ID_120 - 5б
ID_113 - 4б (хотелось бы увидеть графы в ваших решениях)
ID_132 - задача решена на 4 б, но решение было прислано не 5, а 7 апреля (просим организаторов проекта рассмотреть вопрос о начислении балов )
Задача 2. В отделении Сбербанка работают: кассир, контролер и заведующий. Их фамилии: Борисов, Иванов и Сидоров. Кассир не имеет ни братьев, ни сестер и меньше всех ростом. Сидоров женат на сестре Борисова и ростом выше контролера. Назовите фамилии кассира, контролера и заведующего.
Решение:
Сидоров не кассир и не контролер, значит, он заведующий. Борисов не кассир. Тогда он может быть только контролером. А Иванов - кассир.
Ответ: Сидоров - заведующий, Иванов - кассир, Борисов - контролер.
Оценки:
ID_120 - 5б
ID_102 - 2б (ответ верный, но не было предложено ни рассуждений, ни графа)
ID_132 - задача решена на 4 б, но решение было прислано не 5, а 7 апреля (просим организаторов проекта рассмотреть вопрос о начислении балов )
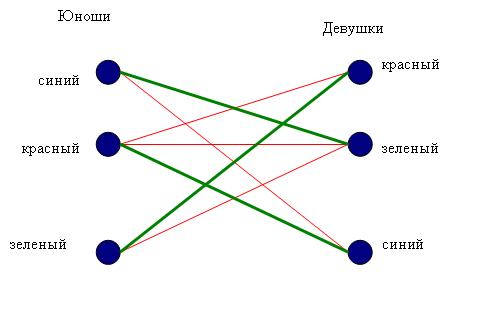
Задача 3. На школьном вечере танцевали три пары. Юноши, как и девушки, были одеты в костюмы разных цветов: красный, зеленый и синий. Оказавшись в один из моментов рядом с девушкой в зеленом, юноша в красном обратился к ней: "Неправда ли, забавно получается: ни у кого из нас цвет костюма не совпадает с цветом костюма партнера". В костюме какого цвета был юноша, танцевавший в паре с девушкой в красном?
Ответ: С девушкой в красном танцует юноша в зеленом.
Оценки:
ID_120 - 5б
ID_113 - 4б
ID_102 - 0б
ID_132 - задача решена на 4 б, но решение было прислано не 5, а 7 апреля (просим организаторов проекта рассмотреть вопрос о начислении балов )
Задача 4. В пруд запустили 30 щук, которые постепенно поедают друг друга. Щука считается сытой, если она съела трех щук (сытых или голодных). Какое наибольшее число щук может насытиться?
Решение:7 щук съедят по три голодных щуки. оставшиеся две съедят по 3 ранее насытившихся.
Ответ: насытиться могут 9 щук.
Оценки:
ID_113 - 5б
ID_102 - 0б
ID_132 - 0б
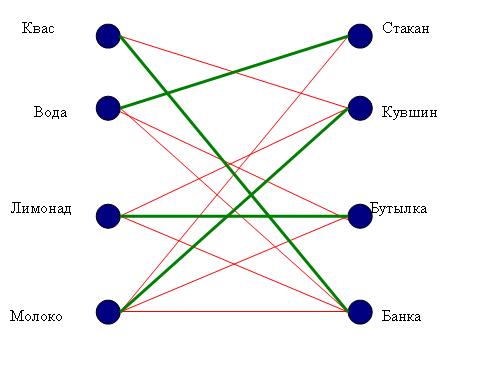
Задача 5. В бутылке, стакане, кувшине и банке находятся молоко, лимонад, квас и вода. Известно, что вода и молоко не в бутылке, сосуд с лимонадом стоит между кувшином и сосудом с квасом, в банке не лимонад и не вода. Стакан стоит около банки и сосуда с молоком. Где находится квас?
Решение:
Из графа видно, что квас в банке, лимонад в бутылке, вода в стакане, молоко в стакане.
Ответ: Квас в банке.
Оценки:
ID_120 - 5б
ID_113 - 4б
ID_102 - 2б (ответ верный, решения нет)
ID_132 - задача решена на 2 б, но решение было прислано не 5, а 7 апреля (просим организаторов проекта рассмотреть вопрос о начислении балов )
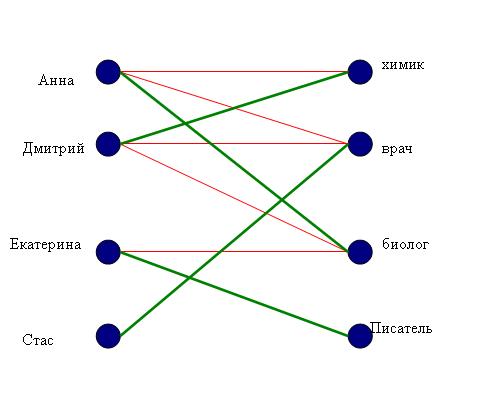
Задача 6. На деловой встрече были писатель, химик, биолог и врач. Их звали (по алфавиту): Анна, Дмитрий, Екатерина и Стас. Дмитрий сказал биологу, что только что встретил Екатерину с пончиками. Анна сидела напротив врача и рядом с химиком. Врач про себя размышлял о том, что Стас - глупое имя. Назовите специальность каждого.
Решение:Так как Дмитрий говорил с биологом о Екатерине, а Анна сидела рядом с химиком и напротив врача, то Дмитрий и Екатерина не могут быть биологом. А Анна не может быть химиком и врачом. Поскольку врач никому ничего не говорил, а Дмитрий говорил, то Дмитрий не может быть врачом. Врачом был Стас, поскольку он размышлял о собственном имени. Методом исключения возможностей получаем, что биологом была Анна. Так как Екатерина ходила за пончиками, а Анна сидела рядом с врачом и химиком, то Екатерина не может быть химиком. Значит, Екатерина - писатель, а Дмитрий - химик.
Ответ: Стас - врач, Дмитрий - химик, Екатерина - писатель, Анна - биолог.
Оценки:
ID_102 - 2б(нет решения)
ID_132 - задача решена на 1 б, но решение было прислано не 5, а 7 апреля (просим организаторов проекта рассмотреть вопрос о начислении балов )
Задача 7. Соединить все точки на рисунке 4-мя отрезками.
. . .
. . .
. . .
Решение:
Оценки:
ID_132 - задача решена на 5 б, но решение было прислано не 5, а 7 апреля (просим организаторов проекта рассмотреть вопрос о начислении балов )
Задача 8. В конторе работают 4 бухгалтера: Иванов, Борисов, Сидоров и Демин. Один из них женат на сестре одного из своих сослуживцев. Имена жен: Анна, Валя, Соня и Дина. У Демина сестер нет. Жену Борисова зовут Валя. Жена Сидорова вместе с Анной и Диной ходит на шейпинг. Сестра жены Иванова замужем за Сидоровым. Кто брат Сони?
Решение:
Жена Сидорова – не Валя (т.к. она жена Борисова), не Анна и не Дина (т.к. с ними она ходит на шейпинг). Значит, Сидоров женат на Соне. Соня – сестра жены Иванова, тогда Иванов – не брат Сони. Брат Сони – не Иванов, не Сидоров, не Демин, т.е. брат Сони – Борисов.
Ответ: Борисов.
Оценки:
ID_132 - задача решена на 3 б, но решение было прислано не 5, а 7 апреля (просим организаторов проекта рассмотреть вопрос о начислении балов )
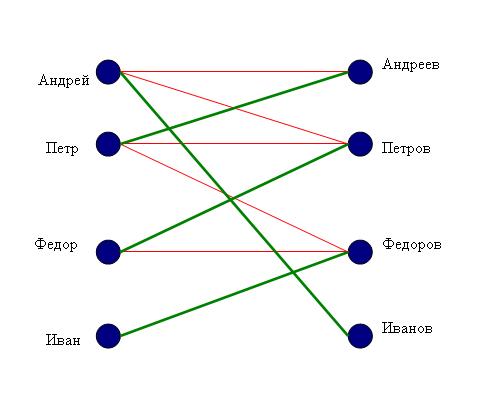
Задача 9. Четыре школьника, имена которых Андрей, Пётр, Иван и Фёдор, имели фамилии Андреев, Петров, Иванов и Фёдоров. Но ни у одного из них собственные имя и фамилия не были одинаковыми.
Требуется определить фамилию каждого из школьников, если известно следующее:
1. У Ивана фамилия не Андреев.
2. Имя школьника с фамилией Фёдоров - фамилия (почти) того школьника, чье имя фамилия Петра.
Ответ:Андрей Иванов, Пётр Андреев, Иван Фёдоров и Фёдор Петров
Оценки:
ID_132 - задача решена на 5 б, но решение было прислано не 5, а 7 апреля (просим организаторов проекта рассмотреть вопрос о начислении балов )
Задача 10. Восемь коллег на прощание жмут друг другу руки. Сколько всего предстоит рукопожатий?
Решение:Можно построить полный граф, у которого будет 8 вершин и посчитать количество ребер.
Другой способ : Первый уходящий жмет руку семи работникам, второй – шести, третий – пяти, четвертый – четырем, третий – двум и последние два жмут руки друг другу.
7+6+5+4+3+2+1 = 28 рукопожатий.
Ответ: 28 рукопожатий.
Оценки:
ID_120 - 4+ б (хотели увидеть пояснения)
ID_113 - 113 - 4+ б
ID_102 - 0б
ID_132 - задача решена на 5 б, но решение было прислано не 5го, а 7 апреля (просим организаторов проекта рассмотреть вопрос о начислении балов)
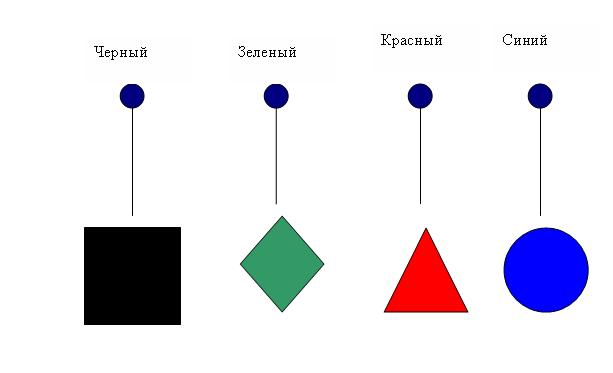
Задача 11. На столе лежат в ряд фигуры: треугольник, ромб, круг и квадрат. Цвета этих фигур - зеленый, чёрный, синий, красный. Фигура красного цвета лежит между зеленой и синей, справа от чёрной фигуры лежит ромб, круг лежит правее треугольника и ромба, причем треугольник лежит не с краю и, наконец, фигура синего цвета не лежит рядом с фигурой чёрного цвета. Какого цвета круг?
Решение:
Оценки:
ID_132 - задача решена на 3 б, но решение было прислано не 5, а 7 апреля (просим организаторов проекта рассмотреть вопрос о начислении балов )
Задача 12. Летом в городе N обувной магазин закрывается каждый понедельник, хозяйственный - каждый вторник, продовольственный каждый четверг, а парфюмерный магазин работает только по понедельникам, средам и пятницам. В воскресенье все магазины в городе закрыты. Однажды подруги Аня, Рита, Катя и Дина отправились за покупками, причем каждая в свой магазин. По дороге они обменялись такими замечаниями: Аня. Дина и я хотели пойти еще раньше на этой неделе, но не было такого дня, чтобы мы обе могли сделать наши покупки. Рита. Я не хотела идти сегодня, но завтра я уже не смогу купить то, что мне нужно. Катя. Я могла пойти и вчера и позавчера. Дина. А я могла бы пойти и вчера и завтра. Скажите, кому какой магазин нужен?
Решение:Подруги пошли в магазин в среду. Ане нужен был хозяйственный магазин, Рите – парфюмерный, Кате – продовольственный, Дине – обувной.
Примечание: Мы считаем, что для решения данной задачи рационально использовать таблицу. Таким же образом задачу решили участники команды ID_132.
Оценки:
ID_120 - 5б
ID_132 - задача решена на 4 б, но решение было прислано не 5, а 7 апреля (просим организаторов проекта рассмотреть вопрос о начислении балов )
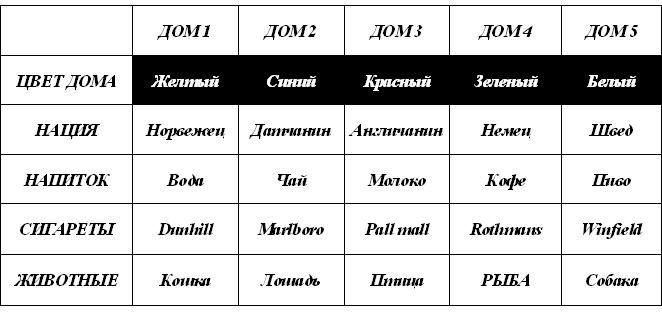
Задача 13. Есть 5 домов пяти pазличных цветов. В домах живут люди pазных национальностей. Эти пятеpо хозяев пьют pазные напитки, куpят pазличные виды сигаp и деpжат домшенее животное. Хозяева не имеют одинаковых животных, не куpят одинаковых сигаp и не пьют одних и тех же напитков.
Подсказки:
•Англичанин живет в красном доме
•Швед держит собаку
•Датчанин пьет чай
•Зеленый дом стоит слева от белого
•Жилец зеленого дома пьет кофе
•Человек, который курит Pallmall, держит птицу
•Жилец из среднего дома пьет молоко
•Жилец из желтого дома курит Dunhill
•Норвежец живет в первом доме
•Курильщик Marlboro живет около того, где держит кошку
•Человек, который содержит лошадь, живет около того, кто курит Dunhill
•Курильщик Winfield пьет пиво
•Норвежец живет около голубого дома
•Немец курит Rothmans
•Курильщик Marlboro живет по соседству с человеком, который пьет воду
Кто держит рыбу?
Решение:
1. Норвежец живет в первом доме
2. Норвежец живет около голубого дома (2-й)
3. Жилец из среднего дома пьет молоко (3-й)
4. Зеленый дом стоит слева от белого
5. Жилец зеленого дома пьет кофе
6. Зелёный дом – 4-й
7. Белый дом – 5-й
8. Англичанин живет в красном доме
9. Первый дом – желтый
10. Норвежец живет в желтом доме
11. Жилец из желтого дома курит Dunhill
12. Лошадь у жильца голубого дома
13. Датчанин пьет чай в голубом доме
14. Курильщик Winfield пьет пиво в белом доме
15. Норвежец пьёт воду
16. Курильщик Marlboro живет в голубом доме (датчанин)
17. Кошку держит Норвежец
18. Швед держит собаку в белом доме
19. Человек, который курит Pallmall, держит птицу – Англичанин
20. Значит, Немец курит Rothmans и держит рыбу
Таблица:
Ответ: Рыбу держит немец.
Оценки:
ID_132 - 0б
E-mail: poyarkova_olga@list.ru
Команда 123 "Введите название команды"
Команда 124 "Введите название команды"
Команда 125 "Введите название команды"
Команда 126 "Введите название команды"
Команда 127 "Пупс"
Задача №1
Окончилось соревнование, в котором каждая команда встретилась со всеми другими. Было проведено m встреч. Определите число команд, если m равно:
- 10
- 91
- 207
Задача №2 "Загадка бабы-Яги"
Прощаясь с Иваном -Царевичем, баба-Яга сказала:"От моей избушки отходят три пути, от каждого из них -еще три. Все пути ведут в Кощеево царство. Сколько их-считай сам, но самый коротким путь будет, если следовать моему совету: выбирай не самую первую дорогу, но левее правой!" По какому пути Иван-Царевич должен пойти в царство Кощея?
Задача №3 "Испытания Иванушки"
" Задаю тебе задачу,-сказала принцесса Иванушке,-принеси мне из сада розу, найдя самый верный путь из этой комнаты. В следующую комнату можно пройти через одну из дверей:левую, правую и центральную. Такие же три двери будут перед тобой при переходе из той, второй комнаты в третью, а из третьей-в сад."
"Учти мои советы,-продолжала принцесса.-Первый:из этого зала пройди через правую дверь. Второй: из второй комнаты через правую дверь не проходи. Третий: из третьей комнаты не проходи через левую дверь."
Иванушка знал, что обычно из трех советов принцессы двум следовать нельзя. Кроме того, служанка принцессы успела ему шепнуть, что надо обязательно пройти через дверь каждого вида по одному разу.
Как и полагается в сказке, принес Иванушка розу и был вознагражден. Какой же маршрут оказался единственно верным?
Задача №4 "Остров Ро-ко-ко"
На острове Ро-ко-ко живет племя, которое использует три буквы -"А", "Б", "В". В словах они могут повторяться не более двух раз каждая. Сколько различных слов у жителей этого острова, если все их слова трехбуквенные?
Задача №5
Экспозиция картинной галереи представляет собой систему коридоров, на обоих стенах которых развешаны картины:
Можно ли предложить такой маршрут осмотра экспозиции, при котором посетитель проходит вдоль каждой стены ровно один раз?
E-mail команды : doom_51_7@mail.ru
Команда 128 "Введите название команды"
Команда 129 "Введите название команды"
Команда 130 "Введите название команды"
Команда 131 "Введите название команды"
Команда 132 "ГРАФиК"
Задача №1
Докажите, что среди любых шести человек найдутся либо трое, друг с другом знакомые, либо трое, друг с другом незнакомые. Решение
Оценки:
ID_122 - 0 баллов
D_116 - 5 баллов
Задача №2
Купленные в подарок игрушки ( пистолет, сумочку, куклу, машину) уложили в четыре коробки, по одной игрушке в каждую. Требуется узнать, что положено в каждую коробку, если известно следующее: машинка и пистолет не в красной коробке; коробка с сумочкой находится между синей коробкой и коробкой с куклой; в зеленой коробке не сумочка и не машинка; желтая и зеленая коробки находятся около коробки с пистолетом.
Решение:
Пистолет- в синей, сумочка- в красной, кукла - в зелёной, машинка- в желтой
Оценки:
ID_113 - 5 баллов
ID_111 - 5 баллов
ID_122 - 5 баллов
ID_116 - 5 баллов
Задача №3
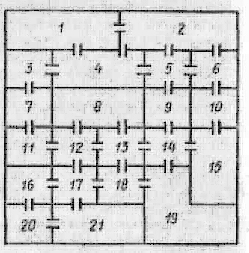
В походе, который длился 12 дней , участвовали 9 человек. Каждый день дежурили 3 человека. При этом дежурные ссорились друг с другом, и никакие двое из них не хотели больше ни разу дежурить вместе. Тем не менее участники похода утверждают, что все 12 дней им удавалось назначать тройки дежурных с учетом этого требования. Могло ли так быть?
РешениеУчастники похода обозначены цифрами от 1 до 9, каждая строчка соответствует тройке дежурных.
1 2 3
4 5 6
7 8 9
1 4 7
2 5 8
3 6 9
1 5 9
2 6 7
3 4 8
1 6 8
2 4 9
3 5 7
Или графом
Оценки:
ID_116 - 5 баллов
Задача №4
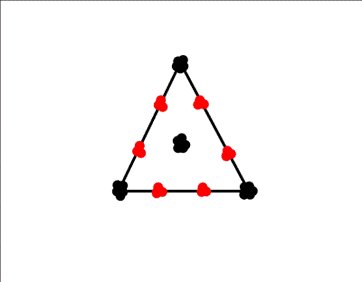
Садовнику поручили высадить 10 деревьев на площадке в форме равностороннего треугольника. Садовник имел два сорта деревьев: 10 акаций и 10 лип. Чтобы придать некоторое разнообразие саду, он решил посадить несколько акаций и несколько лип, причем так, чтобы на каждой стороне каждого из четырех равносторонних треугольников, которые при этом образовались , росло не больше двух деревьев того же сорта. Как он это сделал?
Решение:Садовник посадил 4 акации и 6 лип. Или графом
Оценки:
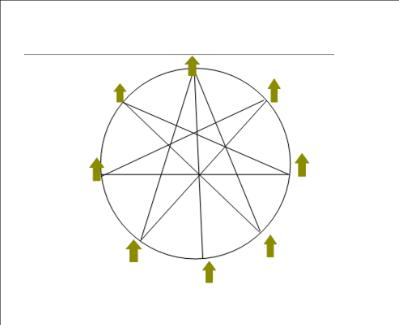
Задача №5
Царь Горох, побывавший однажды на острове Буяне, обратил внимание, что семь крепостей, защищающих остров, связаны прямолинейными дорогами, причем можно посетить все крепости , проезжая по каждой дороге ровно один раз. А самое удивительное – каждая из дорог пересекается со всеми остальными дорогами. Вернувшись домой, царь Горох повелел своему воеводе построить вокруг столицы восемь крепостей и точно так же связать их дорогами. Думал-думал воевода, но ничего не придумал. Попробуйте это сделать вы.
Решение:Одно из решений
Оценки:
Задача №6
В компании из N человек у каждого ровно трое друзей. Доказать, что N –четное число.
Решение:Подсчитаем число пар друзей. Поскольку каждый имеет трёх друзей, т. е. входит в три такие пары, то общее число пар равно 3N/2. Отсюда N-отсюда N-четное число. Или графом: люди- точки, друзей соединим отрезками- ребрами. У каждого из М ребер графа два конца и каждая из N вершин служит концом трёх ребер. 2М=3N, отсюда М=3N/2.
Оценки:
ID_122 - 3 балла( не учтено условие, что у каждого ровно трое друзей, поэтому в рассуждениях - у каждого из этих шести друзей еще по 2 друга (т.е. + 12) и т.д. допущена ошибка )
ID_116 - 5 балла
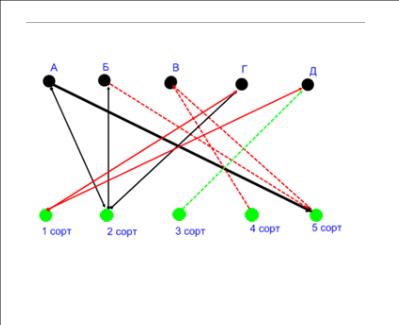
Задача №8
В пяти корзинах лежали яблоки пяти разных сортов. Яблоки первого сорта лежат в корзинах Г и Д; яблоки второго сорта- в корзинах А, Б, Г; в корзинах А, Б, В имеются яблоки пятого сорта, в корзине В имеются к тому же яблоки четвертого сорта, а в корзине Д- третьего. Пронумеруйте каждую корзину так, чтобы в корзине №1 были яблоки первого сорта (хотя бы одно); в корзине №2- второго и т. д.
Решение№1- Г; №2- А или №2- Б ; №3 - Д; №4 - В;№5 – Б или №5 – А.
Оценки:
ID_113 - 4балла( возможны 2 варианта)
ID_122 - 4балла( возможны 2 варианта)
ID_116 - 5 баллов
Задача №9
Какие буквы русского алфавита можно нарисовать одним росчерком?
Решение: Б, В, Г, З, И, Л, М, О, П, Р, С, Ф, Ъ, Ь, Я.
Оценки:
ID_113 - 4 балла(ъ)
ID_122 - 5 баллов
ID_116 - 5 баллов
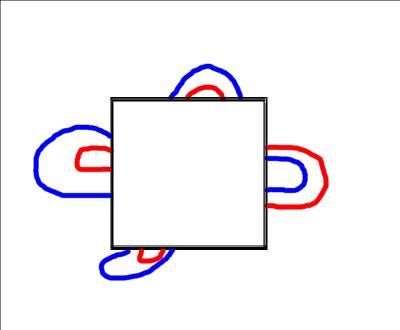
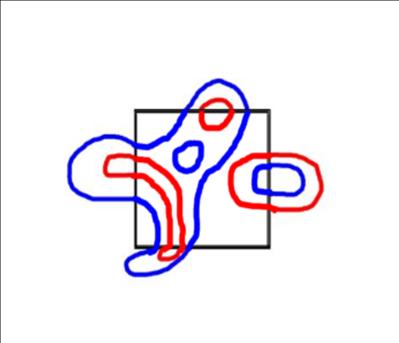
Задача №10
Мальчик нарисовал на бумаге три синих и три красных замкнутых контура, которые нигде не пересекались( рис). Затем рисунок накрыли листом бумаги так, что один из контуров оказался целиком накрыт, а все другие были частично видны. Нарисуйте закрытую часть рисунка.
Решение:
Оценки:
ID_113 - 0 баллов(Вы неучли следующее: рисунок накрыли листом бумаги так, что один из контуров оказался целиком накрыт, а все другие были частично видны.)
ID_122 - 0 баллов(Вы неучли следующее: рисунок накрыли листом бумаги так, что один из контуров оказался целиком накрыт, а все другие были частично видны.)
ID_116 - 0 баллов
E-mail команды: gulnara151173@yandex.ru