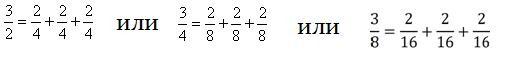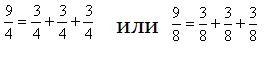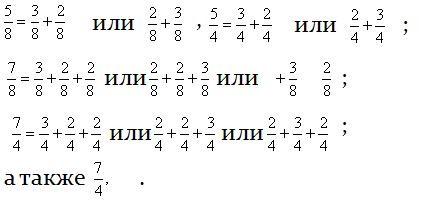Нужны ли дроби в музыке
(Новая: Слушание музыки: И.С. Бах. Ария из оркестровой сюиты.Мы услышим произведение композитора, который нам ...) |
|||
| (не показаны 37 промежуточных версий 2 участников) | |||
| Строка 1: | Строка 1: | ||
| − | + | '''Музыка и дроби''' | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | [[Изображение:Lmc.jpg|center|Описание]] | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | 1) В результате чего появились дроби? ( В результате деления. Дробь, дробить, делить). | |
| − | + | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | 2) Существует ли связь между математикой и музыкой, а в частности между обыкновенными дробями и музыкой? Ребята, которые учатся в музыкальной школе знают, как связаны ноты и дроби (рисунок 2). Чтобы найти длину такта, нужно сложить дроби (рисунок 1). | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | [[Изображение:And.jpg|left|Описание]] [[Изображение:Lcd.jpg|right|Описание|center]] | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | * Каждое настоящее искусство имеет свою теорию. Иногда эту теорию можно выразить в терминах математики. Музыка – это великое искусство, обладающее удивительной силой. | ||
| + | |||
| + | |||
| + | * На уроках математики мы изучали обыкновенные дроби и действия над дробями. В музыкальной школе на уроках теории музыки мы тоже изучаем дроби, но применительно к музыке. Поэтому я решила в своей работе показать связь в математике и музыке. | ||
| + | |||
| + | |||
| + | * Математики, начиная с Пифагора, постоянно проявляли интерес к музыке. В школе Пифагора получила свое первоначальное оформление математическая теория музыки. Об это напоминает математическая терминология, например «гармоническая пропорция». | ||
| + | |||
| + | |||
| + | * Говорят, что три числа образуют гармоническую пропорцию, если обратные им числа удовлетворяют непрерывной арифметической пропорции. | ||
| + | Оказывается длины трех струн, дающих ноты ДО, МИ, СОЛЬ, которые составляют один из наиболее благозвучных аккордов – мажорный, удовлетворяют гармонической пропорции, а числа колебаний этих струн образуют непрерывную арифметическую пропорцию. | ||
| + | |||
| + | |||
| + | * После создания точной математической теории струны, после того как физики и математики поняли, что любой музыкальный инструмент всего-навсего «физико-акустический прибор», - поле этого судьба музыки уже неотделима от математики. | ||
| + | |||
| + | |||
| + | В свое время английский математик Д.Сильвестр называл музыку – математикой чувств, а математику – музыкой разума. | ||
| + | |||
| + | |||
| + | |||
| + | Мы прослушали произведение композитора И.С. Баха Ария из оркестровой сюиты. Ответили на следующие вопросы: какие по длительности звуки использует композитор? | ||
| + | |||
| + | -Какова мелодия произведения?(''очень напевная, волнообразная''). | ||
| + | |||
| + | |||
| + | – Какие длительности преобладают в мелодии, почему? (''целые или половинные, потому что медленный темп и звуки долго тянутся''). | ||
| + | |||
| + | |||
| + | - Целая и половинная нота в музыке? Что получится, если перевести данные длительности на язык математики? Что на языке математики указывает на часть?(''целая нота – это целое число, половинная – это дробь''). | ||
| + | |||
| + | |||
| − | + | – Опера – это музыкально-сценический жанр, в котором главные герои выражают свои эмоции и чувства, главным образом, с помощью пения. | |
| − | + | ||
| − | + | ||
| − | + | - Как строится опера?(''увертюра – действия – финал''). | |
| − | + | ||
| − | + | ||
| − | + | - Именно опере посвящена наша следующая задача. | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
Композитор сочинял оперу 12 месяцев. Увертюру он сочинял 1/6 этого времени, 1 действие – 1/3 всего времени, 2 действие – 1/2 от затраченного времени на сочинение увертюры и 1 действия. Сколько времени композитор затратил на сочинение финала? | Композитор сочинял оперу 12 месяцев. Увертюру он сочинял 1/6 этого времени, 1 действие – 1/3 всего времени, 2 действие – 1/2 от затраченного времени на сочинение увертюры и 1 действия. Сколько времени композитор затратил на сочинение финала? | ||
| − | + | ||
| − | + | * '''Сложные 3-х частные такты состоят из : | |
| − | + | ||
| − | + | ''' | |
| − | + | а) 3-х простых 2-х частных тактов т.е. | |
| − | + | ||
| − | + | ||
| − | + | [[Изображение:Kaz.jpg|center|Описание]] | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | б) 3-х простых 3-х частных тактов т.е. | ||
| + | |||
| + | [[Изображение:Kpk.jpg|center|Описание]] | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | Смешанные такты - сложные такты, образованные из нескольких простых тактов различного размера: | ||
| + | |||
| + | |||
| + | [[Изображение:Lde.jpg|center|Описание]] | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | Определим еще одну музыкально-математическую связь. Математика - мудрая царица всех наук. Она сопровождает человека всю жизнь. И даже песни сочинялись о математике. | ||
| + | |||
Печальна и чиста, | Печальна и чиста, | ||
Как жизнь, людьми любима, | Как жизнь, людьми любима, | ||
Как жизнь, ты не проста, | Как жизнь, ты не проста, | ||
Как жизнь, непостижима, | Как жизнь, непостижима, | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | Работы наших одноклассников. | |
| + | |||
| + | [[Изображение:Kes.jpg|left|Описание]] [[Изображение:Led.jpg|right|Описание|center]] | ||
| + | |||
| + | [[Категория: ТГУ]] | ||
| + | |||
| + | [[Категория: TEO2]] | ||
Текущая версия на 22:40, 1 марта 2012
Музыка и дроби
1) В результате чего появились дроби? ( В результате деления. Дробь, дробить, делить).
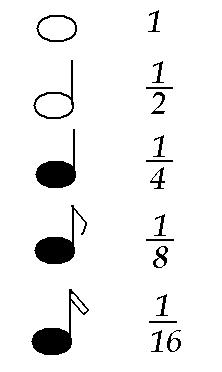
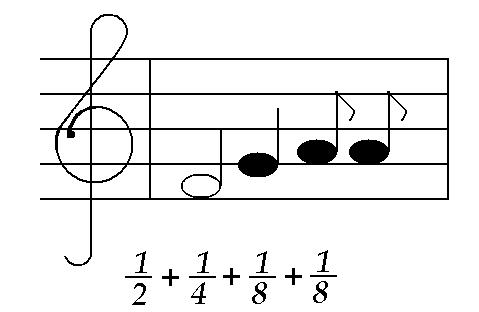
2) Существует ли связь между математикой и музыкой, а в частности между обыкновенными дробями и музыкой? Ребята, которые учатся в музыкальной школе знают, как связаны ноты и дроби (рисунок 2). Чтобы найти длину такта, нужно сложить дроби (рисунок 1).
- Каждое настоящее искусство имеет свою теорию. Иногда эту теорию можно выразить в терминах математики. Музыка – это великое искусство, обладающее удивительной силой.
- На уроках математики мы изучали обыкновенные дроби и действия над дробями. В музыкальной школе на уроках теории музыки мы тоже изучаем дроби, но применительно к музыке. Поэтому я решила в своей работе показать связь в математике и музыке.
- Математики, начиная с Пифагора, постоянно проявляли интерес к музыке. В школе Пифагора получила свое первоначальное оформление математическая теория музыки. Об это напоминает математическая терминология, например «гармоническая пропорция».
- Говорят, что три числа образуют гармоническую пропорцию, если обратные им числа удовлетворяют непрерывной арифметической пропорции.
Оказывается длины трех струн, дающих ноты ДО, МИ, СОЛЬ, которые составляют один из наиболее благозвучных аккордов – мажорный, удовлетворяют гармонической пропорции, а числа колебаний этих струн образуют непрерывную арифметическую пропорцию.
- После создания точной математической теории струны, после того как физики и математики поняли, что любой музыкальный инструмент всего-навсего «физико-акустический прибор», - поле этого судьба музыки уже неотделима от математики.
В свое время английский математик Д.Сильвестр называл музыку – математикой чувств, а математику – музыкой разума.
Мы прослушали произведение композитора И.С. Баха Ария из оркестровой сюиты. Ответили на следующие вопросы: какие по длительности звуки использует композитор?
-Какова мелодия произведения?(очень напевная, волнообразная).
– Какие длительности преобладают в мелодии, почему? (целые или половинные, потому что медленный темп и звуки долго тянутся).
- Целая и половинная нота в музыке? Что получится, если перевести данные длительности на язык математики? Что на языке математики указывает на часть?(целая нота – это целое число, половинная – это дробь).
– Опера – это музыкально-сценический жанр, в котором главные герои выражают свои эмоции и чувства, главным образом, с помощью пения.
- Как строится опера?(увертюра – действия – финал).
- Именно опере посвящена наша следующая задача.
Композитор сочинял оперу 12 месяцев. Увертюру он сочинял 1/6 этого времени, 1 действие – 1/3 всего времени, 2 действие – 1/2 от затраченного времени на сочинение увертюры и 1 действия. Сколько времени композитор затратил на сочинение финала?
- Сложные 3-х частные такты состоят из :
а) 3-х простых 2-х частных тактов т.е.
б) 3-х простых 3-х частных тактов т.е.
Смешанные такты - сложные такты, образованные из нескольких простых тактов различного размера:
Определим еще одну музыкально-математическую связь. Математика - мудрая царица всех наук. Она сопровождает человека всю жизнь. И даже песни сочинялись о математике.
Печальна и чиста,
Как жизнь, людьми любима,
Как жизнь, ты не проста,
Как жизнь, непостижима,
Работы наших одноклассников.