Семинар ДООМ Неравенство треугольника в примерах
| (не показаны 2 промежуточные версии 1 участника) | |||
| Строка 3: | Строка 3: | ||
[[Участник: Коннова Елена]] | [[Участник: Коннова Елена]] | ||
| − | Руководитель команд ДООМ 2009 [[Участник: | + | Руководитель команд ДООМ 2009 [[Участник:Многоугольник IDm083|Многоугольник IDm 083]] и [[Участник:Великие математики IDm082|Великие математики IDm 082]] |
| + | Место урока: факультатив, 7-8 класс | ||
| + | |||
| + | Вид урока: практикум по решению задач | ||
| + | |||
| + | [[Медиа:Неравенство_треугольника_082.ppt|Презентация к статье неравенство треугольника]] | ||
| + | |||
| + | Ход урока: | ||
| + | |||
| + | 1. Оргмомент | ||
| + | |||
| + | 2. Вступительное слово | ||
Неравенство треугольника в геометрии и смежных дисциплинах — это одно из интуитивных свойств расстояния. Оно утверждает, что длина любой стороны треугольника всегда не превосходит сумму длин двух его других сторон. Неравенство треугольника иногда включается как аксиома некоторой теории (например, оно включено в определение метрического пространства), иногда как теорема. | Неравенство треугольника в геометрии и смежных дисциплинах — это одно из интуитивных свойств расстояния. Оно утверждает, что длина любой стороны треугольника всегда не превосходит сумму длин двух его других сторон. Неравенство треугольника иногда включается как аксиома некоторой теории (например, оно включено в определение метрического пространства), иногда как теорема. | ||
| Строка 15: | Строка 26: | ||
равенство | AC | = | AB | + | BC | достигается только тогда, когда треугольник вырожден, и точка B лежит строго между A и C, на отрезке АС. | равенство | AC | = | AB | + | BC | достигается только тогда, когда треугольник вырожден, и точка B лежит строго между A и C, на отрезке АС. | ||
| − | + | [[Изображение:нертр1.JPG]] | |
Евклид в Началах доказывает неравенство треугольника следующим образом. Сначала доказывается теорема о том, что внешний угол треугольника больше внутреннего угла, с ним не смежного. Далее выводится теорема, что против большей стороны треугольника лежит больший внутренний угол. Затем методом от противного доказывается теорема о том, что против большего внутреннего угла треугольника лежит большая сторона. Из этой теоремы выводится неравенство треугольника. | Евклид в Началах доказывает неравенство треугольника следующим образом. Сначала доказывается теорема о том, что внешний угол треугольника больше внутреннего угла, с ним не смежного. Далее выводится теорема, что против большей стороны треугольника лежит больший внутренний угол. Затем методом от противного доказывается теорема о том, что против большего внутреннего угла треугольника лежит большая сторона. Из этой теоремы выводится неравенство треугольника. | ||
| Строка 27: | Строка 38: | ||
Каждый плоский угол трёхгранного угла меньше суммы двух других его плоских углов. | Каждый плоский угол трёхгранного угла меньше суммы двух других его плоских углов. | ||
| + | |||
| + | 3. Решение задач | ||
| + | |||
Задача 1: a, b, c – стороны треугольника. a = 3,17, b = 0,75, c – целое число. Найти c. | Задача 1: a, b, c – стороны треугольника. a = 3,17, b = 0,75, c – целое число. Найти c. | ||
| Строка 35: | Строка 49: | ||
Р0. Рассмотрим четырехугольник АВСD. Из неравенства треугольника BD<BC+CD, BC<BA+AD, тогда 2BD<BC+CD+DA+AB, 2BD<PABCD. | Р0. Рассмотрим четырехугольник АВСD. Из неравенства треугольника BD<BC+CD, BC<BA+AD, тогда 2BD<BC+CD+DA+AB, 2BD<PABCD. | ||
| − | + | [[Изображение:нертр2.JPG]] | |
Задача 3: Доказать, что в четырехугольнике любая сторона меньше суммы остальных. | Задача 3: Доказать, что в четырехугольнике любая сторона меньше суммы остальных. | ||
| Строка 47: | Строка 61: | ||
РЕШЕНИЕ. Рассмотрим четырехугольник АВСD. Продлим отрезок МР до пересечения со сторонами четырехугольника – К и Т. | РЕШЕНИЕ. Рассмотрим четырехугольник АВСD. Продлим отрезок МР до пересечения со сторонами четырехугольника – К и Т. | ||
| − | + | [[Изображение:нертр3.JPG]] | |
КТ>РМ. Т.к. в четырехугольнике любая сторона меньше суммы остальных (задача 3), то КТ<КD+DC+CT, KT<KA+AB+BT, получаем 2KT<PABCD и РМ < KT < 0.5PABCD. | КТ>РМ. Т.к. в четырехугольнике любая сторона меньше суммы остальных (задача 3), то КТ<КD+DC+CT, KT<KA+AB+BT, получаем 2KT<PABCD и РМ < KT < 0.5PABCD. | ||
| Строка 63: | Строка 77: | ||
Решение. | Решение. | ||
| − | + | [[Изображение:нертр4.JPG]] | |
На продолжении стороны AB за точку A отложим отрезок AF , равный AB . Треугольник ADF равен треугольнику CEB по двум сторонам и углу между ними. Значит, DF = BE . Применив неравенство треугольника к треугольнику FDB , получим, что | На продолжении стороны AB за точку A отложим отрезок AF , равный AB . Треугольник ADF равен треугольнику CEB по двум сторонам и углу между ними. Значит, DF = BE . Применив неравенство треугольника к треугольнику FDB , получим, что | ||
Текущая версия на 22:12, 6 декабря 2009
Неравенство треугольника в примерах
Руководитель команд ДООМ 2009 Многоугольник IDm 083 и Великие математики IDm 082
Место урока: факультатив, 7-8 класс
Вид урока: практикум по решению задач
Презентация к статье неравенство треугольника
Ход урока:
1. Оргмомент
2. Вступительное слово
Неравенство треугольника в геометрии и смежных дисциплинах — это одно из интуитивных свойств расстояния. Оно утверждает, что длина любой стороны треугольника всегда не превосходит сумму длин двух его других сторон. Неравенство треугольника иногда включается как аксиома некоторой теории (например, оно включено в определение метрического пространства), иногда как теорема.
Евклидова геометрия
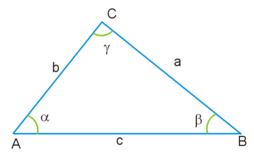
Длина любой стороны треугольника не превосходит сумму длин двух других.
Пусть дан треугольник ΔABC. Тогда | AC | ≤ | AB | + | BC |, причём равенство | AC | = | AB | + | BC | достигается только тогда, когда треугольник вырожден, и точка B лежит строго между A и C, на отрезке АС.
Евклид в Началах доказывает неравенство треугольника следующим образом. Сначала доказывается теорема о том, что внешний угол треугольника больше внутреннего угла, с ним не смежного. Далее выводится теорема, что против большей стороны треугольника лежит больший внутренний угол. Затем методом от противного доказывается теорема о том, что против большего внутреннего угла треугольника лежит большая сторона. Из этой теоремы выводится неравенство треугольника.
Обратное неравенство треугольника
Следствием неравенства треугольника является неравенство: | AC | - | AB | ≥ | BC |
Неравенство треугольника для трехгранного угла
Каждый плоский угол трёхгранного угла меньше суммы двух других его плоских углов.
3. Решение задач
Задача 1: a, b, c – стороны треугольника. a = 3,17, b = 0,75, c – целое число. Найти c.
РЕШЕНИЕ. Из неравенства треугольника c < a+b, с<3,17+0,75, с< 3,92; но из обратного неравенства треугольника c>a-b, т.е. с> 3,17-0,75, c>2,42. Т.к. с - целое число, оно равно 3.
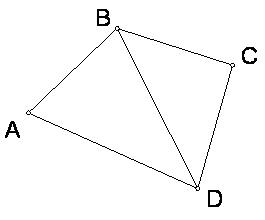
Задача 2: Доказать, что в четырехугольнике диагональ меньше половины периметра.
Р0. Рассмотрим четырехугольник АВСD. Из неравенства треугольника BD<BC+CD, BC<BA+AD, тогда 2BD<BC+CD+DA+AB, 2BD<PABCD.
Задача 3: Доказать, что в четырехугольнике любая сторона меньше суммы остальных.
РЕШЕНИЕ. Рассмотрим четырехугольник АВСD. Из неравенства треугольника AB<AD+DB, BD<BC+CD, отсюда AB<AD+BC+CD.
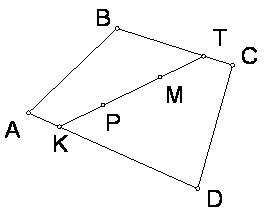
Задача 4: М и Р – точки внутри многоугольника. Доказать, что расстояние между ними меньше половины периметра многоугольника.
РЕШЕНИЕ. Рассмотрим четырехугольник АВСD. Продлим отрезок МР до пересечения со сторонами четырехугольника – К и Т.
КТ>РМ. Т.к. в четырехугольнике любая сторона меньше суммы остальных (задача 3), то КТ<КD+DC+CT, KT<KA+AB+BT, получаем 2KT<PABCD и РМ < KT < 0.5PABCD.
Аналогично доказывается для случая, когда прямая АВ пересекает соседние стороны четырехугольника или проходит через вершину.
Задача 5: Есть 7 реек длиннее 9 см, но короче 1 м. Доказать, что из трех из них можно составить треугольник.
РЕШЕНИЕ. Предположим, что треугольник составить нельзя. Берем 2 самых коротких, их длина больше 9 см. Следующим должен быть больше 9 + 9 = 18 см, иначе можно составить треугольник. Четвертый больше 18 + 9 = 27, пятый больше 27 + 18 = 45, шестой больше 45 + 27 = 72, и последний будет больше 72 + 45 = 112, что больше метра. Получили противоречие. Значит, из трех из них можно составить треугольник.
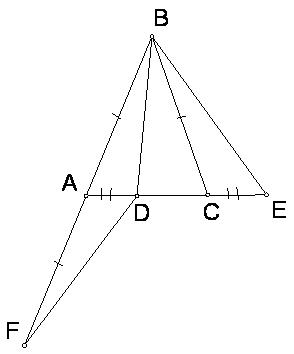
Задача 6. На основании AC равнобедренного треугольника ABC выбрали точку D, а на продолжении AC за вершину C – точку E , причём AD=CE . Докажите, что BD+BE > AB+BC .
Решение.
На продолжении стороны AB за точку A отложим отрезок AF , равный AB . Треугольник ADF равен треугольнику CEB по двум сторонам и углу между ними. Значит, DF = BE . Применив неравенство треугольника к треугольнику FDB , получим, что AB+BC = BF < BD+DF = BD + BE, что и требовалось доказать.
Литература: Словари и энциклопедии на Академике [1]
wiki.iteach.ru/images/4/4a/БаженовЗадачи.doc
Задача по геометрии из коллекции задач Р.К. Гордина [2].