Семинар ДООМ. Решение комбинаторных задач с помощью графов
| (не показаны 25 промежуточных версий 1 участника) | |||
| Строка 1: | Строка 1: | ||
[[Участник:Янина Ирина Владимировна]] | [[Участник:Янина Ирина Владимировна]] | ||
| + | |||
[[Участник:ЛОГО 053]] | [[Участник:ЛОГО 053]] | ||
| Строка 6: | Строка 7: | ||
Для внеклассной работы комбинаторные задачи привлекательны тем, что легко могут быть оформлены в виде головоломок. Они неизменно вызывают у учащихся большой интерес. А так как способы их решения резко отличаются от обычных школьных, знакомство с ними способствует развитию математического мышления школьников. | Для внеклассной работы комбинаторные задачи привлекательны тем, что легко могут быть оформлены в виде головоломок. Они неизменно вызывают у учащихся большой интерес. А так как способы их решения резко отличаются от обычных школьных, знакомство с ними способствует развитию математического мышления школьников. | ||
| + | |||
Возраст учащихся требует пока не включать в содержание комбинаторные формулы. | Возраст учащихся требует пока не включать в содержание комбинаторные формулы. | ||
Все задачи на занятии разбиты на блоки, связанные единой идеей решения. Внутри блока задачи располагаются по возрастанию степени сложности. | Все задачи на занятии разбиты на блоки, связанные единой идеей решения. Внутри блока задачи располагаются по возрастанию степени сложности. | ||
| − | ''' | + | <h2>'''Цели'''</h2> |
| + | |||
| + | '''•''' знакомство с новым способом решения комбинаторных задач; | ||
| + | |||
| + | '''•''' развитие математического мышления и логики; | ||
| + | |||
| + | '''•''' повышение интереса к изучению математики. | ||
| + | |||
| + | |||
| + | <h2>'''Ход занятия.'''</h2> | ||
| + | |||
| + | <h3>'''''Первое знакомство с графом.'''''</h3> | ||
| + | |||
| + | На прошлом занятии учащиеся научились составлять соединения из небольшого числа предметов. Поэтому они легко могут решить непосредственным перебором вариантов задачу: | ||
| + | |||
| + | '''Задача.''' У Лёвы 2 конверта: обычный и авиа, и 3 марки: прямоугольная, квадратная и треугольная. Сколькими способами он может выбрать конверт и марку, чтобы отправить письмо? | ||
| + | Учащиеся легко убеждаются, что всего вариантов 6. | ||
| + | |||
| + | Учитель предлагает удобный способ решения таких задач, при котором трудно пропустить какую-нибудь возможность – построение графа: фигуры, состоящей из точек (вершин графа) и отрезков, которые их соединяют (рёбер графа). | ||
| + | |||
| + | |||
| + | [[Изображение: logo1.GIF]] | ||
| + | |||
| + | |||
| + | Граф для данной задачи строится в два этапа: сначала мы выбираем конверт, а потом марку. | ||
| + | |||
| + | <center>[[Изображение:logo2.GIF]]</center> | ||
| + | |||
| + | |||
| + | |||
| + | <h3>''''' Решение задач первого блока с помощью графов.'''''</h3> | ||
| + | |||
| + | Эти задачи ярко демонстрируют преимущества решения задач с помощью графа перед непосредственным перебором вариантов: | ||
| + | |||
| + | '''Задача 1.1''' Ужасные грабители Кнопка и Скрепка решили украсть из сейфа золотой ключик Буратино. Для того чтобы открыть замок входной двери, им нужно подобрать двузначный код. Причём известно, что дверь запирает Буратино, который знает пока ещё только 4 цифры: 1, 2, 3, 4. Сколько вариантов придётся перебрать Кнопке и Скрипке, чтобы проникнуть в дом? | ||
| + | |||
| + | |||
| + | [[Изображение:logo3.GIF]] | ||
| + | |||
| + | |||
| + | '''Задача 1.2''' Проникнуть в дом – полдела. Кнопке и Скрепке нужно ещё открыть сейф. Но сейф запирает папа Карло, а он знает все цифры. Сколько двузначных кодов нужно перебрать грабителям, чтобы открыть сейф? | ||
| + | |||
| + | |||
| + | '''Задача 1.3''' У ковбоя Джека две лошади: каурой и гнедой масти, два седла: красное и зелёное, две пары шпор: длинные и короткие, два револьвера: один марки «Кольт», другой – «Смит – и – Вессон». Сколькими способами Джек может экипироваться для конной прогулки по прериям? | ||
| + | |||
| + | [[Изображение:logo4.GIF]] | ||
| + | |||
| + | '''Задача 1.4''' Космический корабль «Циклоп» опустился на неизвестную планету Х звезды V созвездия Центавр. Планета оказалась обитаема и разделена океанами на три материка. Каждый материк выдвинул трёх представителей для того, чтобы лететь с кораблём на Землю. Представителей первого материка зовут Ман, Зан, Сан, второго – Пын, Фын, Шин, третьего – Хыр, Кыр, Дыр. Но на «Циклопе» не хватит анабиозных ванн для девяти человек. Он может взять только трёх. Сколько способов у инопланетян составить делегацию на Землю? | ||
| + | |||
| + | [[Изображение:logo5.GIF]] | ||
| + | |||
| + | Учащиеся легко найдут ответ и, не вычерчивая граф полностью. | ||
| + | |||
| + | |||
| + | <h3>'''''Решение задач второго блока способом умножения.'''''</h3> | ||
| + | Задачи первого блока позволят естественно перейти к решению задач второго блока способом умножения. | ||
| + | |||
| + | |||
| + | '''Задача 2.1''' У Кролика две табуретки: красная и зелёная. К нему в гости пришли Винни-Пух и Пятачок. Сколькими способами он может рассадить гостей? | ||
| + | |||
| + | Решение. | ||
| + | На красную табуретку может сесть или Пятачок, или Пух. В любом случае на оставшуюся табуретку сядет второй гость, т. е. всего два способа. | ||
| + | |||
| + | |||
| + | '''Задача 2.2''' В следующий раз к Кролику пришли три гостя: Вини-Пух, Пятачок и ослик Иа. Сколькими способами он может рассадить гостей на синей, красной и жёлтой табуретках? | ||
| + | |||
| + | Решение. | ||
| + | Сначала учащиеся решают задачу перебором. Затем учитель предлагает провести такие же рассуждения, как и в предыдущей задаче: на красную табуретку может сесть или Пух, или Пятачок, или Иа. Всего имеются 3 возможности. На синюю табуретку сядет один из двух оставшихся гостей. Ну а на жёлтую табуретку сядет тот, гость, который не успел занять ни красную, ни синюю. Получается 3×2×1=6 способов. | ||
| + | |||
| + | |||
| + | '''Задача 2.3''' Сколькими способами Кролик может рассадить пять гостей на пяти разных табуретках? | ||
| + | |||
| + | Решение. | ||
| + | Рассуждая аналогично предыдущей задаче, ребята получают ответ 5×4×3×2×1=120 способов. | ||
| + | Учитель подводит итог: двух гостей на две табуретки можно рассадить 2×1=2 способами; трёх гостей на три табуретки можно рассадить 3×2×1=6 способами; четырёх гостей на четыре табуретки - 4×3×2×1=24 способами; пять гостей на пять табуреток - 5×4×3×2×1=120 способами. | ||
| + | Здесь уместно сообщить, что произведения 1×2×3×4×5 обозначается 5!, ввести термин «факториал» и предложить учащимся вычислить 6! и 7!. | ||
| + | |||
| + | |||
| + | После решения задач второго блока можно вернуться к первому блоку задач и решить их способом умножения. | ||
| + | |||
| + | |||
| + | <h3>'''''Решение задач третьего блока.'''''</h3> | ||
| + | |||
| + | Учащиеся упражняются в решении задач способом умножения. | ||
| + | |||
| + | |||
| + | '''Задача 3.1''' На борту космического корабля «Циклоп» три пилота и два инженера. | ||
| + | Сколькими способами можно составить экипаж разведывательного катера из одного пилота и одного инженера. | ||
| + | |||
| + | Ответ: шестью способами. | ||
| + | |||
| + | |||
| + | '''Задача 3.2''' В некотором городе у всех велосипедистов были трёхзначные номера. Но велосипедисты попросили, чтобы в этих номерах не встречались цифры 0 и 8, потому что первая из них похожа на вытянутое колесо, ну а что для велосипедиста «восьмёрка» колеса – знает каждый. Хватит ли им номеров, если в этом городе велосипеды имеют 710 человек? | ||
| + | |||
| + | Решение. | ||
| + | Для выбора цифры сотен номера имеется восемь возможностей, а именно 1,2,3,4,5,6,7,9. Столько же возможностей для выбора цифры десятков и единиц. Всего номеров будет 8×8×8=512. Так что для всех обладателей велосипедов их не хватит. | ||
| + | |||
| + | |||
| + | '''Задача 3.3''' Хватит ли номеров, если велосипедисты смягчат свои требования и согласятся на цифру 0? | ||
| + | |||
| + | Ответ: конечно, хватит. Номеров будет 9×9×9=729. | ||
| + | |||
| + | |||
| + | '''Задача 3.4''' В пятом классе изучаются восемь предметов. В среду пять уроков, и все они различны. Сколькими способами можно составить расписание на среду? | ||
| + | |||
| + | Ответ: всего 8×7×6×5×4=6720 способов. | ||
| + | |||
| + | |||
| + | <h3>''''' Решение задач четвёртого блока помощью графов.'''''</h3> | ||
| + | |||
| + | Получив в руки такое мощное оружие, как граф, учащиеся смогут решать задачи, в условии которых на соединения наложены какие-либо ограничения (в этом случае использовать способ умножения значительно сложнее). | ||
| + | |||
| + | |||
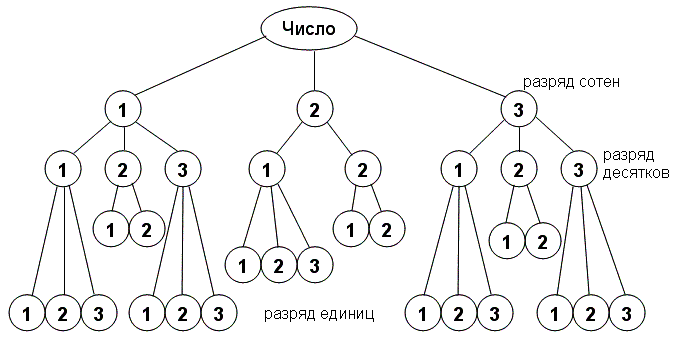
| + | '''Задача 4.1''' Сколько существует трёхзначных чисел, состоящих только из цифр 1, 2, 3, причём после двойки не стоит три? | ||
| + | |||
| + | [[Изображение:logo6.GIF]] | ||
| + | |||
| + | |||
| + | '''Задача 4.2''' По условию матча между шахматистами А и В победителем считается тот, кто первый выиграет у противника три партии (не обязательно подряд). Ничьи исключаются. Сколькими способами может сложиться ход матча? | ||
| + | |||
| + | <center>[[Изображение:logo7.GIF]]</center> | ||
| + | |||
| + | Решение. | ||
| + | При построении графа будем выписывать обозначение того шахматиста, который выигрывает партию. Партию. На которой игра заканчивается, обводим кружком. | ||
| + | Всего получается 20 вариантов исхода матча: два состоят из двух партий, шесть – из четырёх, двенадцать – из пяти. | ||
| + | |||
| + | |||
| + | '''Задача 4.3''' Команда космического корабля «Поиск» должна состоять из командира, пилота и врача. Возможны три кандидата на пост командира, назовём их а1, а2. a3, три на пост пилота –b1, b2, b3 и два на пост врача – с1, с2. При изучении вопроса о психологической совместимости членов экипажа выяснилось, что: | ||
| + | |||
| + | - а1 несовместим c b2 и с1; | ||
| + | |||
| + | - а2 несовместим с b3; | ||
| + | |||
| + | - а3 несовместим с b3 и с2; | ||
| + | |||
| + | - b2 несовместим с с2; | ||
| + | |||
| + | - b3 несовместим с с1. | ||
| + | |||
| + | Сколько вариантов экипажей возможно? | ||
| + | |||
| + | [[Изображение:logo8.GIF]] | ||
| + | |||
| + | |||
| + | <h2>'''''Итог занятия.'''''</h2> | ||
| + | |||
| + | Мы сегодня на занятии: | ||
| + | |||
| + | - познакомились с новым способом решения комбинаторных задач; | ||
| + | |||
| + | - убедились в том, что использование графа делает решение задачи более наглядным; | ||
| + | |||
| + | - рассмотренные задачи ярко демонстрируют преимущества такой схемы перед непосредственным перебором вариантов. | ||
| + | |||
| + | В дальнейшем мы продолжим знакомство с графами и их применениями. | ||
| + | Тема следующего занятия «Фигуры, рисуемые одним росчерком». | ||
| + | |||
| + | [[Категория:Проект ДООМ 2007-2008 (1 цикл)]] | ||
Текущая версия на 15:05, 10 января 2008
Участник:Янина Ирина Владимировна
Содержание |
Занятие математического кружка в 5 классе
Для внеклассной работы комбинаторные задачи привлекательны тем, что легко могут быть оформлены в виде головоломок. Они неизменно вызывают у учащихся большой интерес. А так как способы их решения резко отличаются от обычных школьных, знакомство с ними способствует развитию математического мышления школьников.
Возраст учащихся требует пока не включать в содержание комбинаторные формулы. Все задачи на занятии разбиты на блоки, связанные единой идеей решения. Внутри блока задачи располагаются по возрастанию степени сложности.
Цели
• знакомство с новым способом решения комбинаторных задач;
• развитие математического мышления и логики;
• повышение интереса к изучению математики.
Ход занятия.
Первое знакомство с графом.
На прошлом занятии учащиеся научились составлять соединения из небольшого числа предметов. Поэтому они легко могут решить непосредственным перебором вариантов задачу:
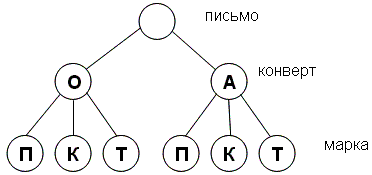
Задача. У Лёвы 2 конверта: обычный и авиа, и 3 марки: прямоугольная, квадратная и треугольная. Сколькими способами он может выбрать конверт и марку, чтобы отправить письмо? Учащиеся легко убеждаются, что всего вариантов 6.
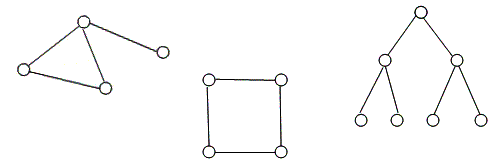
Учитель предлагает удобный способ решения таких задач, при котором трудно пропустить какую-нибудь возможность – построение графа: фигуры, состоящей из точек (вершин графа) и отрезков, которые их соединяют (рёбер графа).
Граф для данной задачи строится в два этапа: сначала мы выбираем конверт, а потом марку.
Решение задач первого блока с помощью графов.
Эти задачи ярко демонстрируют преимущества решения задач с помощью графа перед непосредственным перебором вариантов:
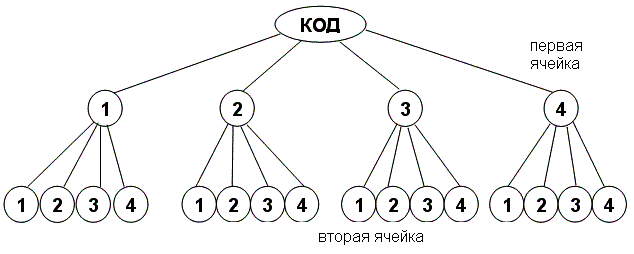
Задача 1.1 Ужасные грабители Кнопка и Скрепка решили украсть из сейфа золотой ключик Буратино. Для того чтобы открыть замок входной двери, им нужно подобрать двузначный код. Причём известно, что дверь запирает Буратино, который знает пока ещё только 4 цифры: 1, 2, 3, 4. Сколько вариантов придётся перебрать Кнопке и Скрипке, чтобы проникнуть в дом?
Задача 1.2 Проникнуть в дом – полдела. Кнопке и Скрепке нужно ещё открыть сейф. Но сейф запирает папа Карло, а он знает все цифры. Сколько двузначных кодов нужно перебрать грабителям, чтобы открыть сейф?
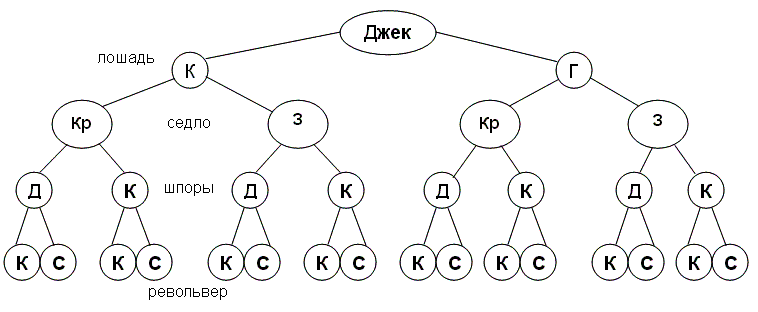
Задача 1.3 У ковбоя Джека две лошади: каурой и гнедой масти, два седла: красное и зелёное, две пары шпор: длинные и короткие, два револьвера: один марки «Кольт», другой – «Смит – и – Вессон». Сколькими способами Джек может экипироваться для конной прогулки по прериям?
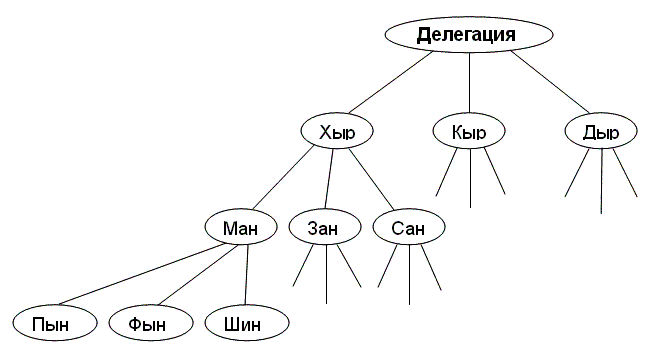
Задача 1.4 Космический корабль «Циклоп» опустился на неизвестную планету Х звезды V созвездия Центавр. Планета оказалась обитаема и разделена океанами на три материка. Каждый материк выдвинул трёх представителей для того, чтобы лететь с кораблём на Землю. Представителей первого материка зовут Ман, Зан, Сан, второго – Пын, Фын, Шин, третьего – Хыр, Кыр, Дыр. Но на «Циклопе» не хватит анабиозных ванн для девяти человек. Он может взять только трёх. Сколько способов у инопланетян составить делегацию на Землю?
Учащиеся легко найдут ответ и, не вычерчивая граф полностью.
Решение задач второго блока способом умножения.
Задачи первого блока позволят естественно перейти к решению задач второго блока способом умножения.
Задача 2.1 У Кролика две табуретки: красная и зелёная. К нему в гости пришли Винни-Пух и Пятачок. Сколькими способами он может рассадить гостей?
Решение. На красную табуретку может сесть или Пятачок, или Пух. В любом случае на оставшуюся табуретку сядет второй гость, т. е. всего два способа.
Задача 2.2 В следующий раз к Кролику пришли три гостя: Вини-Пух, Пятачок и ослик Иа. Сколькими способами он может рассадить гостей на синей, красной и жёлтой табуретках?
Решение. Сначала учащиеся решают задачу перебором. Затем учитель предлагает провести такие же рассуждения, как и в предыдущей задаче: на красную табуретку может сесть или Пух, или Пятачок, или Иа. Всего имеются 3 возможности. На синюю табуретку сядет один из двух оставшихся гостей. Ну а на жёлтую табуретку сядет тот, гость, который не успел занять ни красную, ни синюю. Получается 3×2×1=6 способов.
Задача 2.3 Сколькими способами Кролик может рассадить пять гостей на пяти разных табуретках?
Решение. Рассуждая аналогично предыдущей задаче, ребята получают ответ 5×4×3×2×1=120 способов. Учитель подводит итог: двух гостей на две табуретки можно рассадить 2×1=2 способами; трёх гостей на три табуретки можно рассадить 3×2×1=6 способами; четырёх гостей на четыре табуретки - 4×3×2×1=24 способами; пять гостей на пять табуреток - 5×4×3×2×1=120 способами. Здесь уместно сообщить, что произведения 1×2×3×4×5 обозначается 5!, ввести термин «факториал» и предложить учащимся вычислить 6! и 7!.
После решения задач второго блока можно вернуться к первому блоку задач и решить их способом умножения.
Решение задач третьего блока.
Учащиеся упражняются в решении задач способом умножения.
Задача 3.1 На борту космического корабля «Циклоп» три пилота и два инженера.
Сколькими способами можно составить экипаж разведывательного катера из одного пилота и одного инженера.
Ответ: шестью способами.
Задача 3.2 В некотором городе у всех велосипедистов были трёхзначные номера. Но велосипедисты попросили, чтобы в этих номерах не встречались цифры 0 и 8, потому что первая из них похожа на вытянутое колесо, ну а что для велосипедиста «восьмёрка» колеса – знает каждый. Хватит ли им номеров, если в этом городе велосипеды имеют 710 человек?
Решение. Для выбора цифры сотен номера имеется восемь возможностей, а именно 1,2,3,4,5,6,7,9. Столько же возможностей для выбора цифры десятков и единиц. Всего номеров будет 8×8×8=512. Так что для всех обладателей велосипедов их не хватит.
Задача 3.3 Хватит ли номеров, если велосипедисты смягчат свои требования и согласятся на цифру 0?
Ответ: конечно, хватит. Номеров будет 9×9×9=729.
Задача 3.4 В пятом классе изучаются восемь предметов. В среду пять уроков, и все они различны. Сколькими способами можно составить расписание на среду?
Ответ: всего 8×7×6×5×4=6720 способов.
Решение задач четвёртого блока помощью графов.
Получив в руки такое мощное оружие, как граф, учащиеся смогут решать задачи, в условии которых на соединения наложены какие-либо ограничения (в этом случае использовать способ умножения значительно сложнее).
Задача 4.1 Сколько существует трёхзначных чисел, состоящих только из цифр 1, 2, 3, причём после двойки не стоит три?
Задача 4.2 По условию матча между шахматистами А и В победителем считается тот, кто первый выиграет у противника три партии (не обязательно подряд). Ничьи исключаются. Сколькими способами может сложиться ход матча?
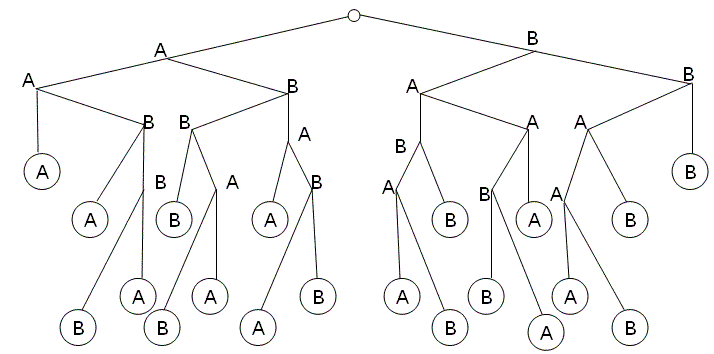
Решение. При построении графа будем выписывать обозначение того шахматиста, который выигрывает партию. Партию. На которой игра заканчивается, обводим кружком. Всего получается 20 вариантов исхода матча: два состоят из двух партий, шесть – из четырёх, двенадцать – из пяти.
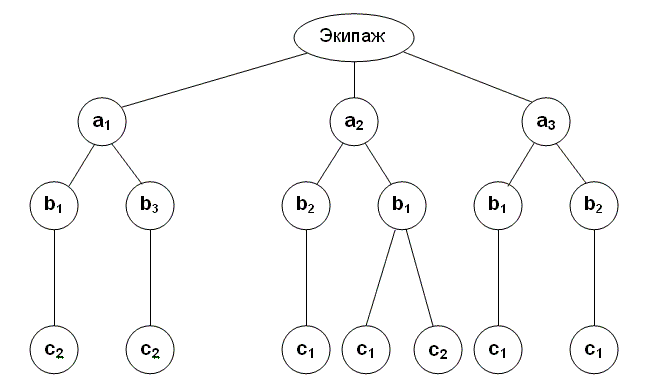
Задача 4.3 Команда космического корабля «Поиск» должна состоять из командира, пилота и врача. Возможны три кандидата на пост командира, назовём их а1, а2. a3, три на пост пилота –b1, b2, b3 и два на пост врача – с1, с2. При изучении вопроса о психологической совместимости членов экипажа выяснилось, что:
- а1 несовместим c b2 и с1;
- а2 несовместим с b3;
- а3 несовместим с b3 и с2;
- b2 несовместим с с2;
- b3 несовместим с с1.
Сколько вариантов экипажей возможно?
Итог занятия.
Мы сегодня на занятии:
- познакомились с новым способом решения комбинаторных задач;
- убедились в том, что использование графа делает решение задачи более наглядным;
- рассмотренные задачи ярко демонстрируют преимущества такой схемы перед непосредственным перебором вариантов.
В дальнейшем мы продолжим знакомство с графами и их применениями. Тема следующего занятия «Фигуры, рисуемые одним росчерком».