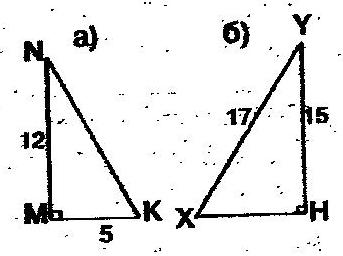Семинар ДООМ:«Решение задач на применение теоремы Пифагора»

Версия 18:05, 14 декабря 2009

Дегтева Людмила Викторовна id_002 О!

Урок по теме:

«Решение задач на применение теоремы Пифагора»

Тип урока: обобщение и систематизация знаний.

Цели урока:

• закрепление теоремы Пифагора и теоремы, обратной теореме Пифагора;

• совершенствование навыков решения задач на применение теоремы Пифагора и теоремы, обратной теореме Пифагора;

• развитие умений выявлять закономерности;

• повышение интереса к предмету.

Фронтальный опрос: теорема Пифагора, теорема ей обратная.

Решение задач по готовому чертежу.

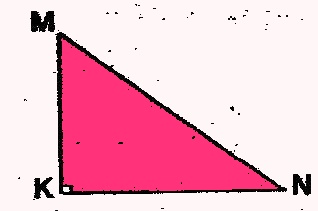
1. Записать теорему Пифагора для данного треугольника:

2. Найти неизвестную сторону треугольника:

3. ABCD–параллелограмм.Найти: СD.

4. Выясните, является ли треугольник прямоугольным, если его стороны выражаются числами: а) 6,8,10; б) 5,6,7; в) 9,12,15; г) 15,20,25. В каждом случае ответ обоснуйте.

Работа в парах.

1 уровень:

1. Диагонали ромба равны 14 и 48 см. Найдите сторону ромба.

2. В треугольнике два угла равны 450 и 900, а большая сторона 20см. найдите две другие стороны треугольника.

2 уровень:

1. В прямоугольной трапеции основания равны 5 и 17 см, а большая боковая сторона 13 см. Найдите площадь трапеции.

2. В треугольнике две стороны равны 10 и 12 см, а угол между ними 450. Найдите площадь треугольника.

Совместная проверка по слайдам. Подведение итогов работы.

Итоговый контроль

Задача 1. (2 балла)

Боковая сторона равнобедренного треугольника равна 10см, а высота, проведенная к основанию, равна 6 см. Найти площадь треугольника.

Задача 2. (3 балла)

Сторона ромба равна 13см, а одна из диагоналей 10см. Найти вторую диагональ ромба.

Задача 3. (4 балла)

Катет прямоугольного треугольника равен 8, гипотенуза 10. Найти высоту, проведенную к гипотенузе.

Ответы:48; 24; 4,8.

Критерии оценки:

2-3 балла—«3»

4-5 баллов—«4»

6 и более – «5»

Подведение итогов урока.