"Поиск кратчайшего пути"
Triada63 (обсуждение | вклад) (→Раскрытие вопроса) |
Triada63 (обсуждение | вклад) (→Раскрытие вопроса) |
||
| Строка 24: | Строка 24: | ||
Алгоритм Форда-Беллмана позволяет решить задачу о кратчайшем пути из фиксированного истока в общем случае, когда вес любого ребра может быть отрицательным. Этот алгоритм отличается своей простотой. К его достоинствам также относится то, что он определяет, содержится ли в графе цикл с отрицательным весом, достижимый из истока. Алгоритм Дейкстры характеризуется меньшим временем выполнения, чем алгоритм Форда-Беллмана, и менее претезателен чем другие алгоритмы. Кроме того, приведен алгоритм динамического программирования — алгоритм Флойда-Уоршалла (Floyd-Warshall), который позволяет решить задачу о поиске кратчайших путей между всеми парами вершин, он очень прост в освоении и с него начинают изучение темы алгоритмов поиска кратчайшего пути, но у него очень низкая скорость работы и в нем не предусмотрен просчет ребер с отрицательным весом. | Алгоритм Форда-Беллмана позволяет решить задачу о кратчайшем пути из фиксированного истока в общем случае, когда вес любого ребра может быть отрицательным. Этот алгоритм отличается своей простотой. К его достоинствам также относится то, что он определяет, содержится ли в графе цикл с отрицательным весом, достижимый из истока. Алгоритм Дейкстры характеризуется меньшим временем выполнения, чем алгоритм Форда-Беллмана, и менее претезателен чем другие алгоритмы. Кроме того, приведен алгоритм динамического программирования — алгоритм Флойда-Уоршалла (Floyd-Warshall), который позволяет решить задачу о поиске кратчайших путей между всеми парами вершин, он очень прост в освоении и с него начинают изучение темы алгоритмов поиска кратчайшего пути, но у него очень низкая скорость работы и в нем не предусмотрен просчет ребер с отрицательным весом. | ||
| − | В итоге среди других алгоритмов выделяется алгоритм Дейкстры, у него больше всего достоинств и меньше всего недостатков | + | В итоге среди других алгоритмов выделяется алгоритм Дейкстры, у него больше всего достоинств и меньше всего недостатков, это: |
| + | +высокая скорость работы | ||
| + | +просчет ребер с отрицательным весом | ||
| + | +высокая точность результата | ||
| + | -сложность понимания | ||
[[Категория:ТГУ]] | [[Категория:ТГУ]] | ||
[[Категория:TEO2]] | [[Категория:TEO2]] | ||
Версия 21:27, 29 декабря 2011
Содержание |
Название проекта
Поиск кратчайшего пути
Авторы и участники проекта
Абашин Павел
Тема исследования группы
Преимущества и недостатки алгоритмов
Проблемный вопрос (вопрос для исследования)
Каковы преимущества и недостатки алгоритмов поиска кратчайшего пути?
Раскрытие вопроса
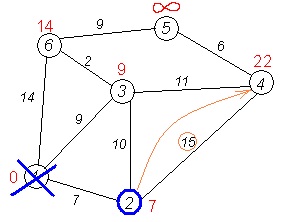
Кратчайший путь рассматривается при помощи некоторого математического объекта, называемого графом. Существуют несколько наиболее эффективных алгоритмов нахождения кратчайшего пути:
- алгоритм Дейкстры (используется для нахождения оптимального маршрута между двумя вершинами);
- алгоритм Форда-Беллмана;
- алгоритм Шимбелла.
Алгоритм Форда-Беллмана позволяет решить задачу о кратчайшем пути из фиксированного истока в общем случае, когда вес любого ребра может быть отрицательным. Этот алгоритм отличается своей простотой. К его достоинствам также относится то, что он определяет, содержится ли в графе цикл с отрицательным весом, достижимый из истока. Алгоритм Дейкстры характеризуется меньшим временем выполнения, чем алгоритм Форда-Беллмана, и менее претезателен чем другие алгоритмы. Кроме того, приведен алгоритм динамического программирования — алгоритм Флойда-Уоршалла (Floyd-Warshall), который позволяет решить задачу о поиске кратчайших путей между всеми парами вершин, он очень прост в освоении и с него начинают изучение темы алгоритмов поиска кратчайшего пути, но у него очень низкая скорость работы и в нем не предусмотрен просчет ребер с отрицательным весом.
В итоге среди других алгоритмов выделяется алгоритм Дейкстры, у него больше всего достоинств и меньше всего недостатков, это: +высокая скорость работы +просчет ребер с отрицательным весом +высокая точность результата -сложность понимания