Семинар ДООМ: Использование проблемных задач на уроках математики.
| Строка 1: | Строка 1: | ||
| − | + | [[Участник:Рыскалкина Наталья Васильевна]] | |
| + | |||
Основная задача общеобразовательной школы состоит не только в том, чтобы дать учащимся глубокие знания, но и в том, чтобы научить их самостоятельно решать проблемы, возникающие вокруг задачи, творчески мыслить. В основе проблемного обучения лежит учебная проблема, сущность которой является диалектическое противоречие между прежними знаниями ученика и новыми фактами, явлениями, для объяснения которых ранее приобретённых знаний недостаточно, нужны новые. Проблема должна быть такова, чтобы она соответствовала уровню возможностей учащихся. Кроме того, мастерство учителя заключается в том, чтобы создать проблемную ситуацию – побудить учащихся «принять проблему», «прочувствовать» потребность её решения. | Основная задача общеобразовательной школы состоит не только в том, чтобы дать учащимся глубокие знания, но и в том, чтобы научить их самостоятельно решать проблемы, возникающие вокруг задачи, творчески мыслить. В основе проблемного обучения лежит учебная проблема, сущность которой является диалектическое противоречие между прежними знаниями ученика и новыми фактами, явлениями, для объяснения которых ранее приобретённых знаний недостаточно, нужны новые. Проблема должна быть такова, чтобы она соответствовала уровню возможностей учащихся. Кроме того, мастерство учителя заключается в том, чтобы создать проблемную ситуацию – побудить учащихся «принять проблему», «прочувствовать» потребность её решения. | ||
| + | |||
Известный психолог С.Л. Рубинштейн говорил: «Мышление обычно начинается с проблемы или вопроса…». Приведу примеры проблемных задач, которые использую в своей работе. | Известный психолог С.Л. Рубинштейн говорил: «Мышление обычно начинается с проблемы или вопроса…». Приведу примеры проблемных задач, которые использую в своей работе. | ||
Версия 23:25, 16 ноября 2008
Участник:Рыскалкина Наталья Васильевна
Основная задача общеобразовательной школы состоит не только в том, чтобы дать учащимся глубокие знания, но и в том, чтобы научить их самостоятельно решать проблемы, возникающие вокруг задачи, творчески мыслить. В основе проблемного обучения лежит учебная проблема, сущность которой является диалектическое противоречие между прежними знаниями ученика и новыми фактами, явлениями, для объяснения которых ранее приобретённых знаний недостаточно, нужны новые. Проблема должна быть такова, чтобы она соответствовала уровню возможностей учащихся. Кроме того, мастерство учителя заключается в том, чтобы создать проблемную ситуацию – побудить учащихся «принять проблему», «прочувствовать» потребность её решения.
Известный психолог С.Л. Рубинштейн говорил: «Мышление обычно начинается с проблемы или вопроса…». Приведу примеры проблемных задач, которые использую в своей работе.
1)Тема : «Нахождение наибольшего и наименьшего значений».
Задача из рассказа Л.Н. Толстого. «Много ли человеку земли надо».
Крестьянин Пахом, который мечтал о собственной земле и собрал, наконец, желанную сумму, предстал перед требованием старшины: «Сколько за день земли отойдёт, вся твоя будет за 1000 рублей. Но если к заходу солнца не возвратишься на место, с которого вышел, пропали твои деньги».
Выбежал утром Пахом, прибежал на место и упал без чувств, обежав четырёхугольник периметром 40 км. Наибольшую ли площадь при данном периметре получил Пахом? При каких длинах сторон четырёхугольника периметром 40 км, его площадь будет наибольшей?
2)Тема: « Формула суммы первых членов геометрической прогрессии»
Индийский царь Шером позвал к себе изобретателя шахматной игры, своего подданного Сету, чтобы наградить его за остроумную выдумку. Сета попросил за первую клетку шахматной доски 1 зерно, за вторую – 2 зерна, за третью – 4 зерна и т.д. Обрадованный царь приказал выдать такую «скромную» награду. Однако, оказалось, что царь не в состоянии выполнить желание Сета. Почему такое количество зёрен?
3) Тема: « Наибольшее и наименьшее значение функции».
Из квадратного листа жести со стороной а надо изготовить открытую сверху коробку, вырезав по углам квадратики и загнуть образовавшиеся кромки. Какой должна быть сторона основания коробки, чтобы её объём был максимальным?
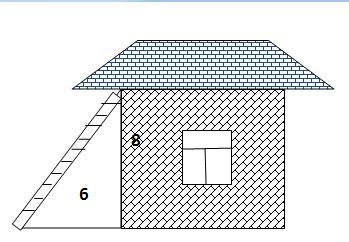
4)Тема: «Теорема Пифагора».
Задача. Найти длину лестницы, приставленной к дому, если один её конец находится на расстоянии 6 м от дома, а другой находится на стыке стены и крыши. Высота дома 8м. (Предлагается рассмотреть рисунок)