Семинар ДООМ Теорема о вписанном угле
| Строка 47: | Строка 47: | ||
Какими теоремами пользовались при нахождении угла? | Какими теоремами пользовались при нахождении угла? | ||
'''3. Введение определения вписанного угла.''' | '''3. Введение определения вписанного угла.''' | ||
| + | <gallery caption=''''Введение определения вписанного угла''''> | ||
| + | Изображение:Впис.3.3.JPG|Рис.3. | ||
| + | Изображение:Впис3.4.JPG|Рис.4. | ||
| + | Изображение:Впис3.5.JPG|Рис.5. | ||
| + | </gallery> | ||
| + | |||
Учитель: Сегодня познакомимся с новым понятием – вписанный угол. На рисунке 3 вы видите 2 вписанных угла, на рисунках 4 и 5 углы не являются вписанными. | Учитель: Сегодня познакомимся с новым понятием – вписанный угол. На рисунке 3 вы видите 2 вписанных угла, на рисунках 4 и 5 углы не являются вписанными. | ||
-Какой угол назовем вписанным? | -Какой угол назовем вписанным? | ||
| Строка 56: | Строка 62: | ||
-Хорды-отрезки, а стороны углов -лучи. | -Хорды-отрезки, а стороны углов -лучи. | ||
Далее учащиеся исправляют определение и произносят его полностью: | Далее учащиеся исправляют определение и произносят его полностью: | ||
| − | Угол, вершина которого лежит на окружности, а стороны пересекают окружность, называется вписанным углом. | + | '''Угол, вершина которого лежит на окружности, а стороны пересекают окружность, называется вписанным углом.''' |
Версия 12:45, 29 ноября 2009
Участник: Молдагалиева Дамира Ароновна Тема урока: Теорема о вписанном угле.
5 –ый урок в главе 8 «Окружность», 2 урок в теме «Центральные и вписанные углы».
Тип урока: введение нового материала. Оборудование: интерактивная доска, транспортир, угольник, линейка Цели урока: • Обучения: ввести и закрепить определение вписанного угла, сформулировать теорему о вписанном угле, получить вместе с учащимися доказательство теоремы и закрепить его. • Развития: учить осознавать на отдельных примерах правила образования определений, обучать на примерах подведению под определение, обратить внимание на метод доказательства - рассмотрение всех частных случаев. • Воспитания: воспитание аккуратности (аккуратное выполнение чертежей на доске и в тетрадях, рациональное распределение записей), рациональное распределение времени, критичности.
Структура урока:
1. Организационный момент. (2 минуты) 2. Подготовка к изучению нового материала.(6 минут) 3. Введение определение вписанного угла. (5 минут) 4. Доказательство теоремы о вписанном угле. (15 минут) 5. Закрепление формулировки теоремы. (10 минут) 6. Подведение итогов урока. Ход урока:
1.Организационный момент.
Приветствие, сообщение темы и задач урока. Сегодня изучим новые понятия вписанного угла, свойство вписанного угла, а также повторим старый материал, который потребуется для изучения нового.
2. Подготовка к изучению нового материала.(6 минут).
Для всего класса: Тест.(4 мин) (с последующей проверкой).
Индивидуально у доски ( в это же время) проверка домашнего задания №652.
( заранее учителем готовится решение на интерактивной доске и скрывается за «шторкой». После выполнения всем классом теста, проверяется правильность выполнения домашнего задания.
- Проверка домашнего задания №652
Устная фронтальная работа:
• сформулировать теорему о сумме углов треугольника.
• сформулировать теорему о внешнем угле треугольника.
• Решить задачи
- Решение задач
Какими теоремами пользовались при нахождении угла?
3. Введение определения вписанного угла.
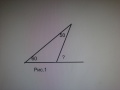
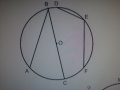
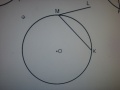
Учитель: Сегодня познакомимся с новым понятием – вписанный угол. На рисунке 3 вы видите 2 вписанных угла, на рисунках 4 и 5 углы не являются вписанными.
-Какой угол назовем вписанным?
-Предположительный ответ: Если вершина лежит на окружности.
-Но ведь и на рисунке 5 вершина угла лежит на окружности, однако он не является вписанным.
-Предположительный ответ: Если стороны углов касаются окружности. -На рисунке 3 стороны углов касаются окружности? - Предположительный ответ: Стороны являются хордами. -Хорды-отрезки, а стороны углов -лучи. Далее учащиеся исправляют определение и произносят его полностью: Угол, вершина которого лежит на окружности, а стороны пересекают окружность, называется вписанным углом.