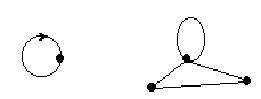Семинар ДООМ Некоторые уточнения для лучшего взаимопонимания

Версия 21:35, 22 ноября 2007

Или дополнения к предложенному теоретическому материалу, призванные для уточнения значения некоторых терминов и понятий.

Коннова Елена Генриевна ID_062,ID_063

Участник:Коннова_Елена

При решении задач обучающего тура многие команды заметили ошибку в решении задачи 8 (некоторые писали об этом в отчете, другие видимо сочли опечаткой и постеснялись). Я думаю, если бы эта ошибка была напечатана в решениях специально, организаторам ДООМ нужно было бы поставить оценку «6» за проделанную работу. Найденная ошибка резко повысила самооценку ребят, особенно тех, кто сам с задачами справился не очень успешно. Кроме этого, был приобретен очень ценный опыт вдумчивого и критического чтения текстов. Участники обсуждения стали не просто читать и слушать чужие решения, но и вдумываться в них, задавать вопросы, что явно способствует лучшему пониманию. Так что спасибо тем, кто «придумал» такую ошибку.

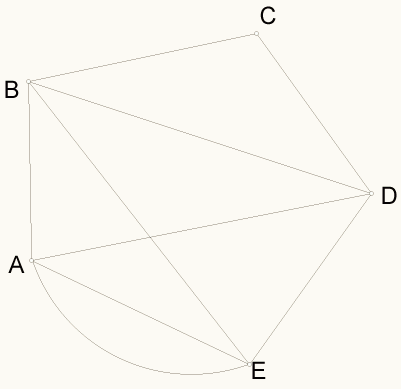
После этого вернулись к задаче 2 обучающего тура и поняли, что ее решение не такое очевидное, как кажется. В задаче утверждается, что невозможно построить граф с пятью вершинами степенями 4, 4, 4, 4, 2. Вместе с тем, очевидно, что такой граф существует.

В приведенном решении, видимо, предполагается, что две вершины графа можно соединить только одним ребром. Обратимся к « Математическому энциклопедическому словарю», Москва, 1995.

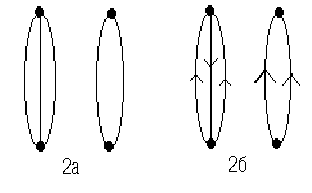
Пара вершин графа может соединяться двумя или более ребрами (или дугами одинакового направления, если граф ориентированный), тогда они называются кратными (Рис. 2а, б).

Ребро (или дуга) может начинаться и заканчиваться в одной вершине, такое ребро называется петлей (рис.3).

Видимо, в задаче 2 нужно было оговорить, что в графе нет ни кратных ребер, ни петель. Тогда решение будет очевидным.

Коннова Елена 22:33, 22 ноября 2007 (UZT)