Семинар ДООМ "Математическое исследование "Кенигсбергские мосты"
| Строка 1: | Строка 1: | ||
| + | [[Участник: Шувалова Юлия Григорьевна|Автор:Шувалова Юлия Григорьевна]] | ||
| + | |||
'''ОПРЕДЕЛЕНИЕ:''' Граф, который можно нарисовать, не отрывая карандаша от бумаги и проводя каждое ребро один раз, называется эйлеровым или уникурсальным. | '''ОПРЕДЕЛЕНИЕ:''' Граф, который можно нарисовать, не отрывая карандаша от бумаги и проводя каждое ребро один раз, называется эйлеровым или уникурсальным. | ||
| Строка 19: | Строка 21: | ||
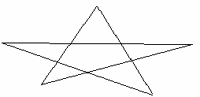
h) Проверь свою гипотезу на примере (В первом случае: вершины графа – вершины звезды, во втором – точки пересечения ребер) | h) Проверь свою гипотезу на примере (В первом случае: вершины графа – вершины звезды, во втором – точки пересечения ребер) | ||
| + | |||
[[Изображение:graf7.jpg]] | [[Изображение:graf7.jpg]] | ||
| Строка 37: | Строка 40: | ||
h) Повтори несколько раз. Сделай вывод. | h) Повтори несколько раз. Сделай вывод. | ||
| + | |||
[[Изображение:graf8.jpg]] | [[Изображение:graf8.jpg]] | ||
3. Построй граф, соответствующий задаче о кенигсбергских мостах. Берега обозначь буквами А и В, острова – С и D. Ребрами графа будут мосты, соеди-няющие соответствующие участки берегов и островов. Объясни, каким образом Эйлер мог показать, что эта задача не имеет решения. | 3. Построй граф, соответствующий задаче о кенигсбергских мостах. Берега обозначь буквами А и В, острова – С и D. Ребрами графа будут мосты, соеди-няющие соответствующие участки берегов и островов. Объясни, каким образом Эйлер мог показать, что эта задача не имеет решения. | ||
Версия 12:20, 4 декабря 2007
Автор:Шувалова Юлия Григорьевна
ОПРЕДЕЛЕНИЕ: Граф, который можно нарисовать, не отрывая карандаша от бумаги и проводя каждое ребро один раз, называется эйлеровым или уникурсальным.
Задание:
1. a) Отметь на листе бумаги произвольную точку А.
b) Не отрывая карандаша от бумаги, проведи произвольную кривую так, чтобы она начиналась и заканчивалась в точке А.
c) Точки пересечения построенной линии и точку А примем за вершины графа. Ясно, что полученный граф является уникурсальным.
d) Определи, сколько раз при этом заходили в вершину и выходили из нее (причем по другому ребру).
e) Сосчитай сколько раз необходимо зайти в каждую из вершин (число «входов»), и сколько раз выйти из нее по другому ребру (число «выходов»), чтобы пройти по каждому ребру и вернуться в исходную вершину.
f) Определи степени вершин полученного графа и их вид (четные или нечетные).
g) Повтори несколько раз. Сделай вывод
h) Проверь свою гипотезу на примере (В первом случае: вершины графа – вершины звезды, во втором – точки пересечения ребер)
2. a) Отметь на листе бумаги произвольные точки А и В.
b) Не отрывая карандаша от бумаги, проведи произвольную кривую так, чтобы она начиналась в точке А и заканчивалась в точке В.
c) Точки пересечения построенной линии и точки А, В примем за вершины графа. Ясно, что полученный граф является уникурсальным.
d) Определи степени вершин полученного графа и их вид (четные или нечетные).
e) Какую степень должны иметь эти две вершины? Что можно сказать о числе «входов» и числе «выходов» для каждой вершины.
f) Какую степень должны иметь остальные вершины?
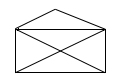
g) Сделай вывод и проверь на примере (вершины графа – точки пересечения ребер)
h) Повтори несколько раз. Сделай вывод.
3. Построй граф, соответствующий задаче о кенигсбергских мостах. Берега обозначь буквами А и В, острова – С и D. Ребрами графа будут мосты, соеди-няющие соответствующие участки берегов и островов. Объясни, каким образом Эйлер мог показать, что эта задача не имеет решения.