Семинар ДООМ Теория графов и оптимизация
| Строка 1: | Строка 1: | ||
'''Теория графов и оптимизация''' | '''Теория графов и оптимизация''' | ||
| − | + | '''Команда 061''' | |
| + | --[[Участник:Москевич Лариса Вячеславовна|Москевич Лариса Вячеславовна]] 20:53, 7 декабря 2007 (UZT) | ||
В последнее время в школах стали большое внимание уделять проектной и исследовательской работе учащихся. Очень сложно порой выбрать тему проекта по математике, учитывая пожелание, чтобы работа учащегося носила не просто реферативный, а исследовательский характер, имела практическую направленность. | В последнее время в школах стали большое внимание уделять проектной и исследовательской работе учащихся. Очень сложно порой выбрать тему проекта по математике, учитывая пожелание, чтобы работа учащегося носила не просто реферативный, а исследовательский характер, имела практическую направленность. | ||
| Строка 20: | Строка 21: | ||
'''Задача о кратчайшем пути.''' | '''Задача о кратчайшем пути.''' | ||
| − | + | Как кратчайшим путем (и, следовательно, с наименьшим расходом топлива и времени, наиболее дешево) попасть из пункта А в пункт Б? Иначе эта задача звучит: « Как кратчайшим путем попасть из одной вершины графа в другую». | |
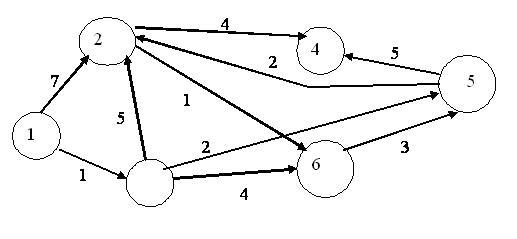
Для решения этой задачи каждой дуге ориентированного графа должно быть сопоставлено число - время движения по этой дуге от начальной вершины до конечной. Рассмотрим пример: как кратчайшим путем попасть из вершины 1 в вершину 4? | Для решения этой задачи каждой дуге ориентированного графа должно быть сопоставлено число - время движения по этой дуге от начальной вершины до конечной. Рассмотрим пример: как кратчайшим путем попасть из вершины 1 в вершину 4? | ||
| Строка 30: | Строка 31: | ||
Решение. Введем обозначение: С(Т) - длина кратчайшего пути из вершины 1 в вершину Т. (Поскольку любой путь, который надо рассмотреть, состоит из дуг, а дуг конечное число, и каждая входит не более одного раза, то претендентов на кратчайший путь конечное число, и минимум из конечного числа элементов всегда достигается.) | Решение. Введем обозначение: С(Т) - длина кратчайшего пути из вершины 1 в вершину Т. (Поскольку любой путь, который надо рассмотреть, состоит из дуг, а дуг конечное число, и каждая входит не более одного раза, то претендентов на кратчайший путь конечное число, и минимум из конечного числа элементов всегда достигается.) | ||
| − | + | Рассматриваемая задача состоит в вычислении С(4) и указании пути, на котором этот минимум достигается. | |
Для исходных данных, представленных на рис. в вершину 3 входит только одна стрелка, как раз из вершины 1, и около этой стрелки стоит ее длина, равная 1, поэтому С(3) = 1. Кроме того, очевидно, что С(1) = 0. | Для исходных данных, представленных на рис. в вершину 3 входит только одна стрелка, как раз из вершины 1, и около этой стрелки стоит ее длина, равная 1, поэтому С(3) = 1. Кроме того, очевидно, что С(1) = 0. | ||
Версия 20:07, 7 декабря 2007
Теория графов и оптимизация
Команда 061
--Москевич Лариса Вячеславовна 20:53, 7 декабря 2007 (UZT) В последнее время в школах стали большое внимание уделять проектной и исследовательской работе учащихся. Очень сложно порой выбрать тему проекта по математике, учитывая пожелание, чтобы работа учащегося носила не просто реферативный, а исследовательский характер, имела практическую направленность.
Одним из направлений таких исследований можно выбрать проблему оптимизации. Такие задачи имеют большое значение в практической жизни.
К задачам оптимизации сводятся многие задачи выбора наиболее экономичного (с точки зрения расстояния или времени или стоимости) маршрута на имеющейся карте дорог. В математике разработан ряд методов для решения подобных задач. Но часто методы, основанные на использовании графов, оказываются наименее трудоемкими, а для учащихся школы и более наглядными и понятными.
Рассмотрим несколько типичных задач принятия решений, связанных с оптимизацией на графах.
Задача коммивояжера. Требуется посетить все вершины графа и вернуться в исходную вершину, минимизировав затраты на проезд (или минимизировав время). сходные данные здесь - это граф, дугам которого приписаны положительные числа -атраты на проезд или время, необходимое для продвижения из одной вершины в другую. В общем случае граф является ориентированным, и каждые две вершины соединяют две дуги - туда и обратно. Действительно, если пункт А расположен на горе, а пункт Б - в низине, то время на проезд из А в Б, очевидно, меньше времени на обратный проезд из Б в А.
Многие задачи экономического содержания сводятся к задаче коммивояжера. Например: составить наиболее выгодный маршрут обхода наладчика в цехе (контролера, охранника, милиционера), отвечающего за должное функционирование заданного множества объектов (каждый из этих объектов моделируется вершиной графа); составить наиболее выгодный маршрут доставки деталей рабочим или хлеба с хлебозавода по заданному числу булочных и других торговых точек (парковка у хлебозавода).
Задача о кратчайшем пути.
Как кратчайшим путем (и, следовательно, с наименьшим расходом топлива и времени, наиболее дешево) попасть из пункта А в пункт Б? Иначе эта задача звучит: « Как кратчайшим путем попасть из одной вершины графа в другую».
Для решения этой задачи каждой дуге ориентированного графа должно быть сопоставлено число - время движения по этой дуге от начальной вершины до конечной. Рассмотрим пример: как кратчайшим путем попасть из вершины 1 в вершину 4?
Исходные данные к задаче о кратчайшем пути.
Решение. Введем обозначение: С(Т) - длина кратчайшего пути из вершины 1 в вершину Т. (Поскольку любой путь, который надо рассмотреть, состоит из дуг, а дуг конечное число, и каждая входит не более одного раза, то претендентов на кратчайший путь конечное число, и минимум из конечного числа элементов всегда достигается.)
Рассматриваемая задача состоит в вычислении С(4) и указании пути, на котором этот минимум достигается.
Для исходных данных, представленных на рис. в вершину 3 входит только одна стрелка, как раз из вершины 1, и около этой стрелки стоит ее длина, равная 1, поэтому С(3) = 1. Кроме того, очевидно, что С(1) = 0.
В вершину 4 можно попасть либо из вершины 2, пройдя путь, равный 4, либо из вершины 5, пройдя путь, равный 5. Поэтому справедливо соотношение
С(4) = min {С(2) + 4 ; С(5) + 5}.
Таким образом, проведена реструктуризация задачи - нахождение С(4) сведено к нахождению С(2) и С(5).
В вершину 5 можно попасть либо из вершины 3, пройдя путь, равный 2, либо из вершины 6, пройдя путь, равный 3. Поэтому справедливо соотношение
С(5) = min {С(3) + 2 ; С(6) + 3}.
Мы знаем, что С(3) = 1. Поэтому С(5) = min {3 ; С(6) + 3}.
Поскольку очевидно, что С(6) - положительное число, то из последнего соотношения вытекает, что С(5) = 3.
В вершину 2 можно попасть либо из вершины 1, пройдя путь, равный 7, либо из вершины 3, пройдя путь, равный 5, либо из вершины 5, пройдя путь, равный 2. Поэтому справедливо соотношение
С(2) = min {С(1) + 7 ; С(3) + 5 ; С(5) + 2}.
Нам известно, что С(1) = 0, С(3) = 1, С(5) = 3.
Поэтому С(2) = min {0 + 7 ; 1 + 5 ; 3 + 2} = 5.
Теперь мы можем найти С(4):
С(4) = min {С(2) + 4 ; С(5) + 5} = min {5 + 4 ; 3 + 5} = 8.
Таким образом, длина кратчайшего пути равна 8. Из последнего соотношения ясно, что в вершину 4 надо идти через вершину 5.
Возвращаясь к вычислению С(5), видим, что в вершину 5 надо идти через вершину 3. А в вершину 3 можно попасть только из вершины 1. Итак, кратчайший путь таков:
1 → 3 → 5 → 4 .
Задача о кратчайшем пути для конкретных исходных данных полностью решена.
Оптимизационные задачи на графах, возникающие при подготовке управленческих решений в производственном менеджменте, весьма многообразны.
Рассмотрим в качестве примера еще одну задачу, связанную с перевозками.
Задача о максимальном потоке.
Как (т.е. по каким маршрутам) послать максимально возможное количество грузов из начального пункта в конечный пункт, если пропускная способность путей между пунктами ограничена?
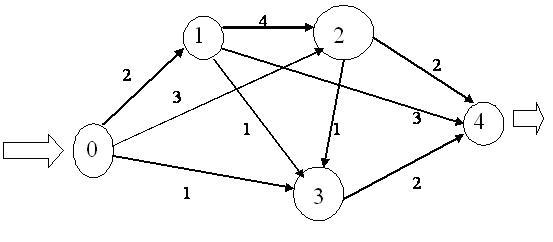
Для решения этой задачи каждой дуге ориентированного графа, соответствующего транспортной системе, должно быть сопоставлено число - пропускная способность этой дуги. Рассмотрим пример
Решение задачи о максимальном потоке может быть получено из следующих соображений. Очевидно, максимальная пропускная способность транспортной системы не превышает 6, поскольку не более 6 единиц грузов можно направить из начального пункта 0, а именно, 2 единицы в пункт 1, 3 единицы в пункт 2 и 1 единицу в пункт 3.
Далее надо добиться, чтобы все 6 вышедших из пункта 0 единиц груза достигли конечного пункта 4. Очевидно, 2 единицы груза, пришедшие в пункт 1, можно непосредственно направить в пункт 4. Пришедшие в пункт 2 грузы придется разделить: 2 единицы сразу направить в пункт 4, а 1 единицу - в промежуточный пункт 3 (из-за ограниченной пропускной способности участка между пунктами 2 и 4).
В пункт 3 доставлены такие грузы: 1 единица из пункта 0 и 1 единица из пункта 3. Их направляем в пункт 4.
Итак, максимальная пропускная способность рассматриваемой транспортной системы -6 единиц груза. При этом не используются внутренние участки (ветки) между пунктами 1 и 2, а также между пунктами 1 и 3. Не догружена ветка между пунктами 1 и 4 - по ней направлены 2 единицы груза при пропускной способности в 3 единицы.
Задачи оптимизации можно конкретизировать для определенных жизненных ситуаций. Учащийся старшего звена вполне способен справиться с данной работой.