Семинар ДООМ "Игра Счастливый случай"
| Строка 57: | Строка 57: | ||
Поменяйте их местами | Поменяйте их местами | ||
| − | [[Изображение: | + | [[Изображение:qq2.gif]] |
(т.е. чтобы в верхних углах оказались белые кони, а в нижних - черные), сколько ходов для этого необходимо? | (т.е. чтобы в верхних углах оказались белые кони, а в нижних - черные), сколько ходов для этого необходимо? | ||
| Строка 77: | Строка 77: | ||
- Нет, Городничим буду я, - хором закричали Алик и Боря, - или Хлестаковым, - добавили они одновременно. | - Нет, Городничим буду я, - хором закричали Алик и Боря, - или Хлестаковым, - добавили они одновременно. | ||
Удастся ли ребятам распределить роли так, чтобы все были довольны? | Удастся ли ребятам распределить роли так, чтобы все были довольны? | ||
| − | [[Изображение:qq3. | + | [[Изображение:qq3.gif]] |
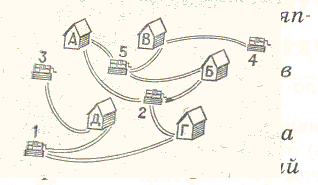
5. Жители пяти домов поссорились друг с другом и , чтобы не встречаться у колодцев, решили поделить их ( колодцы) так, чтобы хозяин каждого дома ходил к «своему» колодцу по «своей» тропинке. Удастся ли это сделать? | 5. Жители пяти домов поссорились друг с другом и , чтобы не встречаться у колодцев, решили поделить их ( колодцы) так, чтобы хозяин каждого дома ходил к «своему» колодцу по «своей» тропинке. Удастся ли это сделать? | ||
| − | [[Изображение: | + | [[Изображение:qq4.gif]] |
6. Муха забралась в банку из-под сахара. Банка имеет форму куба. Сможет ли муха последовательно обойти все 12 ребер куба, не проходя дважды по одному ребру. Подпрыгивать и перелетать с места на место не разрешается. (Невозможен) | 6. Муха забралась в банку из-под сахара. Банка имеет форму куба. Сможет ли муха последовательно обойти все 12 ребер куба, не проходя дважды по одному ребру. Подпрыгивать и перелетать с места на место не разрешается. (Невозможен) | ||
| Строка 86: | Строка 86: | ||
Решение: | Решение: | ||
| − | [[Изображение:Qq5. | + | [[Изображение:Qq5.gif]] |
| Строка 120: | Строка 120: | ||
Ответ: | Ответ: | ||
2. Расставить 12 стульев тремя рядами так, чтобы в каждом ряду было по 5 стульев. | 2. Расставить 12 стульев тремя рядами так, чтобы в каждом ряду было по 5 стульев. | ||
| − | + | Ответ: | |
Версия 17:27, 14 декабря 2007
Урок игра «Счастливый случай» для 6-7 классов Цели: развивать дух коллективизма, смекалку, логику и внимательность; воспитывать уверенность и умение быстро сосредоточиться на главном; развивать интерес к математике. Ведущий: Добрый день, дорогие друзья. Сегодня мы мы поиграем в интересную игру «Счастливый случай». Темой нашего обсуждения являются «Графы». Давайте разделимся на 2 команды I. Гейм «Разминка».Каждой команде задается по 14 вопросов, на которые ученики отвечают без обсуждения. Право ответа распределяет капитан команды, ответ может быть только один. Если команда отвечает неверно, право ответить на этот вопрос переходит к команде соперников. За каждый правильный ответ на свой вопрос команда получает 2 балла, за каждый правильный ответ на вопрос соперников команда получает 1 балл. Вопросы первой команде: 1.Что такое графы?
2. Кто является родоначальником теории графов?
3. Какую задачу решал Леонард Эйлер?
4. Какие бывают графы?
5.Как. ие буквы русского алфавита можно нарисовать одним росчерком?
6. Буквы М и Ш уникурсальны?
7. Является ли графом географическая карта?
8. Сколько ребер имеет нулевой граф с 7 вершинами?
9. Какая фигура не уникурсальна?
10. Граф имеет 6 вершин. Сколько ребер выходит из каждой вершины?
Вопросы второй команде: 1. Какой граф называется плоским?
2. Что такое цикл в графах?
3. Какие бывают циклы?
4. Что необходимо чтобы граф был Эйлеровым?
5 Дайте определение нуль - графы.
6. Буквы Т и Ш уникурсальны?
7. Является ли графом множество городов и соединяющие их дороги?
8. Сколько ребер имеет нулевой граф с 15 вершинами?
9.. Каким числом всегда является сумма степеней вершин графа?
10. Граф имеет 11 вершин. Сколько ребер выходит из каждой вершины?
II. Гейм «3аморочки из бочки». В мешочке находится 9 бочонков. Каждому бочонку соответствует задача. Команды по очереди вытаскивают бочонок и слушают условие задачи. На обдумывание дается 30 секунд, затем команда дает ответ. За правильный ответ команда получает 3 балла. Если же ответ неверный, то право ответа переходит другой команде, которая может получить дополнительно только 1 балл. В этом гейме у команд есть возможность испытать удачу, задачи соответствуют только 8 бочонкам, а если вытащенный бочонок с номером 9, то команда без решения зарабатывает 3 балла.
Задачки- заморочки:
1. Трое играли в шашки. Всего сыграли три партии. Сколько партий сыграл каждый? (2 партии)
2. В очереди стоят Юра, Миша, Вова, Саша и Олег. Юра стоит раньше Миши, но после Олега. Вова и Олег не стоят рядом. Саша не стоит рядом ни с Олегом, ни с Юрой, ни с Вовой. В каком порядке стоят ребята?(Олег, Юра, Вова, Миша, Саша)
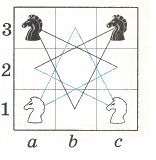
3. В верхних углах доски 3х3 стоят черные кони, в нижних- белые
Поменяйте их местами
(т.е. чтобы в верхних углах оказались белые кони, а в нижних - черные), сколько ходов для этого необходимо?
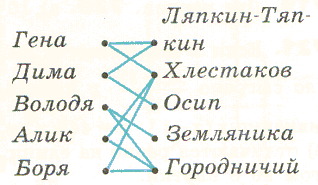
4. В школьном драмкружке решили ставить «Ревизора», и тут разгорелся спор.
- Ляпкиным- Тяпкиным буду я,- заявил Гена.
- Нет, я ! Я вся жизнь мечтал воплотить этот образ, - возразил Дима.
- Хорошо, я уступлю, если мне дадут роль Хлястакова, проявил великодушие Гена.
- А мне Осипа, - не уступил в великодушии Дима.
- Хочу быть Земляникой или Городничем, - сказал Володя.
- Нет, Городничим буду я, - хором закричали Алик и Боря, - или Хлестаковым, - добавили они одновременно.
Удастся ли ребятам распределить роли так, чтобы все были довольны?
 5. Жители пяти домов поссорились друг с другом и , чтобы не встречаться у колодцев, решили поделить их ( колодцы) так, чтобы хозяин каждого дома ходил к «своему» колодцу по «своей» тропинке. Удастся ли это сделать?
5. Жители пяти домов поссорились друг с другом и , чтобы не встречаться у колодцев, решили поделить их ( колодцы) так, чтобы хозяин каждого дома ходил к «своему» колодцу по «своей» тропинке. Удастся ли это сделать?
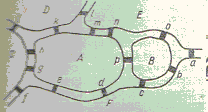
6. Муха забралась в банку из-под сахара. Банка имеет форму куба. Сможет ли муха последовательно обойти все 12 ребер куба, не проходя дважды по одному ребру. Подпрыгивать и перелетать с места на место не разрешается. (Невозможен) 7. Можно ли совершить прогулку по городу, план которого показан на рис. , пройдя в точности один раз по каждому из пятнадцати мостов? Решение:
8. На острове Буяне четыре государства, каждое из которых граничит с тремя другими. Нарисуйте карту острова. Ответ: Возможны следующие варианты.
III. Гейм «Темная лошадка». Следующий гейм называется «Темная лошадка». Его проведет учитель, который в течение всего учебного года заботится о вас. помогает вам, часто видится с вашими родителями и многие праздники вы проводите вместе с ним. Приглашается классный руководитель. Тем, кто угадал, кого пригласили, прибавляется 1 балл. Классный руководитель раздает по задаче каждой команде. За правильный ответ прибавляется еще по 2 балла. Задачи для 1 команды:
1. Не отрывая карандаша от бумаги и не проводя ни по какому ребру дважды, нарисуйте граф, изображенный на рисунке Пронумеруйте ребра в той последовательности, в которой вы их проходили. Ответ:
2. Расставьте 10 стульев вдоль стен прямоугольной комнаты так, чтобы возле каждой стены стульев было поровну. Ответ:
Задачи для 2 команды:
1. Не отрывая карандаша от бумаги и не проводя ни по какому ребру дважды, нарисуйте граф, изображенный на рисунке Занумеруйте ребра в той последовательности, в которой вы их проходили. Ответ: 2. Расставить 12 стульев тремя рядами так, чтобы в каждом ряду было по 5 стульев. Ответ:
Затем подсчитываются баллы за проведенные конкурсы.
IV. Гейм «Ты - мне, я - тебе». После ответов обеих команд подсчитываются баллы. А теперь пришла пора показать себя капитанам команд. Каждый из них может задать другому капитану по два вопроса. Отвечать могут только капитаны. Если на вопрос ответил правильно, то получает 2 балла тот, кто отвечал. Если же ответ неверный, то 1 балл зарабатывает капитан, который задавал вопрос, но только после того, как сам расскажет правильный ответ. Подсчитываются баллы. Примерные задачи: 1. Задача Леонардо Эйлера. Можно ли поочередно обойти все семь мостов города Кенигсберга, соединяющих районы этого города с островами на реке Преголя, проходя по каждому мосту только один раз.
2. Экскурсоводу нужно выбрать маршрут по залам музея так, чтобы обойти все залы, не проходя ни через одну дверь дважды. Где нужно начать и где закончить осмотр? Найдите один из возможных маршрутов.
3. Крестьянину нужно перевести через реку волка, козу и капусту. Но лодка такова, что в ней может поместиться крестьянин, а с ним или только волк, или только коза, или только капуста. Но если оставить волка с козой, то волк съест козу, а если оставить козу с капустой, то коза съест капусту. Как перевести свой груз крестьянину?
V. Гейм «Гонка за лидером». Вопросы последнего гейма сначала задаются команде, которая проигрывает. Время на ответы - 1 минута. Если команда не знает ответа, то просит следующий вопрос. Сколько вопросов будет зачитано, зависит только от команды.
Вопросы первой команде:
1. Графом называется …?
2.Какое число нечетное 5 или 17?
3. Буквы Л и О уникурсальны?
4. Сколько вершин графа соединяет одно ребро?
5. Является ли графом схема автомобильных дорог?
6.Сколько ребер имеет нулевой граф с 5 вершинами?
7.Граф имеет 6 вершин. Сколько ребер выходит из каждой вершины?
8. Вершиной графа называется?
9. Какое число четное 8 или 7?
Вопросы второй команде: 1. Ребром графа называется…?
2. Какое число нечетное 6 или 12?
3. Уникурсальная фигура это …?
4. Буквы О и Д уникурсальны - …
5.Является ли графом схема метрополитена?
6.Сколько ребер имеет нулевой граф с 4 вершинами?
7.Граф имеет 8 вершин. Сколько ребер выходит из каждой вершины? 8. Степенью вершины графа называется?
9. Какое число четное 3 или 10?
Затем подсчитываются баллы за проведенные конкурсы.
VI. Подведение итогов. После подсчета баллов определяется победитель, который получает приз. Но также можно выделить в каждой команде самого активного игрока и их поздравить отдельно.