Семинар ДООМ Уникурсальные кривые (фигуры)

Текущая версия на 14:55, 10 января 2008

Автор: Невзорова Марина Евгеньевна

ID команды: 002

Конспект урока по теме: «Уникурсальные кривые (фигуры)».

Класс: 6

Цели урока:

Обобщить и систематизировать знания по данной теме;
заинтересовать учеников дополнительным материалом;
развивать начала математического мышления,
расширить кругозор, пробудить желание заниматься изучением математики.

Ход урока.

1.Постановка проблемы.

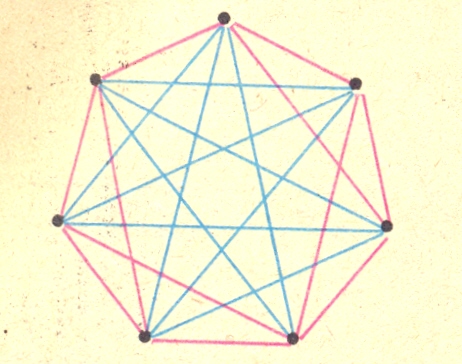
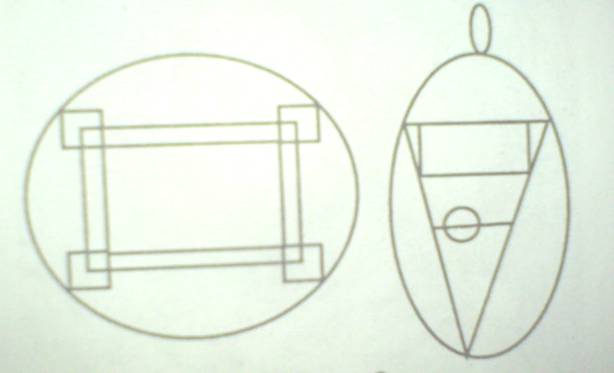
Начертите каждую из фигур, изображенных на рис.1, не отрывая карандаша от бумаги и не проводя более раза по одной и той же линии.

Многие начинают с фигуры г, однако все попытки нарисовать ее одним росчерком не удается.

С меньшей уверенностью ученики приступают к остальным фигурам. Без больших затруднений справляются с фигурами а и б, в. Но фигуры г и д никому не удалось нарисовать.

Нельзя ли указать какой–нибудь признак, по которому можно было заранее судить о том, можно ли нарисовать конкретную фигуру одним росчерком или нет?

2.Изучение нового материала.

Назовем каждый перекресток, в котором сходятся линии данной фигуры, узлом: четным, если в нем сходится четное число линий, и нечетным, если число сходящихся в нем линий нечетное. На фигуре а все узлы четные, на б два нечетных ( А и В) и четыре четных(С,D,E,F) узла, на фигуре в нечетными узлами являются точки А,В; на фигурах г и д по четыре нечетных узла.

В фигуре а все узлы четные. Фигуру б с двумя нечетными узлами А и В тоже можно начертить одним росчерком.

Начнем обход с одного нечетного узла и пройдем по какой–нибудь линии до другого нечетного узла, например по АСВ. Тем самым мы исключили по одной линии из каждого нечетного узла. В результате оба нечетных узла стали четными, и мы фигуру с четными узлами(треугольник BDA с окружностью), которую можно начертить.

Итак, если фигура содержит два нечетных узла, то успешный росчерк должен начинаться в одном из них и заканчиваться в другом. Если фигура имеет четыре нечетных узла, то ее можно нарисовать двумя росчерками (г и д).

Фигуры а-в называются уникурсальные.

Вывод:

1)в уникурсальной кривой может быть любое число четных узлов, но не более двух четных;

2)если в фигуре только четные узлы, то обход можно начинать с любой точки;

3)если в фигуре два нечетных узла, то обход нужно начинать с одного из них, а заканчивать- в другом нечетном узле.

3.Решение задач.

Задание 1. Какие фигуры русского алфавита можно нарисовать одним росчерком?

Ответ: Б,В,Г,З,И,Л,М,О,П,Р,С,Ф,Ъ,Ь,Я.

Задание 2.Начертите каждую из фигур одним росчерком .

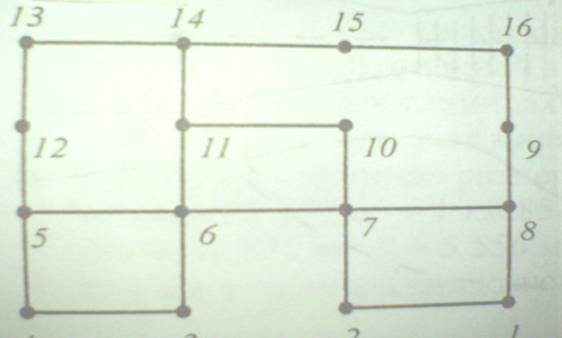
Задание 3. На рисунке приведен план подземного лабиринта (подвала из 16 комнат, соединенных дверями.) Можно ли, начиная с комнаты 1, обойти комнаты так, чтобы пройти все двери комнат только один раз? В какой комнате закончиться обход?

Решение:

Заменим комнаты точками, а двери-отрезками.

Так как у нас два нечетных узла 1 и 5, то данная фигура является уникурсальной. Значит, можно, начиная с одного нечетного узла (1), обойдя все узлы по одному разу, прийти в другой нечетный узел (5).

Ответ: можно, закончив обход в комнате 5 (смотри рисунок).

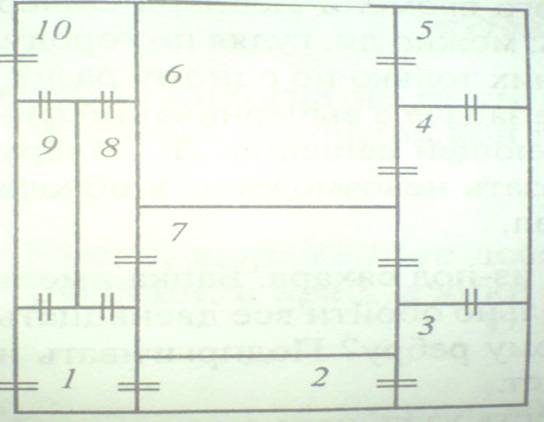
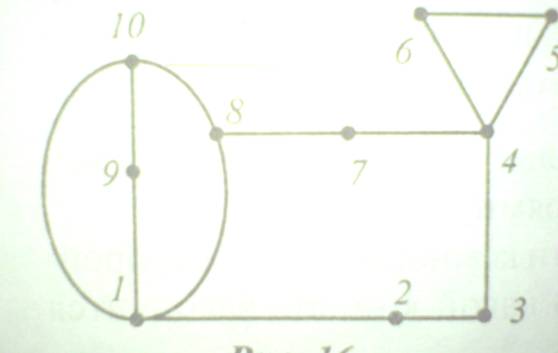
Задача 4. На рисунке изображен план подвала из десяти комнат. Можно ли пройти через все двери всех комнат, запирая каждый раз дверь, через которую вы проходите? С какой комнаты надо начать движение?

Решение:

Заменяя комнаты точками, а двери-дугами, отрезками, получим фигуру с двумя нечетными узлами 8 и 10 значит, она является уникурсальной, т. е. можно пройти через все двери комнат, запирая каждый раз ту, через которую прошли.

Ответ: можно, начав движение с комнаты 8 или 10.

4.Подведение итогов урока.

5.Творческое домашнее задание.

Придумать задачу по данной теме и оформить ее решение творческим способом.