Семинар ДООМ урок математики "Графы"
| Строка 186: | Строка 186: | ||
<h3> '''Д.з. Дополнить схему примерами применения графов'''</h3> | <h3> '''Д.з. Дополнить схему примерами применения графов'''</h3> | ||
| − | [[Категория:Проект ДООМ]] | + | [[Категория:Проект ДООМ 2007-2008 (1 цикл)]] |
Текущая версия на 14:59, 10 января 2008
Участник:Октысюк Ульяна Святославовна Группа 069
Содержание[убрать] |
Урок: Модели знаний на графах
Сегодня на уроке мы будем открывать и исследовать новую для вас страницу «Модели знаний на графах» и научимся использовать графы в различных жизненных ситуациях.
Форма проведения: групповая работа
Цели:
- Знание: Ученик знает назначение графов
-Понимание: Умеет приводить примеры использования графов в различных учебных предметах (химия, информатика, биология, геометрия и др.) и повседневной жизни.
-Применение: Умеет записывать арифметические выражения в виде графов, отражать информацию в виде семантической сети, изображать классификации разл. объектов в виде дерева -Анализ: Умеет из множества предметов вычленить объекты, обозначить связи между ними.
Синтез: Умеет делать выводы о значении науки информатики для остальных школьных предметов/
Оборудование: мультимедийный компьютер, кодоскоп, таблицы.
План урока
1. Понятие графа.
2. Семантические сети.
3. Представление информации в виде дерева.
4. Анализ смысла математических выражений.
5. Подведение итогов урока.
Ход урока
I. Вступительная беседа
О, сколько нам открытий чудных
Готовит просвещенья дух…
А.С. Пушкин
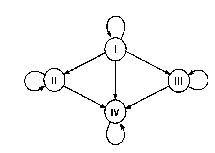
Сегодня на уроке мы будем открывать, и исследовать новую для вас страницу «Модели знаний на графах» и научимся использовать графы в различных жизненных ситуациях. Возникает вопрос, что же такое граф. Граф – это модель ситуации, в которой объекты моделирования обозначены точками, кругами, прямоугольниками, а связи между ними – линиями. Перед вами пример графа переливания крови.
На этой схеме объект моделирования – различные виды групп крови человека обозначены кругами – это вершины графа. А стрелками показано, какую кровь можно переливать человеку с данной группой крови. Стрелки называются дугами графа. Дуга, исходящая от вершины и направленная к этой же вершине, называется петлей. Данный граф отражает такую жизненную ситуацию как переливание крови.
При помощи графа можно решать различные запутанные задачи. Рассмотрим шуточную задачу «ХВОСТ БАРБОСА».
Собаки с рыжими хвостами
Себе овсянку варят сами.
Тем, чьи хвосты стального цвета,
Не позволяют делать это.
Кто варит сам себе овсянку,
Гулять выходит спозаранку.
Все, кто гулять выходят рано,
Не терпят фальши и обмана.
Вид добродушный у Барбоса,
Но на сорок он смотрит косо.
Он видит: норовят сороки
У воробьёв списать уроки!
Скажите – проще нет вопроса! –
Какого цвета хвост Барбоса?
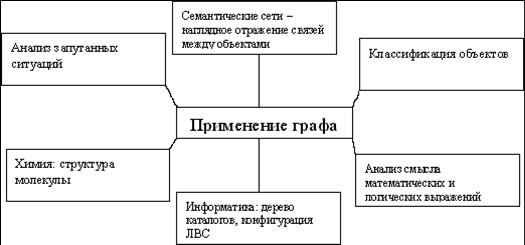
Такую запутанную ситуацию легко можно решить, смоделировав стихотворение в виде графа. А в каких ещё случаях используются графы? Исследовать этот вопрос вы будете самостоятельно, работая в группах. Каждая группа будет работать над одним направлением, выполняя предложенные задания. Результаты работы мы будем фиксировать в опорном конспекте, заполняя итоговую схему о применении графов. Одну вершину мы можем уже записать – анализ запутанных ситуаций. Названия остальных вершин вы будете заполнять в течение урока, когда спикеры групп будут докладывать результаты своей работы. Попутно я предлагаю вам подумать над таким вопросом: «Почему понятие графа изучается в школьном курсе информатики?» Ответить на который я вас попрошу в конце урока.
II. Работа по группам
1. Изучите предложенную теорию.
2. Выполните задание.
3. Оформите решение на пленке.
4. Спикер должен подготовить доклад о результатах работы по предложенному плану.
1 группа. Семантические сети.
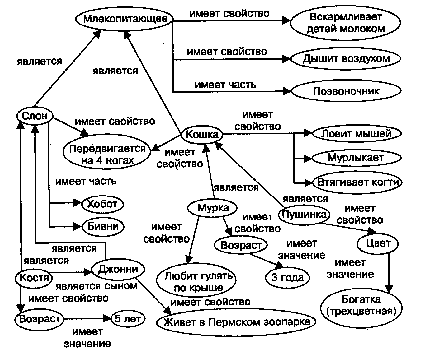
Семантическая сеть – модель знаний в форме графа. В основе таких моделей лежит идея о том, что любые знания можно представить в виде совокупности объектов (понятий) и связей (отношений) между ними. Рассмотрим пример семантической сети, представленной на рисунке.
Данный пример хорошо иллюстрирует отличие модели знаний от базы данных. Семантическая сеть наглядно отражает взаимосвязь входящих в нее объектов. Например, если в базу данных о животных добавить новую запись «Ник – это слон», то мы будем знать про Ника один только этот факт и все. Но если добавить этот факт в данную семантическую сеть, то сразу же станет ясно, что Ник – это млекопитающее, его детей надо вскармливать молоком, что он дышит воздухом, передвигается на четырех ногах, имеет хобот, бивни и позвоночник, принадлежит к тому же классу, что Джонни, Костя и пр.
В виде семантической сети можно представить различные системы. Например,
1. Система «Школьный урок», состоящая из следующих элементов: ученик, учитель, учебник, тетрадь, классный журнал, классная доска, мел, парта, учительский стол, классная комната.
2. Круговорот воды в природе.
3. Система высших органов власти Российской Федерации.
Задание. Представьте в виде семантической сети схему питания для системы, состоящей из следующих организмов: трава, кролики, волки, травоядные насекомые, воробьи, ястребы, жуки-навозники.
2 группа. Представление данных в форме дерева.
Особым видом графа является дерево. Данная форма модели применяется тогда, когда элементы моделируемого объекта находятся в состоянии какого-либо подчинения и соподчинения, когда есть отношение иерархичности.
Пример. Модель управления предприятием (школой, театральным коллективом и т. д.) очень удобно представлять в виде дерева.
Пример. Вам хорошо известно понятие «родословное дерево» и вы можете изобразить в такой форме ваши родственные отношения.
Пример. Каталог файлов на диске, также как и библиотечный каталог — примеры информационных моделей в форме дерева.
Формализация в случае построения дерева (иерархического графа) сводится к выявлению основного (главного, центрального) элемента рассматриваемого объекта (вершина нулевого уровня, которую часто называют корнем, элементов, которые находятся в непосредственном подчинении от основного (вершины 1-го уровня). Затем определяются вершины, находящиеся в непосредственном «подчинении» от вершин 1-го уровня (вершины 2-го уровня) и так далее.
Изображать построенное дерево отношений можно в любом направлении — это уже дело эстетического вкуса разработчика модели.
В научной и учебной деятельности с помощью деревьев часто представляют классификацию изучаемых объектов. Классифицирование — распределение объектов по классам в зависимости от их общих признаков, фиксирующее закономерные связи между классами объектов в единой системе данной отрасли знания. Пример.
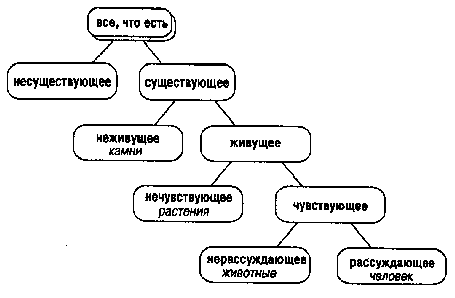
На рис. вы видите классификацию, предложенную Григорием Великим, которая призвана была показать, что человек имеет что-то общее со всеми видами существующих в мире вещей, и поэтому его справедливо называют «вселенной в миниатюре».
Задание. Известно, что древнерусский язык и общеславянский язык произошли от общеиндоевропейского языка. От древнерусского языка отошли русский, украинский и белорусский языки. От общеславянского языка отошли польский, чешский, болгарский и словенский языки.
Представьте предложенную информацию в виде графа.
3 группа. Смысл математических и логических выражений.
Традиционная математическая символика является формальным языком математики. В отличие от естественных языков, формальные языки не носят национального характера. Они придуманы для профессиональной деятельности людей и понятны специалистам всего мира.
Смысл математического выражения заключается в определяемой им последовательности вычислительных операций. Чтобы его понять, нужно знать правила старшинства операций, правила раскрытия скобок. Например, в выражении 7-5x3 в первую очередь следует выполнить действие, записанное вторым, что может показаться противоестественным. Если этого правила не знаешь, то ошибешься в вычислениях.
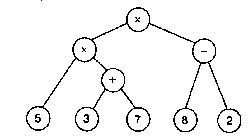
Наглядным средством изображения последовательности вычисления математических выражений, т.е. их смысла, являются графы. Такой граф представляет собой дерево, листьями которого являются числа, а прочими вершинами – операции. Ребра связывают вершину-операцию с вершинами операндами. Например для формулы 5x(3 + 7)x(8 - 2) дерево будет иметь такой вид.
Последовательность выполнения операций определяется при прохождении дерева от листьев к корю (снизу – вверх). Последней выполнится операция, отмеченная в корне (главной вершине, изображенной сверху). Аналогично с помощью графа может быть представлено и логическое выражение, в этом случае листьями будут являться логические переменные, а прочими вершинами – логические операции (конъюнкция, дизъюнкция, инверсия и т.д.)
Задание: Постройте дерево для следующего арифметического выражения. 6x4 + 7x(9 - 1)
III. Общее обсуждение разрешаемой проблемы
В ходе работы учитель помогает каждой группе выполнить задания. После выполнения задания спикер каждой группы докладывает результаты работы по приведенному плану. Остальные учащиеся во время доклада спикера заполняют граф. (См. рисунок ниже).
Вопросы:
На каких школьных предметах вы встречались с графами, приведите примеры (продолжаем заполнение графа)?
IV. Рефлексия
«Почему понятие графа изучается в школьном курсе информатики?»
Дополнительные вопросы:
• Нужно ли на уроках информатики знакомиться с понятием графа и учиться строить их?
• Как вы считаете, с какой целью было введено понятие графа в школьный курс информатики?
• Какие качества личности позволяет развить умение строить графы?
Попробуйте сделать вывод о значении информатики и графов в частности для остальных учебных предметов. Информатика дает инструмент для познания любой научной дисциплины.