Двоичная система счисления
| Строка 20: | Строка 20: | ||
Получим: | Получим: | ||
| − | [[Изображение:2СС.jpg]] | + | [[Изображение: 2СС.jpg]] |
Если старшая триада не заполнена до конца, следует дописать в ее старшие разряды нули. После этого необходимо заменить двоичные триады , начиная с младшей, на числа, равные им в восьмеричной системе, получим следующее: | Если старшая триада не заполнена до конца, следует дописать в ее старшие разряды нули. После этого необходимо заменить двоичные триады , начиная с младшей, на числа, равные им в восьмеричной системе, получим следующее: | ||
| − | [[Изображение:2cc1.jpg]] | + | [[Изображение: 2cc1.jpg]] |
Таким образом, | Таким образом, | ||
| − | [[Изображение:2cc2.jpg]] | + | [[Изображение: 2cc2.jpg]] |
'''Из двоичной в шестнадцатеричную:''' | '''Из двоичной в шестнадцатеричную:''' | ||
| Строка 31: | Строка 31: | ||
При переводе чисел из двоичной системы счисления в шестнадцатеричную поступаем таким же образом, но разбиение двоичного числа производим на тетрады (по 4 символа). Для примера будем использовать следующее двоичное число: 100010011110 | При переводе чисел из двоичной системы счисления в шестнадцатеричную поступаем таким же образом, но разбиение двоичного числа производим на тетрады (по 4 символа). Для примера будем использовать следующее двоичное число: 100010011110 | ||
Разбиваем двоичное числа на тетрады: | Разбиваем двоичное числа на тетрады: | ||
| − | [[Изображение:16cc.jpg]] | + | [[Изображение: 16cc.jpg]] |
Заменяя двоичные тетрады на их шестнадцатеричные значения, получим искомое шестнадцатеричное число: | Заменяя двоичные тетрады на их шестнадцатеричные значения, получим искомое шестнадцатеричное число: | ||
| − | [[Изображение:16cc1.jpg]] | + | [[Изображение: 16cc1.jpg]] |
| Строка 39: | Строка 39: | ||
Чтобы перевести число из двоичной системы счисления в десятичную надо для начала расставить степени чисел справа налево, затем в том же порядке нужно умножить числа на 2( т.к. двоичная система счисления), при это возведя двойку в степень указанную над числом, например: | Чтобы перевести число из двоичной системы счисления в десятичную надо для начала расставить степени чисел справа налево, затем в том же порядке нужно умножить числа на 2( т.к. двоичная система счисления), при это возведя двойку в степень указанную над числом, например: | ||
| − | [[Изображение:10cc.jpg]] | + | [[Изображение: 10cc.jpg]] |
Также, кому интересно, прошу посетить некоторые видеоуроки по переводам: | Также, кому интересно, прошу посетить некоторые видеоуроки по переводам: | ||
| + | |||
[http://rutube.ru/tracks/4108693.html Перевод из десятичной СС в двоичную и обратно] | [http://rutube.ru/tracks/4108693.html Перевод из десятичной СС в двоичную и обратно] | ||
| + | |||
[http://www.youtube.com/watch?v=vQ748FuizOM&feature=related Сложение чисел в двоичной системе счисления] | [http://www.youtube.com/watch?v=vQ748FuizOM&feature=related Сложение чисел в двоичной системе счисления] | ||
Версия 19:28, 13 сентября 2011
Автор-составитель: Асфандияров Валентин
Двоичная система счисления — это позиционная система счисления с основанием 2. В этой системе счисления числа записываются с помощью двух символов (0 и 1).
История
- Индийский математик Пингала (200 год до н. э.) разработал математические основы для описания поэзии с использованием первого известного применения двоичной системы счисления.
- Наборы, представляющие собой комбинации двоичных цифр, использовались африканцами в традиционных гаданиях (таких как Ифа) наряду со средневековой геомантией.
- В 1605 году Френсис Бэкон описал систему, буквы алфавита которой могут быть сведены к последовательностям двоичных цифр, которые в свою очередь могут быть закодированы как едва заметные изменения шрифта в любых случайных текстах. Важным шагом в становлении общей теории двоичного кодирования является замечание о том, что указанный метод может быть использован применительно к любым объектам.
Правила перевода.
Из двоичной в восьмиричную:
Пусть требуется перевести двоичное число 110001001 в восьмеричную систему счисления. Для этого следует разбить это двоичное число на триады (по 3 символа) , начиная с младшего бита. Получим:
Если старшая триада не заполнена до конца, следует дописать в ее старшие разряды нули. После этого необходимо заменить двоичные триады , начиная с младшей, на числа, равные им в восьмеричной системе, получим следующее:
Таким образом,
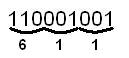
Из двоичной в шестнадцатеричную:
При переводе чисел из двоичной системы счисления в шестнадцатеричную поступаем таким же образом, но разбиение двоичного числа производим на тетрады (по 4 символа). Для примера будем использовать следующее двоичное число: 100010011110
Разбиваем двоичное числа на тетрады:
Заменяя двоичные тетрады на их шестнадцатеричные значения, получим искомое шестнадцатеричное число:
Из двоичной в десятичную:
Чтобы перевести число из двоичной системы счисления в десятичную надо для начала расставить степени чисел справа налево, затем в том же порядке нужно умножить числа на 2( т.к. двоичная система счисления), при это возведя двойку в степень указанную над числом, например:
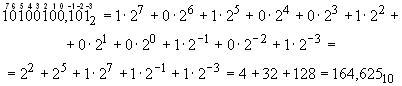
Также, кому интересно, прошу посетить некоторые видеоуроки по переводам:
Перевод из десятичной СС в двоичную и обратно
Сложение чисел в двоичной системе счисления
Допольнительно:
Пройдите, пожалуйста, не большой тест по двоичной системе счисления.
Источники информации:
3.Основные определения и положения микропроцессорной техники
