Система остаточных классов
| Строка 1: | Строка 1: | ||
| − | Представление числа в системе остаточных классов основано на понятии вычета и китайской теореме об остатках. СОК определяется набором взаимно простых модулей | + | Представление числа в системе остаточных классов основано на понятии вычета и китайской теореме об остатках. СОК определяется набором взаимно простых модулей [[Изображение:1.png]] с произведением [[Изображение:2.png]] так, что каждому целому числу x из отрезка [0,M − 1] ставится в соответствие набор вычетов [[Изображение:3.png]]При этом китайская теорема об остатках гарантирует однозначность представления для чисел из отрезка [0,M − 1]. |
| − | При этом китайская теорема об остатках гарантирует однозначность представления для чисел из отрезка [0,M − 1]. | + | |
В СОК арифметические операции (сложение, вычитание, умножение, деление) выполняются покомпонентно, если про результат известно, что он является целочисленным и также лежит в [0,M − 1]. | В СОК арифметические операции (сложение, вычитание, умножение, деление) выполняются покомпонентно, если про результат известно, что он является целочисленным и также лежит в [0,M − 1]. | ||
Недостатками СОК является возможность представления только ограниченного количества чисел, а также отсутствие эффективных алгоритмов для сравнения чисел, представленых в СОК. Сравнение обычно осуществляется через перевод аргументов из СОК в смешанную систему счисления по основани | Недостатками СОК является возможность представления только ограниченного количества чисел, а также отсутствие эффективных алгоритмов для сравнения чисел, представленых в СОК. Сравнение обычно осуществляется через перевод аргументов из СОК в смешанную систему счисления по основани | ||
| − | |||
Версия 10:55, 28 сентября 2011
Представление числа в системе остаточных классов основано на понятии вычета и китайской теореме об остатках. СОК определяется набором взаимно простых модулей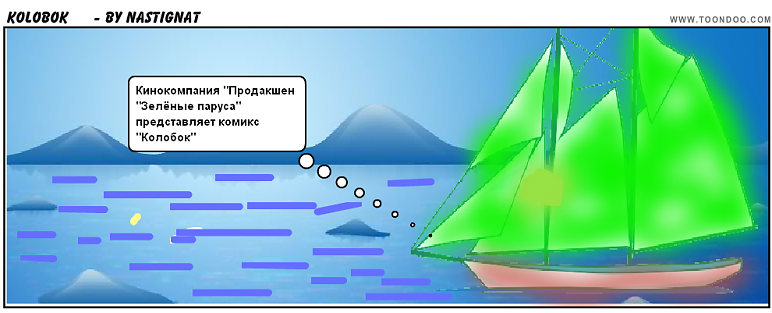 
с произведением 
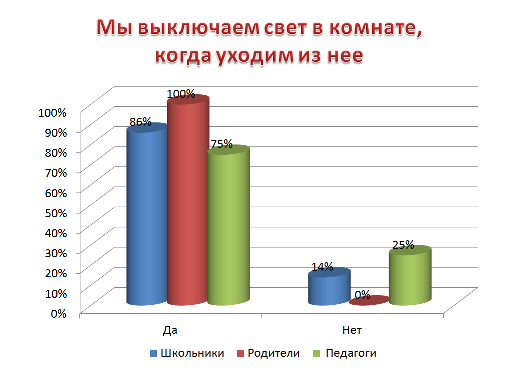так, что каждому целому числу x из отрезка [0,M − 1] ставится в соответствие набор вычетов 
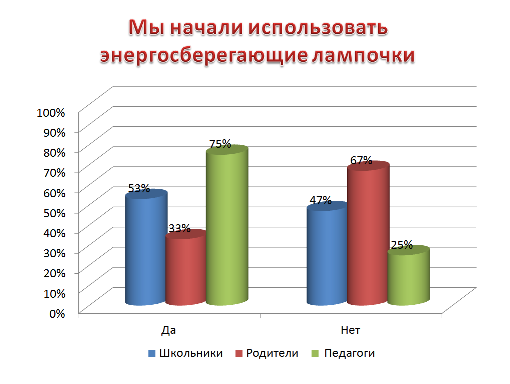При этом китайская теорема об остатках гарантирует однозначность представления для чисел из отрезка [0,M − 1].
В СОК арифметические операции (сложение, вычитание, умножение, деление) выполняются покомпонентно, если про результат известно, что он является целочисленным и также лежит в [0,M − 1].
Недостатками СОК является возможность представления только ограниченного количества чисел, а также отсутствие эффективных алгоритмов для сравнения чисел, представленых в СОК. Сравнение обычно осуществляется через перевод аргументов из СОК в смешанную систему счисления по основани
