Копилка знаменитых задач продолжение 6

Материал из ТолВИКИ

(Различия между версиями)

Версия 22:44, 9 ноября 2008

Посмотреть страницу Копилка знаменитых задач.

Задачи участников ДООМ

--Bookworm ID 213 13:03, 4 ноября 2008 (UZT)

Задача № 39. Старинная задача: Один пастух говорит другому: «Дай мне одну из твоих овец и у меня буде вдвое более овец чем у тебя». Второй пастух отвечает: Нет, лучше ты дай мне одну из твоих овец, тогда у нас будет овец поровну». Сколько овец было у каждого пастуха? Решение: Обозначим кол-во овец первого пастуха за х, а кол-во овец у второго – у. Тогда получим систему из двух уравнений: х+1=(у-1)2 и х-1=у+1. Решая систему получим, что х=7, а у=5. Ответ: у первого пастуха было 7 овец, а у второго 5. Задача № 40. Задача Льюиса Кэррола. Несколько человек сидят по кругу так, что у каждого из них имеется по одному соседу справа и слева. Каждый из сидящих располагает определенным количеством шиллингов. У первого на 1 шиллинг больше, чем у второго, у второго на 1 шиллинг больше, чем у третьего, и т. д. Первый из сидящих отдает 1 шиллинг второму, второй 2 шиллинга третьему и т. д. Каждый отдает следующему на 1 шиллинг больше, чем получил сам, до тех пор, пока, это возможно. В результате у одного из сидящих шиллингов оказывается в 4раза больше, чем у его соседа. Сколько всего было людей и сколько шиллингов было сначала у самого бедного из них? Решение: Пусть m–число людей, k–число шиллингов у последнего (самого бедного) из них. После первого тура каждый из участников игры станет на 1 шиллинг беднее, а сумма, передаваемая последним из игроков первому, составит m шиллингов. Следовательно, после некоторого числа k туров каждый участник станет беднее на k шиллингов, у последнего участника не останется ни одного шиллинга, а сумма передаваемая им первому участнику, составит mk шиллингов. Игра прекратится на следующем туре, когда очередь пополнять «передвижную кассу» дойдет до последнего игрока. В это момент в «кассе» будет mk+m–1 шиллингов, у предпоследнего игрока не останется ничего, а у первого m–2 шиллингов. Ясно, что единственными участниками, «состояния» которых относятся как 4:1, могут быть лишь первый и последний игроки. Следовательно, mk+m–1=4(m–2), либо 4(mk+m–1)=m–2. Первое уравнение преобразуем к виду mk=3m–7, или k=3–7/m. Ясно, что оно не имеет иных решений в целых числах, кроме m=7, k=2. Второе уравнение преобразуется к виду 4mk=2–3m. Оно не имеет решений в целых положительных числах. Ответ: 7 человек, 2 шиллинга.

Задача №41. Задача Льюиса Кэррола. 1 июля, когда на моих карманных часах было 8 часов утра, стенные часы показывали 8часов 4 минуты. Взяв с собой карманные часы, я отправился в Гринвич и обнаружил, что, когда они показывают полдень, точное время в действительности равно 12часам 5 минутам. Вечером того же дня, когда на моих часах было ровно 6 часов, стенные часы показывали 5часов 59 минут. 30 июля в 9 часов утра по моим карманным часам стенные часы показывали 8часов 59 минут. В Гринвиче, когда мои карманные часы показывали 12 часов 10 минут, точное время было 12часов 5 минут. Вечером того же дня карманные часы уже показывали 7 часов, когда на стенных ещё было 6 часов 58 минут. Карманные часы я завожу лишь при поездке в Гринвич. В течении суток они идут равномерно. Настенные часы идут всегда, причем идут равномерно. Каким образом мне узнать, когда наступает полдень (по точному времени) 31 июля? Решение: 1 июля мои карманные часы за 10 ч ушли вперед по сравнению со стенными часами на 5 мин, то есть спешили на ½ мин в час, или на 2 мин в 4 часа. Следовательно, когда карманные часы показывали полдень, на стенных часах было 12ч 2 мин. Иначе говоря, в тот момент, когда точное время было 12ч 5мин, стенные часы отставали на 3мин (от точного времени). 30 июля карманные часы отстали от стенных на 1мин за 10ч, то есть отставали на 6с в час, или на 19с за 3ч 10мин. Таким образом, когда карманные часы показывали 12ч 10мин, на стенных было 12ч 7мин 19с. иначе говоря, в момент, когда точное время было 12ч 5мин, стенные часы спешили на 2мин 19с (по сравнению с точным временем). Итак, стенные часы уходят вперед по сравнению с точным временем на 5мин 19с за 29дней, что составляет 319с за 29дней, или 11с в день, или 11/24*12с за 5мин. Следовательно, 5 мин точного времени соответствует 5мин 11/288с, отсчитанным по карманным часам. 31 июля, когда точное время равнялось 12ч 5мин, стенные часы ушли вперед на 2мин 19с+11с, то есть показывали 12ч 7½мин. Следовательно, если вернуться на 5мин назад по точному времени, то стрелки стенных часов следует отвести на 5мин 11/288с назад, то есть поставить так, чтобы они показывали12ч 2мин 29 277/288с. Ответ: в момент, когда 31 июля стенные часы показывают это время, по точному времени наступает полдень.

Задача №42. Задача Льюиса Кэррола. Два пешехода А и В пускаются в путь ровно в 6 часов утра в один и тот же день. Оба идут по одной дороге и в одном направлении. Пешеход В сначала опережает пешехода А на 14 миль. Оба идут с 6 утра до 6 вечера. В первый день пешеход А, двигаясь с постоянной в течении дня скоростью, проходит 10 миль, во второй - 9, в третий – 8 миль и т. д. Пешеход В, двигаясь также с постоянной в течении дня скоростью, проходит в первый день 2 мили, во второй – 4, в третий 6 и т. д. Где и когда пешеход А нагонит Пешехода В? Решение: Пусть х - число дней, прошедших с того момента, как пешеходы пустились в путь, до встречи. Тогда: [2*10–([х–1)]*х/2=14+[2*2+( х–1)*2]*х/2 То есть: 21х/2 – х2/х=14+х+х2 3х2–19х+28=0 х1=4, х2=7/3. Ответ 7/3 указывает на то, что встреча происходит на 3-й день. Ведем у – число часов, которое пешеходы находятся в пути. Отсчитывается с 6-ти часов утра каждого дня. К концу второго дня пути А пройдет 19 миль, а В будет находиться от пункта отправления А на расстоянии 14+6=20 миль. Следовательно, 19 + у*8/12=20+у*6/12 у*2/3=1+у*1/2 откуда у= 6. Таким образом, пешеходы встречаются по происшествии двух с половиной дней (2 дня 6 ч) и четырех дней пути на расстояниях в 23 и 34 мили от отправного пункта пешехода А.

Задача №43. Задача Льюиса Кэррола. Пятеро друзей решили на паях организовать компанию по торговле вином. Каждый из них внес в фонд компании одинаковое количество бутылок, купленного по одной цене. Один из друзей на общем собрании «акционеров» был избран казначеем, другой - продавцом. В обязанность продавцу вменялось продавать вино с 10%-ной надбавкой (по сравнению с покупной ценой). В первый день продавец распил одну бутылку вина, несколько бутылок продал, а всю выручку передал казначею. На второй день продавец не стал пить вина, но прикарманил деньги, полученные от продажи одной бутылки, а всю остальную выручку передал казначею. Вечером того же дня казначей наведался в погреба фирмы и пересчитал оставшиеся бутылки. «вина ровно на 11 фунтов стерлингов», - заметил он себе под нос, покидая погреб. На третий день продавец выпил одну бутылку вина, присвоил себе деньги, полученные от продажи другой бутылки, а всю остальную выручку передал казначею. Поскольку все вино было продано, друзья созвали общее собрание «акционеров» и к своему огорчению обнаружили, что их доходы (то есть разность между суммами, переданными продавцом казначею , и первоначальной стоимостью вина) составили лишь 6 пенсов за бутылку. Доходы эти поступали в течении трех дней равномерно (то есть разность между выручкой, переданной продавцом казначею в конце каждого дня, и первоначальной стоимостью проданного за день вина была одной и той же в течение всех трех дней), но об этом, разумеется, знал лишь продавец. 1. Сколько бутылок вина было куплено в фонд компании? 2. По какой цене друзья покупали вино? Решение: Обозначим число бутылок вина, проданных в первый, второй и третий день, через х, у, z. Предположим, что каждая бутылка была куплена за 10v пенсов и, следовательно, продана за 11v пенсов. В первый день казначей получил от продавца (х–1 )*11v, во второй у*11v –v и в третий день (z –1) *11v–v пенсов. Следовательно, прибыль (разность между выручкой и затратами на покупку вина) составила: в первый день хv–11 , во второй день уv–v и в третий zv-12v пенсов. По условию задачи все три величины равны, откуда у=х–10, z=х+1. Таким образом, полное число бутылок (х+у+z), хранившихся в начале в винном погребе «фирмы», равно 3х – 9. Прибыль от продажи всех бутылок составила (х+у+z)v–24v=(3х–33)v, а прибыль от продажи одной бутылки равна [(3х–33)v]/3х–9.(По условию задачи эта величина равна 6 пенсам.) (х–11)v=(х–3)6 Кроме того, z*11v=11*240, то есть (х+1)*11v=11*240. Комбинируя эти два уравнения, получаем: (х–11)/х+1=6(х–3)/240 (х+1)(х–3)=40(х–11) х2–2х–3=40х–440 х2–42х+437=0 х1,2=(42±4)/2, х1=23, х2=19. Итак, число бутылок равно либо60, либо 48, но поскольку оно должно быть кратно 5, остается лишь одно решение: 60 бутылок. Поскольку(х+1)*11v=11*240, или 24v= 240, то v=10. таким образом, вино было куплено по цене 8 шиллингов 4 пенса за бутылку и продано по цене 9 шиллингов 2 пенса за бутылку. Ответ: Было куплено 60 бутылок, по цене 8 шиллингов 4 пенса за бутылку. --Bookworm ID 213 13:03, 4 ноября 2008 (UZT)

Задачи команды ЛАДА-ВЕКТОР ID_279

Задача №15

Задача из папируса Ахмеса, Египет, ок. 2000г. до н.э.

Приходит пастух с 70 быками. Его спрашивают : «Сколько приводишь ты из своего многочисленного стада?» Пастух отвечает «Я привожу две трети от трети скота. Сочти. Сколько быков в стаде?

Решение: 70быков – 2/3 от трети скота

70:2/3=105(быков) – треть скота

105:1/3=315(быков)

Ответ: В стаде 315 быков.

Задача №16

Задача Евклида, Греция

Ослица и мул шли вместе, нагруженные мешками равного веса. Ослица жаловалась на тяжесть ноши.«Чего ты жалуешься? -сказал мул. Если ты дашь мне один свой мешок моя ноша станет вдвое больше твоей, а если я дам тебе один мешок наши грузы сравняются». Сколько мешков было у каждого?

Решение:

Обозначим за Х число мешков у каждого после передачи одного мешка от мула к ослице. Тогда первоначально у мула было (Х+1) мешков , а у ослицы (Х-2) в два раза меньше, чем у мула.

Составим и решим уравнение:

х+2=2(х-2)

х+2=2х-4

х=6

6+1=7(мешков)- у мула

6-1=5(мешков)- у ослицы

Ответ: 5мешков у ослицы и 7мешков у мула.

Задача №17

Старинная задача

На вопрос о возрасте одна дама ответила: «Мой возраст таков ,что если его возвести в квадрат или умножить на 53 и из результата вычесть 696 ,то получится одно и тоже».

Решая квадратное уравнение, автор замечает: «Так как вопрос касается возраста дамы, то из вежливости нужно перед радикалом поставить нижний знак».

Решим эту задачу с этим дополнительным условием.

Пусть даме x лет. Составим уравнение:

x = 53x – 696,и решим его беря (из вежливости) перед радикалом нижний знак.

x – 53x + 696 = 0

Д = 53 – 4 × 696 = 2809 - 2784 =25, квдратный корень из 25 = 5.

Получим x = (53- 5)/2=24. Итак, даме было 24 года.

Задача № 18

Задача Ал – Каши

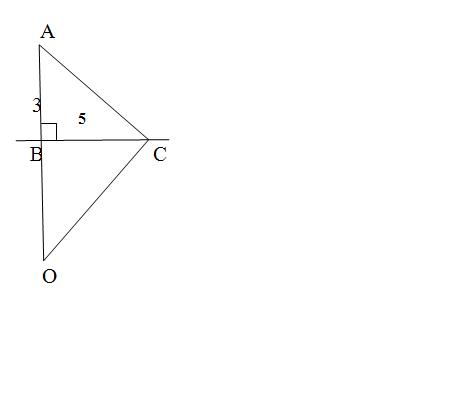
Копьё стояло в воде отвесно и высовывалось наружу на 3 локтя. Порыв ветра наклонил его , причём нижний конец копья не изменил положение ,а верхний оказался на поверхности воды на расстоянии 5 локтей от того места где раньше копьё высовывалось из воды. Мы хотим узнать длину копья.

Решение:

Сделаем рисунок.

Введём обозначения.

АО перпендикулярно ВС,

АВ = 3 локтя,ВС = 5локтей

Найдём АО.

АО = АВ + ВО

Найдём ВО.

Рассмотрим прямоугольные подобные треугольники АВС и ВСО.

Из подобия треугольника АВС и треугольники ВСО:

АВ/ВС= ВО

3/5=5/ВО

Во = 25/3=8 1/3

АО=АВ=ВО=3+8 1/3=11 1/3 (локтя)

Ответ: Длина копья 11 1/3 локтя.

Задача №19

Задача древнего Китая

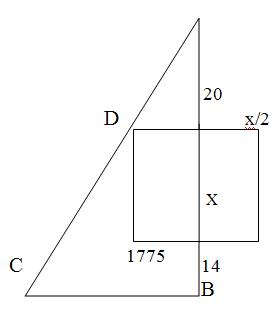
Город имеет форму квадрата, в середине каждой стороны которого имеются ворота. Вне города, на расстоянии 20 бу север от северных ворот, стоит столб. Если пройти от южных ворот 14 бу на юг, а затем повернуть на запад и пройти ещё 1775 бу, то как раз в этот момент из-за стен города покажется столб. Какова ширина города?

Задача № 20

Задача (Из арифметики Л.Ф. Магницкого.)

У некоторого человека были для продажи вина двух сортов. Первое ценною 10 гривен ведро, второе же – по 6 гривен. Захотелось ему сделать из тех двух вин, взяв по части, третье вино, чтобы ему цена была по 7 гривен. Какие части надлежат из тех двух вин взять к наполнению ведра третьего вина ценою 6 гривен.

Современное решение:

Пусть для составления одного ведра требуемой смеси нужно взять х ведер первого сорта (х 1) и (1-х) ведер второго сорта. первая часть вина стоит 10х гривен, а вторая 6(1-х) гривен.

Составим уравнение:

10х+6(1-х) = 7, откуда х =1/4 , 1 – х = 3/4 .

Итак, нужно взять 1/4 ведра вина по 10 гривен и 3/4 ведра вина по 6 гривен за ведро.

Старинный способ решения:

Запишем цены вин каждого сорта и цену смеси так:

Вычислить прибыль 7-6=1 и убыток 10-7=3 на каждом ведре и запишем результат по линиям:

Таким образом, 3 части из четырёх приходятся на более дешевое вино и 1 часть – на более дорогое.

--Лада-Вектор ID 279 22:30, 4 ноября 2008 (UZT)

Задача № 21

Задачи из «Арифметики» Л.Ф.Магницкого.

Собака и заяц. Собака усмотрела зайца в 150 саженей от себя. Заяц пробегает за 2 минуты 500 саженей, а собака- за 5 минут 1300 саженей. За какое время собака догонит зайца? Решение: За одну минуту заяц пробегает 250 саженей, а собака 260 саженей. Следовательно, за одну минуту расстояние между собакой и зайцем уменьшиться на 10 саженей. Поскольку между собакой и зайцем, когда собака увидала зайца, было 150 саженей, то собака догонит зайца через 150 х 10= 15 минут.

Задача №22

Задачи из «Арифметики» Л.Ф.Магницкого.

Два воина.

Один воин вышел из города и проходил по 12 верст в день, а другой вышел одновременно и шел так: в первый день прошел 1 версту, во второй день 2 версты, в третий день 3 версты, в четвертый день 4 версты, в пятый 5 верст и так прибавлял каждый день по одной версте, пока не настиг первого. Через сколько дней в второй воин настигнет первого? Решение: В первый день второй воин отстанет на 12 – 2 = 11 верст, во второй еще на 12 – 2 = 10 верст, в третий еще на 12- 3 =9 верст и так далее. На 12 ый день отставание составит (11 +10+9+…+2+1+0) верст. А затем расстояние между ними начнет сокращаться. В 13- й день на 13 – 12 = 1 версту, в 14 день еще на 14 – 12 = 2 версты, в 15 –й день еще на 15 – 12 =3 версты, и , наконец , в 23-й день на 23 – 12= 11 верст. На 23-й день расстояние между ними уменьшиться на ( 1+2+3+…+10+11) верст. Это значит, что второй воин по прошествии 23 дней догонит первого.

Задача №23

Задача XVIII века.

«С чем иностранка к россам привезена?»

Нововыезжей в Россию иностанной мадаме

Вздумалось оценить свое богатство в чемодане:

Новой выдумки нарядное фуро

И праздничный чепец а ля фигаро.

Оценщик был русак,

Сказал мадаме так:

«Богатство твоего первая вещь фуро

Вполчетверта дороже чепца фигаро;

Вообще же не с половиной четыре алтына,

Но настоящая им цена только сего половина»

Спрашивается каждой вещи цена,

С чем иностранка к россам привезена?

(« Вполчетверта»- в 3 1/2 раза).

Решение:

Все имущество мадам было оценено в 1/2 х (4 +1/2) алтынов, что составляет 27/4 копеек. « Чепец фигаро» по условию в 3 1/2 раза дешевле «фуро», и, следовательно , в 4 1/2=9/2 раза дешевле всего имущества. Поэтому чепец стоит 27/4 : 9/2 = 3/2 копейки, а стоимость «фуро» равна 3/2х 31/2=21/4 копейки

Задача №24

Задача XVIII века.

Три бочки.

Хозяин имеет три бочки А,В и С. Бочка А наполнена квасом, бочки В и С- пустые. Если квасом из бочки А наполнить бочку В, то в бочке А останется 2/5 ее содержимого .Если же квасом из бочки А наполнить бочку С, то в бочке А останется 5/9 ее содержимого. Чтобы наполнить обе бочки В и С, надо взять содержимое бочки А и еще добавить 4 ведра кваса. Сколько ведер кваса вмещает каждая бочка?

Решение

Так как после наполнения бочки В в бочке А остается 2/5 ее содержимого, то вместимость бочки В равна3/5 вместимости А. Так как после наполнения бочки С в бочке А остается 5/9ее содержимого, то вместимость бочки С равна 4/9 вместимости бочки А.Значит , вместимость бочек. В и С равна – 3/5+4/9= 47/45=1+ 2/45 вместимости бочки А. Из условия задачи тогда следует, что 2/45 Вместимости бочки А составляют 4 ведра , откуда получаем , что вместимость бочки В равна 90 х 4/9= 40 ведер.

--Лада-Вектор ID 279 23:30, 5 ноября 2008 (UZT)

--Bookworm ID 213 14:15, 5 ноября 2008 (UZT) Задача № 44:Задача из акмимского папируса. Некто взял из сокровищницы 1/13. Из того, что осталось, другой взял 1/17, оставив же он в сокровищнице 150. Сколько было в сокровищнице первоначально? Решение: В рукописи дробная часть ответа 17221/32 дается в виде суммы дробей, числители которых равны 1, а именно: 1/2 + 1/8 + 1/48 + 1/96. Ответ: В сокровищнице было 17221/32.

Задача № 45:Задача Диофанта (из трактата «Арифметика»). Требуется число 100 разделить два раза так, чтобы большая его часть от первого деления была вдвое более меньшей части от второго деления и чтобы большая часть от второго деления Решение: Обозначим меньшую часть от второго деления через х, тогда большая часть от первого деления будет 2х. Найдем теперь меньшую часть от первого деления. Она будет равна 100 – 2х. Следовательно, большая часть второго деления равняется 300 – 6х. Ясно, что обе части от второго деления должны составить 100, т. е. х+(300 – 6х) = 100, откуда х = 40. Следовательно, результат первого деления: меньшая часть равна 20, большая – 80. Результат второго деления: меньшая часть равна 40, большая часть – 60. Ответ: Результат первого деления: меньшая часть равна 20, большая – 80; результат второго деления: меньшая часть равна 40, большая часть – 60.

Задача № 46: Задача из греческой антологии. Видя, что плачет Эрот, Киприда его вопрошает: «Что так тебя горчило, ответствуй немедля!» «Яблок я нес с Геликона немало, - Эрот отвечает, - Музы, отколь ни возьмись, напали на сладкую ношу Частью двенадцатой вмиг овладела Евтерпа, а Клио Пятою долю взяла. Талия – долю восьмую. С частью двадцатой ушла Мельпомена. Четверть взяла Терпсихора, С частью седьмой Эрато от меня убежала. Тридцать плодов утащила Полимния. Сотня и двадцать Взяты Уранией; триста плодов унесла Каллиопа. Я возвращаюсь домой почти что с пустыми руками, Только полсотни плодов мне оставили музы на долю». Решение: Пусть «Яблоки Эрота» - х, тогда осталось у него х – (1/12 х + 1/5 х + 1/8 х + 1/20 х + 1/4 х + 1/7 х) = 30 + 120 + 50. Решая уравнение получаем 25/168 х = 200, из этого х = 1344 яблока. Ответ: У Эрота было 1344 яблока.

Задача №47: Задача из греческой антологии. Вот Полифема циклопа из меди статуя отлита. Руку, уста и единое око ваятель сделал на диво, Скрывши в них трубы: водой великан истекает как будто. Хитрое в трубах устройство: ведущая в руку способна Весь водоем до краёв через три дня наполнить. Оку – достаточно дня, а устам и всего лишь две пятых, Вместе все три водоём скоро ли могут наполнить? Решение: Пусть водоем – 1, тогда скорости: руки – 3, ока – 1, уст – 2/5 . Получаем уравнение: 1: (3 + 1 + 2/5) = 4 2/5 дня. Ответ: За 4 2/5 дня рука, око и уста заполнят водоем.

Задача №48: Задача из греческой антологии.- Хроноса (бог времени) вестник, скажи, какая часть дня миновала? - Дважды две трети того, что прошло, остаётся. (У древних греков день длился 12 часов.) Решение: Задача сводится к решению уравнения 4/3 х + х = 12, откуда х = 5 1/7 дня. Ответ: 5 1/7 дня миновала. --Bookworm ID 213 14:15, 5 ноября 2008 (UZT)

Участник:ПОБЕДА ID_235

1. Четверо братьев

ЗАДАЧА

У четырех братьев 45 рублей. Если деньги первого увеличить на 2 рубля, деньги второго уменьшить на 2 рубля, деньги третьего увеличить вдвое, а деньги четвертого уменьшить вдвое, то у всех окажется поровну. Сколько было у каждого?

РЕШЕНИЕ

Пусть x руб. - у первого брата, y руб. - у второго брата, z руб. - у третьего брата, t руб. - у четвертого брата.

Составим уравнение:

x + 2 = y - 2 = 2z = t/2

Расчленяем уравнение на три отделоных и решаем.

x + 2 = y - 2

x + 2 = 2z

x + 2 = t/2. Получаем следующие ответы: x = 8, y = 12, z = 5, t = 20.

У первого брата 8 руб., у второго - 12 руб., у третьего - 5 руб., у четвертого - 20 руб.

2. Задача Д.И.Менделеева

Великий русский ученый Д.И.Менделеев, будучи директором Главной палаты мер и весов, интересовался задачей на взвешивание при помощи одного набора гирь. Задача заключаласб в следующем: "Если иметь набор гирь по одной каждого вида, например a, b, c, d г., то по скольку граммов должны быть эти гири, чтобы при помощи их можно было взвесить любой груз, не превышающий a + b + c + d граммов.

ЗАДАЧА

Пусть имеется любой груз в 86 г. Какие нужно выбрать гири, чтобы, имея только один набор их, уравновесить это груз, если положить гири только на правую чашку весов?

РЕШЕНИЕ

Так как всякое натуральное число можно выразить в двоичной чистеме счисления, где в каждом разряде может быть не более одной единицы, то получается, что всякое натуральное число может быть представлено в виде суммы степеней 2 и 1. На этом свойстве и основывается возможность на весах всякий груз, содержащий целое число граммов, гирями "двоичной системы счисления". Число 86 в двоичной будет 1010110 = 2⁶ + 2⁴ + 2² + 2 = 64 + 16 + 4 + 2. Имея набор гирь, груз 86 г может быть уравновешен гирями 64 г, 16 г, 4 г, 2 г.

3. Вечеринка

ЗАДАЧА

На вечеринке было 20 танцующих. Мария танцевала с семью танцорами, Ольга - с восемью, Вера - с девятью и так далее до Нины,Ю которая танцевала со всеми танцорами. Сколько танцоров (мужчин) было на вечеринке?

РЕШЕНИЕ

Будем искать число не танцоров, о танцорок, которое обозначим за x:

1-я, Мария, танцевала с 6 + 1 танцорами

2-я, Ольга,танцевала с 6 + 2 танцорами

3-я, Вера, танцевала с 6 + 3 танцорами

........................................

x-я, Нина, танцевала с 6 + x танцорами

Имеем уравнение

x + (6 + x) = 20

Откуда

x = 7,

Найдем количество танцоров:

20 - 7 = 13

7 танцоров было на вечеринке.

4. Мнимая нелепость

ЗАДАЧА

Чему равно 84, если 8*8=54?

РЕШЕНИЕ

Пусть основание неизвестной чистемы счисления - x. Число "84" означает тогда 8 единиц второго разряда и 4 единицы первого, т.е. "84" = 8x + 4.

Число "54" означает 5x + 4. Имеем уравнение 8*8=5x + 4, т.е. в десятичной системе 64 = 5x + 4, откуда x = 12. Числа написаны по двенадцатеричной системе, и "84" = 8*12 + 4 = 100. Значаит, если 8*8="54", то "84" =100.ъ

5. Утопить или повесть

ЗАДАЧА

Некто совершил преступление, караемая смертной казнью. На суде ему предоставляется последнее слово. Он должен произнести одно утверждение. Если оно окажется истинным - преступника утопят, если же оно окажется ложным, то преступника повесят. Какое утверждение он должен высказать, чтобы привести палачей в полное замешательство?

ОТВЕТ: Я буду повешен.

6. Парадокс цирюльника

ЗАДАЧА

В небольшом городке цирюльник бреет всех, кто не бреется сам и не бреет никого из тех, кто бреется сам. Бреет ли цирюльник самого себя? Если он бреет самого себя, то тем самым он нарушает правила, так как бреет одного из тех, кто бреется сам. Если же цирюльник не бреет самого себя, то он опять-таки нарушает правила, так как не бреет одного из тех, кто не бреется сам. Что делать цирюльнику?

ОТВЕТ: существование такого цирюльника логически невозможно.

7. Индусская задача(перевод Лебедева В.И., Автора книги "Кто изобрел алгебру?")

ЗАДАЧА

На две партии разбившись,

Забавлялись обезьяны.

Часть восьмая их в квадрате

В роще весело резвилась;

Криком радостным двенадцать

Воздух свежий оглашали.

Вместе сколько, ты мне скажешь,

Обезьян там было в роще?

РЕШЕНИЕ

Если общая численность стаи x, то

(x/8)² + 12 = x

откуда

x₁ = 48, x₂ = 16.

ОТВЕТ

Задача имеет два положительных решения: в стае могло быть или 48 обезьян, или 16. Оба ответа вполне удовлетворяют задаче.

--Bookworm ID 213 15:30, 6 ноября 2008 (UZT) Задача 49. Магницкого Л.Ф. Путешественники.Путешественник идет из одного города в другой 10 дней, а второй путешественник тот же путь проходит за 15 дней. Через сколько дней путешественники встретятся, если выйдут одновременно навстречу друг другу из этих городов? Решение. За тридцать дней путешественники проходят 30: 10 + 30: 15 = 5 расстояний между городами. Значит, они сойдутся через 30:5 = 6 дней.

Задача 50. Магницкого Л.Ф. Вокруг города. Два человека пошли одновременно друг за другом из одного места вокруг города. Один из них идет по 4 версты в час, а второй по 3 целых 1/3 версты в час. Путь вокруг того же города составляет 15 верст. Через сколько часов они сошлись и сколько раз каждый из них обошел город? Решение. За первый час второй путник отстанет от первого на 4 – 10/3 = 2/3 версты. За второй час еще на 2/3 версты, за третий час еще на 2/3 версты и т.д. Путники сойдутся вместе опять, когда отставание сравняется с длиной пути вокруг города , то есть станет равным 15 верстам. На это понадобится 15: 2/3 = 22 ½ час. Первый путник за это же время пройдет 4 * 22 ½ = 90 верст и обойдет 90: 15=6 раз вокруг города. Второй путник пройдет на 15 верст меньше и сделает на один обход меньше. Таким образом, путники сойдутся опять через 22 ½ часа. Первый из них обойдет вокруг города 6 раз, второй 5 раз.

Задача 51. Магницкого Л.Ф. Деревня. Прохожий, догнавший другого, спросил: «Как далеко до деревни, которая у нас впереди?». Отвечал другой прохожий: « Расстояние от той деревни, от которой ты идешь, равно третьей части всего расстояния между деревнями, а если еще пройдешь 2 версты, тогда будешь ровно посередине между деревнями». Сколько верст осталось еще идти первому прохожему? Решение. До середины расстояния между деревнями первому прохожему нужно идти 2 версты, и это составляет 1/2 - 1/3 = 1/6 часть всего расстояния между деревнями. Поэтому расстояние между деревнями равно 12 верстам, к моменту встречи первый прохожий прошел 1/3 · 12 =4 версты и осталось ему идти еще 8 верст.

Задача 52. Магницкого Л.Ф. Один путник идет от города до дома 17 дней, другой то же расстояние от дома до города за 20 дней. Оба вышли в один и тот же час и из своих мест. Через сколько дней они встретятся? Решение. Обозначим весь путь за 1, тогда 1:( 1/17 + 1/20 ) = 1 : 37/340 = 340 / 37 = 9 + 7 / 37 Ответ: 9 +7/37 дней --Bookworm ID 213 15:30, 6 ноября 2008 (UZT)

Шоу "модель" ID_278

Задача из Вьетнама.Для кормления 100 буйволов заготовили 100 охапок сена. Стоящий молодой буйвол съедает 5 охапок сена. Лежащий молодой буйвол - 3 охапки сена. Старые буйволы втроём съедают 1 охапку сена. Сколько молодых буйволов стоят, сколько лежат и сколько буйволов старых?

Решение: Пусть x - число стоящих, y - число лежащих молодых буйволов и z - число старых буйволов. Тогда x+y+z=100, 5x+3y+z/3=100,y=25-7x/4. Так как x и y натуральные числа, то последнее равенство выполняется только при x=4,8,12. Задача допускает следующие решения x=4,y=18,z=78; 8, y=11, z=81; x=12, y=4, z=84.

Задача Шен Кана. Три снопа хорошего урожая, 2 снопа среднего урожая и 1 сноп плохого дают 39 доу (китайская мера) зерна. Два снопа хорошего урожая, 3 снопа среднего и 1 сноп плохого дают 34 доу. Один сноп хорошего, 2 снопа среднего и 3 снопа плохого урожая дают 36 доу зерна. Сколько доу зерна даёт 1 сноп хорошего, 1 сноп среднего и 1 сноп плохого урожая?

Решение:Пусть сноп хорошего урожая даёт x - доу зерна, среднего - y доу, плохого - z доу. Тогда 3x+2y+z=36, 2x+3y+z=34, x+2y+3z=36, откуда x=9,25 y=4,25 z=2,75.

Задача греческого математика Митродора.Царская корона имеет массу 60 мин (1 мина=100 драхм=1/60 таланта) и отлита из сплава золота, меди, свинца и железа. На золото и медь приходится 3/4, на золото и свинец - 2/3, на золото и железо - 3/5 массы короны. Сколько мин золота, меди, свинца и железа в царской короне?

Решение:Предположим, что на отливку короны пошло x мин золота, y мин меди, z мин свинца и f мин железа. Тогда x+y+z+f=60,(1). x+y=2/3*60=40,(2). x+z=3/4*60=45,(3). x+f=3/5*60=36,(4). Складывая уравнения (2),(3),(4), получаем 3x+y+z+f=121, вычитая из последнего уравнения уравнение (1), находим 2x=61,x=30,5. Значит y=9,5 z=14,5 f=5,5.Итак, 30,5 мин золота, 9,5 мин меди, 14,5 мин свинца и 5,5 мин железа.

Участник:Шоу "модель" ID_278--Шоу "модель" 16:44, 6 ноября 2008 (UZT)

--Bookworm ID 213 16:53, 7 ноября 2008 (UZT)

Задача №53. Задача французского автора Ж. Озанама (XVII в.)

Трое хотят купить дом за 24000 ливров. они условились, что первый даст половину, второй одну треть, а третий оставшуюся часть. Сколько денег даст каждый?

Решение:

1) Найдем, сколько денег даст первый человек: 24000*0,5=12000 (ливров) 2) Найдем количество денег, которое даст второй человек: 24000*1/3=8000 (ливров) 3) Найдем последнюю сумму денег: 24000–12000–8000=4000 (ливров) Ответ: I – 12000 ливров, II – 8000 ливров, III – 4000 ливров.

Задача№54. Задача из тракта «Математика в девяти книгах».

Сообща покупают вещь. Если каждый человек внесет по 8, то избыток (равен) 3. Если каждый человек внесет по 7, то недостаток (равен) 4. Спрашивается количество людей и стоимость вещи.

Решение:

пусть х – количество людей, тогда получим уравнение: 8х – 3=7х+4 Решая уравнение получим, что х=7. тогда стоимость вещи равна 8·7 – 3=53

Ответ: 7 человек, стоимость вещи 53.

Задача №55. Задача из тракта «Математика в девяти книгах».Имеется 5 воробьев и 6 ласточек, их взвесили на весах. вес всех воробьев тяжелее веса всех ласточек. если переместить 1 ласточку и 1 воробья, то вес будет как раз одинаковым. общий вес ласточек и воробьев 1 цзинь. Спрашивается, сколько весят ласточка и воробей.

Решение:

Обозначим за х вес одного воробья и за у вес одной ласточки. Получим систему из двух уравнений: 4х + у = 5у + х и 5х + 6 у = 1 . Знаем, что 5х > 6 у . Решая данные уравнения, имеем х = 2 /19 , у = 3/38 Ответ: вес воробья 2/ 19 цзинь , вес ласточки 3/ 38 цзиня.

Задача 56. Задача Алькуина.

Разделить сто мер пшеницы между сто лицами так , чтобы каждый мужчина получил три , каждая женщина два , а каждое дитя ½ меры. Сколько мужчин , женщин и детей?

Решение.

Составим систему неопределенных уравнений: х+у+с= 100 и 3х+2у+1/2с =100 , где х,у,с- натуральные числа ( мужчины , женщины, дети). Решая данную систему , получим уравнение 2у + 5с= 400. То есть , х= 11, у = 15, с = 74.

--Bookworm ID 213 16:53, 7 ноября 2008 (UZT)

Задачи команды ЛАДА-ВЕКТОР ID_279

Задача № 25

(Анания из Ширака, армянский математик VII века.)

В городе Афинах был водоём, в который проведены 3 трубы. Одна из труб может наполнить водоём в один час, другая, более тонкая, в два часа, третья, ещё более тонкая ,в три часа. Итак, узнай, в какую часть часа все три трубы вместе наполняют бассейн.

Решение:

В 6/11 часа. За 6 ч первая труба наполнит 6 таких водоёмов, вторая -3, а третья-2, всего 11 водоёмов. Значит, 3 трубы вместе наполнят один водоём за 6/11 часа.

Ответ: 6/11 часа.

Задача №26

Задача Адама Ризе ( XVI в.)

26 персон издержали вместе 88 марок, причём мужчина издерживал по 6 марок, женщина - по 4, девушка – по 2. Сколько было мужчин , женщин и девушек?

Решение:

Пусть было m мужчин, g женщин, тогда девушек было 26 - m-g. По условию задачи составим уравнение и упростим его:

6m+4g+2(26-m-g)=88 (6),

2m +g=18 (7).

Так как g делится на 2, подставим g = 2 g₁ (g₁ – натуральное число) в уравнении (7) и упростим его: m + g₁ =9 (8).

Уравнение (8) имеет 8 решений (m;g 1) в натуральных числах(1;8), (2;7), (3;6), (4;5), (5;4), (6;3), (7;2), (8;1). Уравнение (6) тоже имеет 8 решений (m;g) : (1;16), (2;14), (3;12), (4;10), (5;8), (6;6), (7;4), (8;2). Следовательно, задача имеет 8 решений: мужчин, женщин и девушек было 1, 16, 9, или 2, 14, 10, или 3, 12, 11, или 4,10,12, или 5, 8, 13, или 6,6, 14, или 7,4,15, или 8,2, 16.

Задача № 27

Задача Д.Пойа

Торговец продает орехи двух сортов: одни по 90 центов, и другие по 60 центов за килограмм. Он хочет получить 50 кг смеси по 72 цента за килограмм. Сколько для этого потребуется орехов каждого сорта?

Решение:

Пусть было x кг орехов первого сорта и y кг орехов второго сорта, тогда выполняются два равенства:

x+y=50,

90x+60y=3600.

Имеем:

(система)

х + у = 50,

3х + 2у = 120

Для решения систем двух уравнений с двумя переменными применяют один из двух основных способов решения.

1)Способ подстановки.

Выразим y через x из первого уравнения:y=50-x Подставим выражение 50-x во второе уравнение вместо y: 3x +2(50-x)=120, x=20 Теперь найдем y: y=50-20=30.

2)Способ сложения.

Умножим правую и левую части первого уравнения системы (1) на-2 и сложим почленно полученные уравнения:

(система)

- 2х – 2у = - 100,

3х+2у=120.

(система)

х=20,

у=30.

Ответ:20кг первого и 30кг второго сорта.

--Лада-Вектор ID 279 00:12, 9 ноября 2008 (UZT)

Совокупность "жареных семечек"ID-224

Из «Введения в анализ бесконечных», т.1, Л. Эйлер

Задача №40

Доказать, что логарифмы двух чисел в любой системе сохраняют одно и то же отношение.

Решение.

(a +blgx)lgx = lgc, пусть lgx = y, тогда by^2 + by – lgc = 0. Найдя y, находим х.

Задача №41

Пусть к концу каждого века число людей удваивается; требуется найти годовой прирост.

Решение.

Если предположим, что число людей возрастает ежегодно на 1/х свою часть, и, притом вначале число людей было равно n, то по истечении 100 лет, это число будет равно [((1+х)/х)^100]*n.

Это должно быть равно 2nи тогда (1+x)/x = 2^1/100, логарифмируем: lg(1+x)/x = 1/100, lg2 = 0,0030103, отсюда (1+х)/х = 10069555/10000000, поэтому х ≈144.

Итак, достаточно ежегодного прироста людей на 1/144 часть.

Задача №42

Пусть число людей увеличивается ежегодно на 1/100 свою часть; спрашивается, через сколько лет число людей удесятериться.

Решение.

Положим, что это наступит через х лет, причем число людей вначале было равно n;

стало быть по истечении х лет оно будет равно [(101/100)^x]*n, а так как оно должно равняться 10n, то

(101/100)^x = 10, xlg(101/100) = lg10, x = lg10/(lg101-lg100) = 1/(lg101-2), x≈231.

Итак, через 231 год число людей, если ежегодное приращение составляет только 1/100 часть, станет больше в 10 раз, отсюда

через 462 года оно станет в 100 раз, а через 693 года в 1000 раз больше.

Задача №43. Задача Ж. Озанама.

Семеро друзей собрались к обеду, но между ними возник спор, кому с кем садиться. Чтобы прекратить пререкания, кто-то из присутствующих предложил всем сесть за стол как придется, но с условием, чтобы в следующие дни обедать вместе, причем каждый раз садиться по разному, до тех пор, пока не будут испробованы все комбинации.

Спрашивается, сколько раз придется им обедать вместе для этой цели?

Решение.

Задача №44. Середина 14 века. Задача Нарайана.

Подсчитать стадо коров и телок, происходящее от одной коровы за 20 лет, по условию корова в начале каждого года рожает телку, а телки дают такое же потомство, достигнув трех лет.

Решение.

В начале 1-го года стадо состояло из 2-х животных, в начале 2-го –из 3-х, затем из 4 и 6.

Начиная с 4-го года численность стада можно выразить рекуррентным соотношением:

S(k) = S(k-1)+S(k-3).

С помощью соотношения последовательно вычисляем S(20) =2745.

Задача №45 Задача о кроликах или числа Фибоначчи

В 1202 году итальянский купец Леонардо из Пизы (1180—1240), более известный под прозвищем Фибоначчи, один из самых значительных математиков средневековья, сформулировал такую задачу:

"Некто поместил пару кроликов в некоем месте, огороженном со всех сторон стеной, чтобы узнать, сколько пар кроликов родится при этом в течение года, если природа кроликов такова, что через месяц пара кроликов производит на свет другую пару, а рождают кролики со второго месяца после своего рождения."

Рост численности кроликов можно проследить на схеме, выполненной в виде

Задача №46. Китай. «Математический трактат о чжоу-би»

В центре бассейна со стороной 1 чжан = 10 чи растет камыш, выступающий над водой на 1 чи. Оттянутый камыш достигает берега. Какова глубина воды?

Решение.

Сторона бассейна 2а, камыш выступает на высоту h, глубина х.

По теореме Пифагора (х+h)^2 – x^2 = a^2.

(x+1)^2-x^2 = 5^2, 2x+1=25, x=12 (чи)

«Математика в девяти книгах» («Цзю чжан суань шу»

Авторы неизвестны. Лю Хуэй, комментировавший «Математику» в 3 в. , сообщает, что она была составлена по более ранним источникам видным чиновником финансовой службы Чжан Цанем (умер в 152 г. до н.э.)

Задача №47.

В бочке в 10 доу есть неизвестное количество пшена. Бочка дополнена неочищенным просом, и если последнее очистить, то всего получится 7 доу пшена.

Решение.

Запишем уравнение.

х +3/5(10-х)=7 (3/5 – коэффициент перехода от проса к пшену из книги 2 «Математики»)

х = 2,5.

Задача №48.

Наверху стены в 90 цуней растет тыква, стебель которой за день вырастает на 7, внизу растет кабачок, стебель которого вырастает за день на 10. Когда они встретятся?

Решение.

Запишем уравнение (7+10)х = 90.,

х = 90/17=5+5/17 дней.

Задача №49.

Из 3 снопов хорошего урожая, 2 снопов среднего урожая и 1 снопа плохого урожая получили 39 доу. Из двух снопов хорошего урожая, 3 снопов среднего урожая и 1 снопа плохого урожая получили 34 доу. Из 1 снопа хорошего урожая, 2 снопов среднего урожая и 3 снопов плохого урожая получили 26 доу.

Спрашивается, сколько получили из каждого снопа хорошего, среднего и плохого урожая?

Решение.

урожай

Хороший урожай Средний урожай Плохой урожай Весь урожай В 1-м снопе х доу В 1-м снопе y доу В 1-м снопе z доу 3 снопа 2 снопа 1 сноп 39 доу 2 снопа 3 снопа 1сноп 34 доу 1сноп 2 снопа 3 снопа 26 доу

3x+2y+z=39, 2x+3y+z=34, x+2y+3z=26.

x-y=5, x=5+y.

z=34-2(5+y)-3y, z=24-5y.

5+y+2y+(24-5y)*3=26, -12y=26 -77, y=51/12,

y=4+1/4,

X=9+1/4,

z = 2+3/4

Ответ.

Из одного снопа хорошего урожая получается 9,25 доу, из одного снопа среднего урожая получается 4,25 доу, из одного снопа плохого урожая получается 2,75 доу.

Задача №50.

2 снопам хорошего урожая, 3 снопам среднего урожая, 4 снопам плохого урожая не хватает до 1 доу соответственно по 1 снопу среднего урожая, плохого урожая, хорошего урожая.

Спрашивается, сколько получили из каждого снопа хорошего, среднего и плохого урожая?

Решение.

В 1-м снопе хорошего х доу, в 1-м снопе среднего y доу, в 1-м снопе плохого z доу

2х+у =1, 3у+z=1, 4z+x=1.

Y=1-2x, z=1-3y, 4-12(1-2x)+x=1, 25x=9,

x=0,36, y=0,28, z=0,16.

Ответ.

Из одного снопа хорошего урожая получается 0,36 доу, из одного снопа среднего урожая получается 0,28 доу, из одного снопа плохого урожая получается 0,16 доу.

--"Жареные семечки" 23:31, 9 ноября 2008 (UZT)

Копилка знаменитых задач продолжение 6

Версия 22:44, 9 ноября 2008

Задачи участников ДООМ

Совокупность "жареных семечек"ID-224

Просмотры

Личные инструменты

Навигация

Поиск

Инструменты

наши друзья

@@ Строка 659: / Строка 659: @@
 == '''Совокупность "жареных семечек"ID-224''' ==
-Из «Введения в анализ бесконечных», т.1, Л. Эйлер
+'''Из «Введения в анализ бесконечных», т.1, Л. Эйлер'''
-Задача №40
+'''Задача №40'''
 Доказать, что логарифмы двух чисел в любой системе сохраняют одно и то же  отношение.
 Решение.
 (a +blgx)lgx = lgc, пусть lgx = y, тогда by^2 + by – lgc = 0. Найдя y, находим х.
-Задача №41
+'''Задача №41'''
 Пусть к концу  каждого века число людей удваивается; требуется найти годовой прирост.
 Решение.
-Если предположим, что число людей возрастает ежегодно на 1/х свою часть, и, притом вначале число людей было равно n, то по истечении 100 лет,  это число будет равно [((1+х)/х)^100]*n. Это должно быть равно 2nи тогда (1+x)/x = 2^1/100, логарифмируем: lg(1+x)/x = 1/100, lg2 = 0,0030103, отсюда (1+х)/х = 10069555/10000000, поэтому х ≈144.
+Если предположим, что число людей возрастает ежегодно на 1/х свою часть, и, притом вначале число людей было равно n, то по истечении 100 лет,  это число будет равно [((1+х)/х)^100]*n.
+Это должно быть равно 2nи тогда (1+x)/x = 2^1/100, логарифмируем: lg(1+x)/x = 1/100, lg2 = 0,0030103, отсюда (1+х)/х = 10069555/10000000, поэтому х ≈144.
 Итак, достаточно ежегодного прироста людей на 1/144 часть.
-Задача №42
+'''Задача №42'''
 Пусть число людей увеличивается ежегодно на 1/100 свою часть; спрашивается, через сколько лет число людей удесятериться.
 Решение.
-Положим, что это наступит через х лет, причем число людей вначале было равно n; стало быть по истечении х лет оно будет равно [(101/100)^x]*n, а так как оно должно равняться 10n, то (101/100)^x = 10, xlg(101/100) = lg10, x = lg10/(lg101-lg100) = 1/(lg101-2), x≈231.
-Итак, через 231 год число людей, если ежегодное приращение составляет только 1/100 часть, станет больше в 10 раз, отсюда через 462 года оно станет в 100 раз, а через 693 года в 1000 раз больше.
+Положим, что это наступит через х лет, причем число людей вначале было равно n;
-Задача №43. Задача Ж. Озанама.
-Семеро друзей собрались к обеду, но между ними возник спор, кому с кем садиться. Чтобы прекратить пререкания, кто-то из присутствующих предложил всем сесть за стол как придется, но с условием, чтобы в следующие дни обедать вместе, причем каждый раз садиться по разному,  до тех пор, пока не будут испробованы все комбинации. Спрашивается, сколько раз придется им обедать вместе для этой цели?
+стало быть по истечении х лет оно будет равно [(101/100)^x]*n, а так как оно должно равняться 10n, то
+(101/100)^x = 10, xlg(101/100) = lg10, x = lg10/(lg101-lg100) = 1/(lg101-2), x≈231.
+Итак, через 231 год число людей, если ежегодное приращение составляет только 1/100 часть, станет больше в 10 раз, отсюда
+через 462 года оно станет в 100 раз, а через 693 года в 1000 раз больше.
+'''Задача №43. Задача Ж. Озанама.'''
+Семеро друзей собрались к обеду, но между ними возник спор, кому с кем садиться. Чтобы прекратить пререкания, кто-то из присутствующих предложил всем сесть за стол как придется, но с условием, чтобы в следующие дни обедать вместе, причем каждый раз садиться по разному,  до тех пор, пока не будут испробованы все комбинации.
+Спрашивается, сколько раз придется им обедать вместе для этой цели?
 Решение.
-Задача №44. Середина 14 века. Задача Нарайана.
+'''Задача №44. Середина 14 века. Задача Нарайана.'''
 Подсчитать стадо коров и телок, происходящее от одной коровы за 20 лет, по условию корова в начале каждого года рожает телку, а телки дают такое же потомство, достигнув трех лет.
-Решение.
-В начале 1-го года стадо состояло из 2-х животных, в начале 2-го –из 3-х, затем из 4 и 6. Начиная с 4-го года численность стада можно выразить рекуррентным соотношением:
-S(k) = S(k-1)+S(k-3).  С помощью соотношения последовательно вычисляем S(20) =2745.
-Задача №45 Задача о кроликах или числа Фибоначчи
-В 1202 году итальянский купец Леонардо из Пизы (1180—1240), более известный под прозвищем Фибоначчи, один из самых значительных математиков средневековья, сформулировал такую задачу:
-Некто поместил пару кроликов в некоем месте, огороженном со всех сторон стеной, чтобы узнать, сколько пар кроликов родится при этом в течение года, если природа кроликов такова, что через месяц пара кроликов производит на свет другую пару, а рождают кролики со второго месяца после своего рождения.
-Рост численности кроликов можно проследить на схеме, выполненной в виде
+'''Решение.'''
+В начале 1-го года стадо состояло из 2-х животных, в начале 2-го –из 3-х, затем из 4 и 6.
+Начиная с 4-го года численность стада можно выразить рекуррентным соотношением:
+S(k) = S(k-1)+S(k-3).
+С помощью соотношения последовательно вычисляем S(20) =2745.
+'''Задача №45 Задача о кроликах или числа Фибоначчи'''
+В 1202 году итальянский купец Леонардо из Пизы (1180—1240), более известный под прозвищем Фибоначчи, один из самых значительных математиков средневековья, сформулировал такую задачу:
+"Некто поместил пару кроликов в некоем месте, огороженном со всех сторон стеной, чтобы узнать, сколько пар кроликов родится при этом в течение года, если природа кроликов такова, что через месяц пара кроликов производит на свет другую пару, а рождают кролики со второго месяца после своего рождения."
+Рост численности кроликов можно проследить на схеме, выполненной в виде
+[[Изображение:Example.jpg]]
+'''Задача №46. Китай. «Математический трактат о чжоу-би»'''
-Задача №46. Китай. «Математический трактат о чжоу-би»
 В центре бассейна со стороной 1 чжан = 10 чи растет камыш, выступающий над водой на 1 чи. Оттянутый камыш достигает берега. Какова глубина воды?
-Решение.
+Решение.
 Сторона бассейна 2а, камыш выступает на высоту h, глубина х.
-По теореме Пифагора (х+h)^2 – x^2 = a^2.  (x+1)^2-x^2 = 5^2,  2x+1=25, x=12 (чи)
+[[Изображение:Example.jpg]]
-«Математика в девяти книгах» («Цзю чжан суань шу» Авторы неизвестны. Лю Хуэй, комментировавший «Математику» в 3 в. , сообщает, что она была составлена по более ранним источникам видным чиновником финансовой службы Чжан Цанем (умер в 152 г. До н.э.)
-Задача №47.
+По теореме Пифагора (х+h)^2 – x^2 = a^2.
+(x+1)^2-x^2 = 5^2,  2x+1=25, x=12 (чи)
+'''«Математика в девяти книгах» («Цзю чжан суань шу»'''
+Авторы неизвестны. Лю Хуэй, комментировавший «Математику» в 3 в. , сообщает, что она была составлена по более ранним источникам видным чиновником финансовой службы Чжан Цанем (умер в 152 г. до н.э.)
+'''Задача №47.'''
 В бочке в 10 доу есть неизвестное количество пшена. Бочка дополнена неочищенным просом, и если последнее очистить, то всего получится 7 доу пшена.
 Решение.
 Запишем уравнение.
 х +3/5(10-х)=7 (3/5 – коэффициент перехода от проса к пшену из книги 2 «Математики»)
 х = 2,5.
-Задача №48.
+'''Задача №48.'''
 Наверху стены в 90 цуней растет тыква, стебель которой за день вырастает на 7, внизу растет кабачок, стебель которого вырастает за день на 10. Когда они встретятся?
+Решение.
+Запишем уравнение (7+10)х = 90.,
+х = 90/17=5+5/17 дней.
+'''Задача №49.'''
+Из 3 снопов хорошего урожая, 2 снопов среднего урожая и 1 снопа плохого урожая получили 39 доу. Из двух снопов хорошего урожая, 3 снопов среднего урожая и 1 снопа плохого урожая получили 34 доу. Из 1 снопа хорошего урожая, 2 снопов среднего урожая и 3 снопов плохого урожая получили 26 доу.
+Спрашивается, сколько получили из каждого снопа хорошего, среднего и плохого урожая?
 Решение.
-Запишем уравнение (7+10)х = 90., х = 90/17=5+5/17 дней.
+ урожай
-Задача №49.
-Из 3 снопов хорошего урожая, 2 снопов среднего урожая и 1 снопа плохого урожая получили 39 доу. Из двух снопов хорошего урожая, 3 снопов среднего урожая и 1 снопа плохого урожая получили 34 доу. Из 1 снопа хорошего урожая, 2 снопов среднего урожая и 3 снопов плохого урожая получили 26 доу. Спрашивается, сколько получили из каждого снопа хорошего, среднего и плохого урожая?
-Решение. урожай
 Хороший урожай 	Средний урожай	Плохой урожай	Весь урожай
 В 1-м снопе х доу	В 1-м снопе y доу	В 1-м снопе z доу
@@ Строка 715: / Строка 784: @@
 x+2y+z=39, 2x+3y+z=34, x+2y+3z=26.
 x-y=5, x=5+y.
 z=34-2(5+y)-3y, z=24-5y.
-+y+2y+(24-5y)*3=26, -12y=26 -77, y=51/12, y=4+1/4,
-X=9+1/4, z = 2+3/4
++y+2y+(24-5y)*3=26, -12y=26 -77, y=51/12,
-Ответ. Из одного снопа хорошего урожая получается 9,25 доу, из одного снопа среднего урожая получается 4,25 доу, из одного снопа плохого урожая получается 2,75 доу.
-Задача №50.
+y=4+1/4,
-снопам хорошего урожая, 3 снопам среднего урожая, 4 снопам плохого урожая не хватает до 1 доу соответственно по 1 снопу среднего урожая, плохого урожая, хорошего урожая. Спрашивается, сколько получили из каждого снопа хорошего, среднего и плохого урожая?
+X=9+1/4,
+z = 2+3/4
+Ответ.
+Из одного снопа хорошего урожая получается 9,25 доу, из одного снопа среднего урожая получается 4,25 доу, из одного снопа плохого урожая получается 2,75 доу.
+'''Задача №50.'''
+снопам хорошего урожая, 3 снопам среднего урожая, 4 снопам плохого урожая не хватает до 1 доу соответственно по 1 снопу среднего урожая, плохого урожая, хорошего урожая.
+Спрашивается, сколько получили из каждого снопа хорошего, среднего и плохого урожая?
 Решение.
 В 1-м снопе хорошего х доу, в 1-м снопе среднего y доу, в 1-м снопе плохого z доу
 х+у =1, 3у+z=1, 4z+x=1.
-Y=1-2x, z=1-3y, 4-12(1-2x)+x=1, 25x=9, x=0,36, y=0,28, z=0,16.
-Ответ. Из одного снопа хорошего урожая получается 0,36 доу, из одного снопа среднего урожая получается 0,28 доу, из одного снопа плохого урожая получается 0,16 доу.
+Y=1-2x, z=1-3y, 4-12(1-2x)+x=1, 25x=9,
+x=0,36, y=0,28, z=0,16.
+Ответ.
+Из одного снопа хорошего урожая получается 0,36 доу, из одного снопа среднего урожая получается 0,28 доу, из одного снопа плохого урожая получается 0,16 доу.
 --[[Участник:Совокупность "жареных семечек"ID-224|&quot;Жареные семечки&quot;]] 23:31, 9 ноября 2008 (UZT)