Семинар ДООМ: Деление угла циркулем и линейкой
| Строка 60: | Строка 60: | ||
''Ответ: построение прямого угла'' | ''Ответ: построение прямого угла'' | ||
| + | |||
[[Изображение: СС1.JPG]] | [[Изображение: СС1.JPG]] | ||
| Строка 69: | Строка 70: | ||
''Ответ: построение серединного перпендикуляра РН к АВ'' | ''Ответ: построение серединного перпендикуляра РН к АВ'' | ||
| + | |||
[[Изображение: СС2.JPG]] | [[Изображение: СС2.JPG]] | ||
| Строка 79: | Строка 81: | ||
''Ответ: построение биссектрисы угла'' | ''Ответ: построение биссектрисы угла'' | ||
| + | |||
[[Изображение: СС3.JPG]] | [[Изображение: СС3.JPG]] | ||
| Строка 88: | Строка 91: | ||
''Ответ: построение равностороннего треугольника'' | ''Ответ: построение равностороннего треугольника'' | ||
| + | |||
[[Изображение: СС4.JPG]] | [[Изображение: СС4.JPG]] | ||
| Строка 115: | Строка 119: | ||
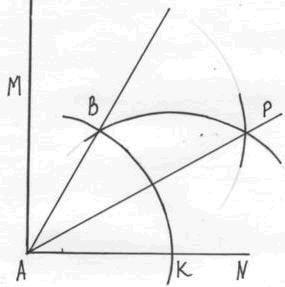
'''Задача 1:''' Трисекция прямого угла. | '''Задача 1:''' Трисекция прямого угла. | ||
| + | |||
[[Изображение: СС5.JPG]] | [[Изображение: СС5.JPG]] | ||
| + | |||
Пусть требуется разделить на три равные части прямой угол MAN. Откладываем на луче АN произвольный отрезок АК, на котором строим равносторонний треугольник AКB. Так как угол КAB равен 60 градусов, то угол МАВ = 30 градусов. Построим биссектрису угла КАВ, получаем искомое деление прямого угла MAN на три равных угла. | Пусть требуется разделить на три равные части прямой угол MAN. Откладываем на луче АN произвольный отрезок АК, на котором строим равносторонний треугольник AКB. Так как угол КAB равен 60 градусов, то угол МАВ = 30 градусов. Построим биссектрису угла КАВ, получаем искомое деление прямого угла MAN на три равных угла. | ||
| Строка 162: | Строка 168: | ||
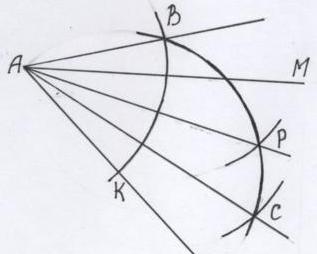
'''Задача 1:''' Трисекция угла в 45 градусов. | '''Задача 1:''' Трисекция угла в 45 градусов. | ||
| − | + | ||
''Решение'' данной задачи сводится к построению равностороннего треугольника. Пусть требуется разделить на три равные части угол MAN=45 градусов. Откладываем на луче АN произвольный отрезок АК, на котором строим равносторонний треугольник AКB в одной полуплоскости с точкой М относительно прямой АК. Строим биссектрису АР угла КАВ, затем биссектрису АС угла РАК и получаем искомое деление угла MAN на три равных угла углы МАР=РАС=САК=15 градусов. | ''Решение'' данной задачи сводится к построению равностороннего треугольника. Пусть требуется разделить на три равные части угол MAN=45 градусов. Откладываем на луче АN произвольный отрезок АК, на котором строим равносторонний треугольник AКB в одной полуплоскости с точкой М относительно прямой АК. Строим биссектрису АР угла КАВ, затем биссектрису АС угла РАК и получаем искомое деление угла MAN на три равных угла углы МАР=РАС=САК=15 градусов. | ||
| Строка 177: | Строка 183: | ||
'''Задача 3:''' Разделить угол на 4 равных угла. | '''Задача 3:''' Разделить угол на 4 равных угла. | ||
| − | [[Изображение: | + | |
| + | [[Изображение: СС6.JPG]] | ||
| + | |||
''Решение:'' Разделить угол АВС на 4 равных угла. Строим биссектрису ВК угла АВС, получаем углы АВК= СВК=угол АВС:2. Строим биссектрисы ВР и ВМ углов АВК и CDR соответственно. Получаем: углы АВР=РВК=МВК=СВМ= угол АВК:2= угол АВС:4. | ''Решение:'' Разделить угол АВС на 4 равных угла. Строим биссектрису ВК угла АВС, получаем углы АВК= СВК=угол АВС:2. Строим биссектрисы ВР и ВМ углов АВК и CDR соответственно. Получаем: углы АВР=РВК=МВК=СВМ= угол АВК:2= угол АВС:4. | ||
| Строка 233: | Строка 241: | ||
'''Приложение:''' | '''Приложение:''' | ||
| + | |||
[[Изображение: СС8.JPG]] | [[Изображение: СС8.JPG]] | ||
| + | |||
| + | [[Изображение: СС7.JPG]] | ||
'''Список литературы:''' | '''Список литературы:''' | ||
Версия 18:48, 19 ноября 2009
Задачи на построение циркулем и линейкой и сегодня считаются математически весьма интересными. Уже более ста лет это традиционный материал школьного курса геометрии. Одной из самых ценных сторон таких задач является то, что они развивают поисковые навыки решения практических проблем, приобщают к самостоятельным исследованиям, способствуют выработке конкретных геометрических представлений. Задачи на построение вызывают интерес, способствуют активизации мыслительной и познавательной деятельности. При их решении активно используются знания о свойствах фигур, совершенствуются навыки геометрических построений. В результате развиваются конструктивные способ-ности, что является одной из целей изучения геометрии.
Круг задач, рассматриваемых в геометрии, очень широк. Среди них особое место занимают задачи на построение, которые способствуют развитию определенности, последовательности и обоснованности мышления. На этих задачах можно научиться таким методам познания, как анализ и синтез.
Тема урока: Деление угла циркулем и линейкой.
Класс: 7 (углубленное изучение)
Тип урока: урок изучения нового материала. Методы и приёмы ведения урока:
- фронтальная работа с классом;
- закрепление: работа учащихся в парах по карточкам.
Цели урока:
Обучающая: обеспечить усвоение нового материала, проверка знания учащимися фактического материала по теме «Задачи на построение циркулем и линейкой»; умений учащихся самостоятельно применять знания в измененных нестандартных условиях.
Развивающая: Развивать мышление учащихся при решении задач, выходящих за рамки школьного курса; развивать умение анализировать, сравнивать, делать выводы; развивать память учащихся.
Воспитательная: воспитание у учащихся интереса к предмету, доброжелательности, умения работать в коллективе и в парах.
Оборудование:
- интерактивная доска;
- рабочая карточка для каждого ученика (Приложение);
- презентация для интерактивной доски.
Задачи урока:
- повторить основные построения циркулем и линейкой;
- рассмотреть возможность деления угла на равных углов;
- отработать навык построения биссектрисы угла, равностороннего треугольника.
Ход урока
I. Организационный момент
II. Постановка цели и задач урока.
Ребята должны
знать: стандартные построения циркулем и линейкой,
уметь: 1) строить биссектрису угла, равносторонний треугольник; 2) применять стандартные построения при решении задач на деление угла циркулем и линейкой.
III. Актуализация опорных знаний
На экране появляются слайды, на которых последовательность шагов. Ученикам необходимо определить какую задачу на построение описывает данная последовательность шагов.
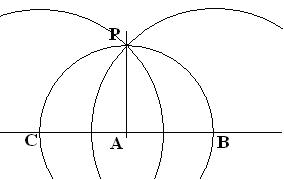
Задание 1:
- АВ – прямая.
- Проведем окр.(А;АВ) С – точка пересечения окружности и прямой АВ.
- Проведем окр.(С;R) и окр.(В;R) Р – точка пересечения окружностей.
- Проведем СР.
Ответ: построение прямого угла
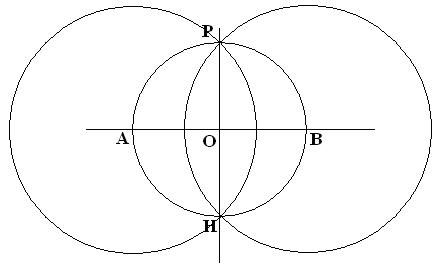
Задание 2:
- АВ – отрезок.
- Проведем окр.(А;R) и окр.(В;R) Р, Н – точки пересечения окружностей.
- Проведем РН, получим точку О на АВ.
Ответ: построение серединного перпендикуляра РН к АВ
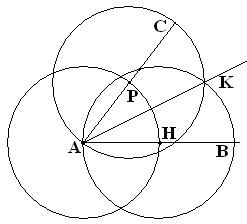
Задание 3:
- САВ
- Проведем окр.(А;R) Р, Н – точки пересечения окружности и сторон угла.
- Проведем окр.(Р;РН) и окр.(Н;РН) К – точка пересечения окружностей.
- Проведем АК.
Ответ: построение биссектрисы угла
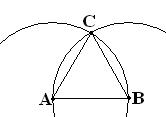
Задание 4:
- АВ – отрезок.
- Проведем окр.(А;АВ) и окр.(В;АВ) С – точка пересечения окружностей.
- Проведем АС и ВС
Ответ: построение равностороннего треугольника
IV. Изучение нового материала
Учитель: Сегодня нам необходимо определить всегда ли выполнимо «Деление данного угла на равных углов».
Учитель: Как вы считаете, какое стандартное построение позволит нам выполнить деление угла на 2, 4, 8, 16, … равных угла?
Ответ: Построение биссектрисы угла позволяет разделить любой угол на 2, 4, 8, … 2n равных углов. В каждом случае задача сводится к построению биссектрис полученных углов, что выполнимо всегда циркулем и линейкой. Например, разделить угол АВС на 4 равных угла. Строим биссектрису ВК угла АВС, получаем угол АВК= углу СВК= угол АВС:2. Строим биссектрисы ВР и ВМ углов АВК и CDR соответственно. Получаем: углы АВР= РВК= МВК= СВМ= АВК:2= АВС:4.
Учитель: Можно ли разделить произвольный угол на 3 равных угла?
Историческая справка. Можно дать задание ученикам подготовить небольшой доклад на тему трисекции угла. Трисекция угла. Искусство построения геометрических фигур при помощи циркуля и линейки было в высокой степени развито в Древней Греции. Знаменитой была в древности задача о трисекции угла (о разделении угла на три равные части с помощью циркуля и линейки). Любой угол невозможно разделить на три равных части с помощью только циркуля и линейки. Попытки решения задачи с помощью инструментов и средств были предприняты еще в V в. до н.э. Французский математик П. Ванцель в 1837г. первым строго доказал, что невозможно осуществить трисекцию циркулем и линейкой.
Задача о трисекции угла становится разрешимой и общем случае, если не ограничиваться в геометрических построениях одними только классическими инструментами, циркулем и линейкой. Так, например, Гиппий Элидский, знаменитый софист, живший около 420 г. до н.э., пользовался для трисекции угла квадратрисой. Александрийский математик Никомед (II в. до н.э.) решил задачу о трисекции угла с помощью одной кривой, названной конхоидой Никомеда, и дал описание прибора для черчения этой кривой. Интересное решение задачи о трисекции угла дал Архимед в своей книге «Леммы».
Задача о трисекции угла оказывается разрешимой и при некоторых других частных значениях угла: 90, 45, 135 (в градусах). Деление прямого угла на три равные части умели производить ещё пифагорейцы, основываясь на том, что в равностороннем треугольнике каждый угол равен 60 градусов.
Учитель: На интерактивной доске приведено решение задачи.
- Рассмотрите решение данной задачи.
- Определите основные построения.
- Докажите, что данные шаги приведут к необходимому результату.
Задача 1: Трисекция прямого угла.
Пусть требуется разделить на три равные части прямой угол MAN. Откладываем на луче АN произвольный отрезок АК, на котором строим равносторонний треугольник AКB. Так как угол КAB равен 60 градусов, то угол МАВ = 30 градусов. Построим биссектрису угла КАВ, получаем искомое деление прямого угла MAN на три равных угла.
Ответы:
2. Построение равностороннего треугольника, построение биссектрисы угла.
3. Доказательство: угол MAN=90 градусов. Треугольник AКB – равносторонний, угол КAB = 60 градусов. Значит, угол МАВ= угол MAN – угол КAB = 30 градусов. АР – биссектриса угла КАВ, значит угол КАР= углу РАВ=30 градусов. Получаем, что угол КАР=уголу РАВ=углу МАВ =30 градусов, т.е. искомое деление прямого угла MAN на три равных угла.
Учитель: В рабочей тетради выполните построение трисекции прямого угла, опи-сав все этапы «Построения». Обязательно написать «Доказательство».
Учитель: Какие углы всегда можно построить с помощью циркуля и линейки?
Ответ: углы: 60 градусов – угол в равностороннем треугольнике, 30 градусов – биссектриса угла в равностороннем треугольнике, 45 градусов – биссектриса прямого угла, 15 градусов – биссектриса угла 30 градусов, 90 градусов – перпендикуляр к прямой, 180 градусов – точка на прямой.
Учитель: Можно ли разделить произвольный угол на 5, 7, 11, … равных углов?
Учитель:Данная задача оказывается разрешимой при некоторых частных значениях угла. Например: циркулем и линейкой можно выполнить следующее построение (при условии, что заданные углы уже построены и их величина известна):
Задача 2: Разделить угол 66 градусов на 11 равных частей (при условии, что этот угол построен и его величина известна).
Решение: Т.к. 66 градусов: 11=6 градусов, то для решения этой задачи опять воспользуемся углом 60 градусов – равносторонним треугольником. При построении равностороннего треугольника получаем 66 градусов–60 градусов = 6 градусов, строим дважды по углу 6 градусов (60–6–6 = 48 градусов), затем делим угол 48 градусов на 8 равных углов (т.е. проводим биссектрисы). При этом получаем 11 углов по 6 градусов.
При рассмотрении данной задачи учитель задает наводящие вопросы и подводит ребят к решению задачи. Решение задачи записывается в рабочую тетрадь.
V. Физкультминутка
Учитель проводит с учащимися упражнения для расслабления глаз.
V. Закрепление изученного материала – самостоятельная работа в парах
Учитель: Каждый ученик получает карточку с задачами (Приложение 1). У учеников, сидящих за одной партой, одинаковый вариант заданий. Работу ученики выполняют в паре, но каждый оформляет решение на своей карточке.
Оценка за работу на карточке (учитель озвучивает перед началом работы):
«5» - за 3 правильно выполненные и оформленные задачи.
«4» - за 2 правильно выполненные и оформленные задачи или за 3 задачи с недочетами в оформлении.
«3» - за 1 правильно выполненную и оформленную задачу или за 2 задачи с недочетами в оформлении.
Решение задач самостоятельной работы:
Задача 1: Трисекция угла в 45 градусов.
Решение данной задачи сводится к построению равностороннего треугольника. Пусть требуется разделить на три равные части угол MAN=45 градусов. Откладываем на луче АN произвольный отрезок АК, на котором строим равносторонний треугольник AКB в одной полуплоскости с точкой М относительно прямой АК. Строим биссектрису АР угла КАВ, затем биссектрису АС угла РАК и получаем искомое деление угла MAN на три равных угла углы МАР=РАС=САК=15 градусов.
Доказательство: Т.к. треугольник АКВ – равносторонний, то угол КАВ=60 градусов. АР – биссектриса угла КАВ, значит углы ВАР= РАК=30 градусов и угол МАР=угол МАК– угол РАК = 45 градусов – 30 градусов = 15 градусов. АС – биссектриса угла РАК, значит углы РАС= САК=15 градусов. Значит, углы МАР=РАС=САК=15 градусов.
Задача 2 (1 вариант): Разделить угол 50 градусов на 10 равных углов.
Решение: Т.к. 50: 5=10, то для решения этой задачи воспользуемся углом 60 градусов – равносторонним треугольником. Получаем 1) 60–50 = 10 , 2) 50–10= 40, 3) 40: 4=10(в градусах).
Задача 2 (2 вариант): Разделить угол 720 на 6 равных углов.
Решение: Т.к. 72: 6=12, то для решения этой задачи воспользуемся углом 60 – равносторонним треугольником. Получаем 1) 72–60 = 12, 2) 60–12= 48, 3) 48: 4=12 (в градусах).
Задача 3: Разделить угол на 4 равных угла.
Решение: Разделить угол АВС на 4 равных угла. Строим биссектрису ВК угла АВС, получаем углы АВК= СВК=угол АВС:2. Строим биссектрисы ВР и ВМ углов АВК и CDR соответственно. Получаем: углы АВР=РВК=МВК=СВМ= угол АВК:2= угол АВС:4.
VI. Домашняя работа
Дома. Решить задачи:
1.Трисекция угла в 135 градусов.
2.Построить угол 53 градуса, если построен угол 104 градуса.
VII. Итог урока
Ответить на вопросы:
1.Всегда ли выполнима трисекция угла?
Только в некоторых частных случаях: 450, 900.
2.Что нового узнали на уроке?
Всегда можно построить циркулем и линейкой:
1) угла в n раз больше данного угла.
2) разделить любой угол на 2, 4, 8, … 2n равных углов.
3) углы: 60, 30, 45, 15, 90, 180 (в градусах).
4) можно разделить некоторые заданные углы на данное количество равных углов или построить угол необходимой величины.
3.Можно ли разделить произвольный угол на 5, 7, 11, … равных углов?
Нет. Только в некоторых частных случаях.
Домашняя работа:
Задача 1: Трисекция угла в 135 градусов.
Пусть требуется разделить на три равные части угол MAN=135 градусов. Т.к. 135:3 = 45, то из точки А строим перпендикуляр АК к прямой АМ. Затем строим биссектрису АР угла КАМ. При этом получаем искомое деление угла MAN на три равных угла углы КАN=КАР=РАМ=45 градусов.
Доказательство: Т.к. АК – перпендикуляр к прямой АМ, то угол КАМ=90 градусов, угол NАК= 135 градусов – 90 градусов = 45 градусов. АР – биссектриса угла КАМ, значит угол ВАР= углу РАК = 45 градусов. Значит, углы МАР=РАС=САК=45 градусов.
Задача 2: Построить угол 53 градуса, если построен угол 104 градуса.
При решении используем построения прямого угла, биссектрисы угла и угла 60 градусов.
Построение: 1) 104 градуса–90 градусов =14 градусов, 2) 14 градусов : 2 = 7 градусов, 3) строим 60 градусов и 60 градусов –7 градусов = 53 градуса.
Приложение:
Список литературы:
- Атанасян Л.С. Геометрия 7-9. М.: Просвещение, 2005. - 335 с.
- Далингер В.А. Планиметрические задачи на построение. Омск: Изд-во ОГПИ, 1999. - 78 с.
- Ильина Н.И. Геометрические построения на плоскости. М.: Школа - пресс, 1997. - 172 с.
- Манин И.Ю. О разрешимости задач на построение с помощью циркуля и линейки // Энциклопедия элементарной математики. М.: Физматгиз, 1963. Т. 4: Геометрия. С. 205-227.
- Погорелов А.В. Геометрия, 7–11. М.: Просвещение, 1992
- Прасолов В.В. Три классические задачи на построение. М.: Наука, 1992. 80 с.
- Энциклопедия для детей. Т. 11. Математика/Ред. коллегия: М.Аксенова, В.Володин и др. – М.: Аванта+, 2005.
- [1]
- [2]
- [3]