Семинар ДООМ урок геометрии на тему: "Ось симметрии"
(Новая: Участник:Тютерева Валентина Сергеевна команда Плюс_IDm045 '''Тема урока:''' "Ось симметрии" '''Цели:''' * да...) |
|||
| Строка 9: | Строка 9: | ||
'''ХОД УРОКА''' | '''ХОД УРОКА''' | ||
| + | |||
| + | '''Задание 1''' (3 мин). | ||
| + | – Возьмем лист бумаги, сложим его попалам и вырежем какую-нибудь фигурку. Теперь развернем лист и посмотрим на линию сгиба. | ||
| + | |||
| + | ''Вопрос:'' Какую функцию выполняет эта линия? | ||
| + | |||
| + | ''Предполагаемый ответ:'' Эта линия делит фигуру пополам. | ||
| + | |||
| + | ''Вопрос:'' Как расположены все точки фигуры на двух получившихся половинках? | ||
| + | |||
| + | ''Предполагаемый ответ:'' Все точки половинок находятся на равном расстоянии от линии сгиба и на одном уровне. | ||
| + | |||
| + | – Значит, линия сгиба делит фигурку пополам так, что 1 половинка является копией 2 половинки, т.е. эта линия непростая, она обладает замечательным свойством (все точки относительно ее находятся на одинаковом расстоянии), эта линия – ось симметрии. | ||
| + | |||
| + | '''Задание 2''' (2 мин). | ||
| + | |||
| + | – Вырезать снежинку, найти ось симметрии, охарактеризовать ее. | ||
| + | |||
| + | '''Задание 3''' (5 мин). | ||
| + | |||
| + | – Начертить в тетради окружность. | ||
| + | |||
| + | ''Вопрос:'' Определить, как проходит ось симметрии? | ||
| + | |||
| + | ''Предполагаемый ответ:'' По-разному. | ||
| + | |||
| + | ''Вопрос:'' Так сколько осей симметрии имеет окружность? | ||
| + | |||
| + | ''Предполагаемый ответ:'' Много. | ||
| + | |||
| + | – Правильно, окружность имеет множество осей симметрии. Такой же замечательной фигурой является шар (пространственная фигура) | ||
| + | |||
| + | ''Вопрос:'' Какие еще фигуры имеют не одну ось симметрии? | ||
| + | |||
| + | ''Предполагаемый ответ:'' Квадрат, прямоугольник, равносторонний треугольники. | ||
| + | |||
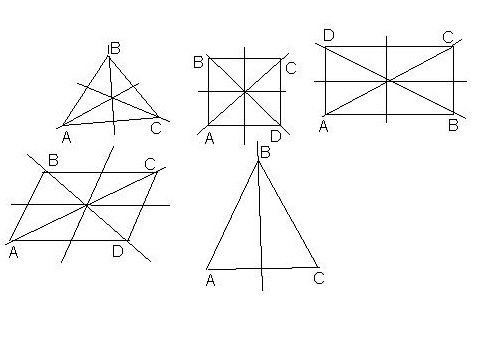
| + | Каждому ученику на парту раздается лист с заданиями. При работе с рисунком 3 ученики должны определить, сколько осей симметрии у квадрата, прямоугольника, равностороннего треугольника? | ||
| + | |||
| + | [[Изображение:GeomTWS4.jpg]] | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | [[Категория:Проект ДООМ 2009-2010]] | ||
Версия 14:44, 20 ноября 2009
Участник:Тютерева Валентина Сергеевна команда Плюс_IDm045
Тема урока: "Ось симметрии"
Цели:
- дать представление о симметрии, познакомить с основными видами симметрии на плоскости и в пространстве, выработать прочные навыки построения симметричных фигур;
- активизировать самостоятельную деятельность, развивать познавательную деятельность;
- воспитывать коммуникативность и интерес к предмету.
ХОД УРОКА
Задание 1 (3 мин). – Возьмем лист бумаги, сложим его попалам и вырежем какую-нибудь фигурку. Теперь развернем лист и посмотрим на линию сгиба.
Вопрос: Какую функцию выполняет эта линия?
Предполагаемый ответ: Эта линия делит фигуру пополам.
Вопрос: Как расположены все точки фигуры на двух получившихся половинках?
Предполагаемый ответ: Все точки половинок находятся на равном расстоянии от линии сгиба и на одном уровне.
– Значит, линия сгиба делит фигурку пополам так, что 1 половинка является копией 2 половинки, т.е. эта линия непростая, она обладает замечательным свойством (все точки относительно ее находятся на одинаковом расстоянии), эта линия – ось симметрии.
Задание 2 (2 мин).
– Вырезать снежинку, найти ось симметрии, охарактеризовать ее.
Задание 3 (5 мин).
– Начертить в тетради окружность.
Вопрос: Определить, как проходит ось симметрии?
Предполагаемый ответ: По-разному.
Вопрос: Так сколько осей симметрии имеет окружность?
Предполагаемый ответ: Много.
– Правильно, окружность имеет множество осей симметрии. Такой же замечательной фигурой является шар (пространственная фигура)
Вопрос: Какие еще фигуры имеют не одну ось симметрии?
Предполагаемый ответ: Квадрат, прямоугольник, равносторонний треугольники.
Каждому ученику на парту раздается лист с заданиями. При работе с рисунком 3 ученики должны определить, сколько осей симметрии у квадрата, прямоугольника, равностороннего треугольника?